4.2 Model Predictions
(a) Atmospheric flows trace an overall logarithmic spiral trajectory RoR1R2R3R4R5 with the quasiperiodic Penrose tiling pattern for the internal structure (Figure 6
2.5 Fivefold and Spiral Symmetry Associated with Fibonacci Sequence).(b) Conventional continuous periodogram power spectral analyses of such spiral trajectories will reveal a continuum of periodicities with progressive increase in phase.
(c) The broadband power spectrum will have embedded dominant wave-bands(RoOR1, R1OR2, R2OR3, R3OR4, R4OR5, etc.) the bandwidth increasing with period length(Figure 6). The peak periods En in the dominant wavebands will be given by the relation
En = TS(2+
t )t n (5)where
t is the golden mean equal to (1+Ö 5)/2 [=1.618] and Ts, the solar powered primary perturbation time period is the annual cycle (summer to winter) of solar heating in the present study of interannual variability. The most striking feature in climate variability on all time scales is the presence of sharp peaks superimposed on a continuous background(Ghil,1994 References ).(d) The ratio r/R also represents the increment d
q in phase angle q (Equation 3 and Figure 5) and therefore the phase angle q represents the variance. Hence, when the logarithmic spiral is resolved as an eddy continuum in conventional spectral analysis, the increment in wavelength is concomitant with increase in phase. The angular turning, in turn, is directly proportional to the variance( Equation 3) Such a result that increments in wavelength and phase angle are related is observed in quantum systems and has been named 'Berry's phase' (Berry , 1988;Simon et al.,1988;Maddox,1988b,1991; Samuel and Bhandari,1988; Kepler et al. 1991;Kepler,1992;Anandan,1992 References ). The relationship of angular turning of the spiral to intensity of fluctuations is seen in the tight coiling of the hurricane spiral cloud systems.(e) The overall logarithmic spiral flow structure is given by the relation
![]() (6)
(6)
where the constant k is the steady state fractional volume dilution of large eddy by inherent turbulent eddy fluctuations . The constant k is equal to 1/t 2 (=0.382) and is identified as the universal constant for deterministic chaos in fluid flows. The steady state emergence of fractal structures is therefore equal to
1/k = 2.62 (7)
Logarithmic wind profile relationship such as Equation 6 is a long-established (observational) feature of atmospheric flows in the boundary layer, the constant k, called the Von Karman 's constant has the value equal to 0.38 as determined from observations (Wallace and Hobbs , 1977 References ) .Equation 6 is basically an empirical law known as the universal logarithmic law of the wall ,first proposed in the early 1930s by pioneering aerodynamicists Theodor von Karman and Ludwig Prandtl, describes shear forces exerted by turbulent flows at boundaries such as wings or fan blades or the interior wall of a pipe. The law of the wall has been used for decades by engineers in the design of aircraft, pipelines and other structures (Cipra, 1996 References ).
In Equation 6, W represents the standard deviation of eddy fluctuations, since W is computed as the instantaneous r.m.s. (root mean square) eddy perturbation amplitude with reference to the earlier step of eddy growth. For two successive stages of eddy growth starting from primary perturbation w* , the ratio of the standard deviations Wn+1 and Wn is given from Equation 6 as (n+1)/n. Denoting by s the standard deviation of eddy fluctuations at the reference level (n=1) the standard deviations of eddy fluctuations for successive stages of eddy growth are given as integer multiple of s , i.e., s , 2s , 3s , etc. and correspond respectively to
statistical normalized standard deviation t = 0,1,2,3, etc. (8)
The conventional power spectrum plotted as the variance versus the frequency in log-log scale will now represent the eddy probability density on logarithmic scale versus the standard deviation of the eddy fluctuations on linear scale since the logarithm of the eddy wavelength represents the standard deviation i.e., the r.m.s. value of eddy fluctuations (Equation 6). The r.m.s. value of eddy fluctuations can be represented in terms of statistical normal distribution as follows. A normalized standard deviation t=0 corresponds to cumulative percentage probability density equal to 50 for the mean value of the distribution. Since the logarithm of the wavelength represents the r.m.s. value of eddy fluctuations the normalized standard deviation t is defined for the eddy energy as
![]()
![]()
![]() (9)
(9)
where L is the period in years and T50 is the period up to which the cumulative percentage contribution to total variance is equal to 50 and t = 0. LogT50 also represents the mean value for the r.m.s. eddy fluctuations and is consistent with the concept of the mean level represented by r.m.s. eddy fluctuations. Spectra of time series of meteorological parameters when plotted as cumulative percentage contribution to total variance versus t should follow the model predicted universal spectrum. The literature shows many examples of pressure, wind and temperature whose shapes display a remarkable degree of universality(Canavero and Einaudi,1987 References ).
The theoretical basis for formulation of the universal spectrum is based on the Central Limit Theorem in Statistics, namely, sample averages from almost any population encountered in practice tend to become normally distributed as the sample size increases. Therefore, when the spectra are plotted in the above fashion, they tend to closely (not exactly) follow cumulative normal distribution (see Section 6)
Though there is more information retained in the original spectra than conveyed in this form, universal spectrum for climate variability, if found to exist, will unambiguously rule out linear trends and predict changes in intensity of spectral components in response to changes (increase or decrease) in energy input into the atmospheric system.
(f) Mary Selvam (1993a References ) has shown that Equation 3 represents the universal algorithm for deterministic chaos in dynamical systems and is expressed in terms of the universal Feigenbaum's (Feigenbaum , 1980 References ) constants a and d as follows.
2a2 = p d (10)
where, p d ,the relative volume intermittency of occurrence contributes to the total variance 2a2 of fractal structures.
The Feigenbaum's constants a and d were originally computed numerically in the solutions of nonlinear equations(Feigenbaum 1980). Mary Selvam(1993a) arrived at Equation 10 relating a and d by visualizing round-off error growth mechanism to be similar to large eddy growth structures from intrinsic turbulence scale fluctuations. The model predicted (Mary Selvam 1993a) values of a and d (Equation 10) are not exactly equal to the numerically computed values (Feigenbaum 1980) and this difference was attributed(Mary Selvam 1993a) to intrinsic drawbacks in such numerical computations. However, the validity of this conclusion is yet to be tested. The round-off error growth mechanism given by Mary Selvam(1993a) may provide a physical basis for the observed sensitive dependence on initial conditions in dynamical systems, first identified by Lorenz(1963 References ) and later named deterministic chaos. Round-off error growth is inevitable in finite precision iterative computations and computer realizations of nonlinear dynamical systems will result in deterministic chaos even in the absence of errors such as grid-size related computation of continuum dynamical systems as discrete dynamical systems (Lorenz 1989 References ).
The Feigenbaum's constant a represents the steady state emergence of fractal structures. Therefore the total variance of fractal structures for either clockwise or anticlockwise rotation is equal to 2a2. It was shown at Equation 7 above that the steady state emergence of fractal structures in fluid flows is equal to 1/k( = t 2) and therefore the Feigenbaum's constant a is equal to
a = t 2 = 1/k = 2.62 (11)
(g) The relationship between Feigenbaum's constant a and statistical normal distribution for power spectra is derived in the following.
The steady state emergence of fractal structures is equal to the Feigenbaum's constant a (Equation 7 ). The relative variance of fractal structure for each length step growth is then equal to a2. The normalized variance 1/a2n will now represent the statistical normal probability density for the nth step growth according to model predicted quantumlike mechanics for fluid flows . Model predicted probability density values P are computed as
P = t - 4n (12)
or
P = t - 4t (13)
where t is the normalized standard deviation(Equation 8) and are in agreement with statistical normal distribution as shown in Table 1.
The periodicities T50 and T95 up to which the cumulative percentage contribution to total variances are respectively equal to 50 and 95 are computed from model concepts as follows.
The power spectrum, when plotted as normalized standard deviation t versus cumulative percentage contribution to total variance represents the statistical normal distribution(Equation 9),i.e, the variance represents the probability density. The normalized standard deviation values corresponding to cumulative percentage probability densities P equal to 50 and 95 respectively are equal to 0 and 2 from statistical normal distribution characteristics. Since t represents the eddy growth step n (Equation 8) the dominant periodicities T50 and T95 up to which the cumulative percentage contribution to total variance are respectively equal to 50 and 95 are obtained from Equation 5 for corresponding values of n , i.e.,0 and 2. In the present study of interannual variability, the primary perturbation time period Ts is equal to the annual (summer to winter) cycle of solar heating and T50 and T95 are obtained as
T50 = (2+t )t 0 @ 3.6 years (14)
T95 = (2+t )t 2 @ 9.5 years (15)
(h) The power spectra of fluctuations in fluid flows can now be quantified in terms of universal Feigenbaum's constant a as follows.
The normalized variance and therefore the statistical normal distribution is represented by (from Equation 13)
P = a - 2t (16)
where P is the probability density corresponding to normalized standard deviation t. The graph of P versus t will represent the power spectrum. The slope S of the power spectrum is equal to
![]()
The power spectrum therefore follows inverse power law form, the slope decreasing with increase in t. Increase in t corresponds to large eddies (low frequencies) and is consistent with observed decrease in slope at low frequencies in dynamical systems.
(I) The fractal dimension D can be expressed as a function of the universal Feigenbaum's constant a as follows.
The steady state emergence of fractal structures is equal to a for each length step growth (Equations 8 & 11) and therefore the fractal structure domain is equal to am at mth growth step starting from unit perturbation. Starting from unit perturbation, the fractal object occupies spatial (two dimensional) domain am associated with radial extent
t m since successive radii follow Fibonacci number series. The fractal dimension D is defined in Equation 1 as
![]()
where M is the mass contained within a distance R from a point in the fractal object. Considering growth from nth to (n+m)th step
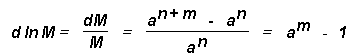 (18)
(18)
similarly
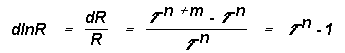 (19)
(19)
Therefore
 (20)
(20)
The fractal dimension increases with the number of growth steps. The dominant wavebands increase in length with successive growth step (Figure 6). The fractal dimension D indicates the number of periodicities incorporated. Larger fractal dimension indicates more number of periodicities and complex patterns.
j) The relationship between fine structure constant, i.e. the eddy energy ratio between successive dominant eddies and Feigenbaum's constant a is derived as follows.
2a2 = relative variance of fractal structure (both clockwise and anticlockwise rotation) for each growth step.
For one dominant large eddy (Figures 5 & 6) comprising of five growth steps each for clockwise and counterclockwise rotation, the total variance is equal to
2a2 x 10 = 137.07 (21)
For each complete cycle (comprising of five growth steps each) in simultaneous clockwise and counterclockwise rotations, the relative energy increase is equal to 137.07 and represents the fine structure constant for eddy energy structure.
Incidentally , the fine structure constant in atomic physics (Davies,1986;Gross,1985;Omnes,1994 References ) designated as a -1 ,a dimensionless number equal to 137.03604 is very close to that derived above for atmospheric eddy energy structure. This fundamental constant has attracted much attention and it is felt that quantum mechanics cannot be interpreted properly until such time as we can derive this physical constant from a more basic theory.
(k) The ratio of proton mass M to electron mass me , i.e. , M/me is another fundamental dimensionless number which also awaits derivation from a physically consistent theory. The value of M/me determined by observation is equal to about 2000. In the following it is shown that ratio of energy content of large to small eddies for specific length scale ratios is equivalent to M/me.
From Equation 21,
The energy ratio for two successive dominant eddy growth = (2a2 x10)2
Since each large eddy consists of five growth steps each for clockwise and anticlockwise rotation,
The relative energy content of primary circulation structure inside this large eddy
= (2a2 x 10)2/10
@
1879The cell dynamical system model concepts therefore enable physically consistent derivation of fundamental constants which define the basic structure of quantum systems.
These two fundamental constants could not be derived so far from a basic theory in traditional quantum mechanics for subatomic dynamics (Omnes, 1994 References ).