Arcs, chords & sagitta

Megalithic Yard Unearthed | home

Arcs, chords & sagitta

At times one may find a large Arc and want to know it's radius without having to physically measure it, or wish to lay out a large arc which has an extensive known radius, but which is impossible to demarcate because of terrain, rope stretch or some obstruction, then maybe the solution can be found from the following short cuts.

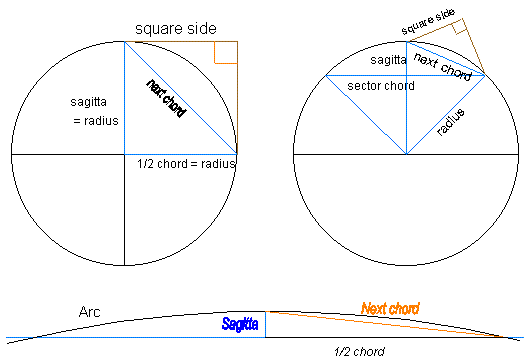
Here are some useful formulae. (see N.B. bottom of page)

Side of the Square = sqrt.Sagitta * sqrt.Radius. (The diagonal of this square is the Next Chord.)

Next Chord^2 = Side of Square * (2 * Side of Square)

Next Chord^2 / Sagitta = Diameter

Next Chord^2 = Sagitta^2 + 1/2 Chord^2

(Note the importance of finding the 'Next chord').

EXAMPLE 1:-

1. Draw a chord across the Circle, it doesn't have to be a large chord, quite a small one will do.

2. At the midpoint of the chord draw at right angles, a sagitta up to the arc.

3. Measure half the chord and the sagitta.

4. Add together the square of the sagitta and square of the half chord.

5. Dvide this sum by the sagitta.

6. The answer will be the DIAMETER of the circle.

Now you have the Radius, and half the chord divided by the Radius will be the SINE of half the angle of the Sector.

The length of the whole SECTOR ARC can now be determined by multiplying the whole sector angle in RADIANS by the RADIUS.

EXAMPLE 2:-

In this example the impractical large radius is known, the sagitta is decided upon, and the arc needs to be drawn. (Look at the right hand figure at top of page.) To do this without complicated arithmetic, it is beneficial to choose a radius whose square root is known, and a sagitta likewise.

1. Radius 484 (sqrt=22), Sagitta 25 (sqrt=5).

2. Square side = 22 * 5 = 110

3. Draw two sides of the Square at right angles and measure the diagonal (which I call 'Next chord') AC, with a piece of string. (Obviously the sq.side of 110 could be multiplied by sq.rt. 2 to obtain this diagonal, but I am assuming that Stone Agers could not do complicated maths!).

4. Lay out the Sagitta AB in the direction of the centre of the circle , and draw a chord Cc at right angles through B, of any suitable length. Now with the end of the diagonal string fixed at the start of the sagitta A, strike an arc to intersect this chord.at C.

5. This intersection will be a point on the arc. It is not necessary to know its exact distance from either end of the Sagitta.

6. Then by alternately superimposing the triangle and 'flipping' it, further arc points can be positioned.

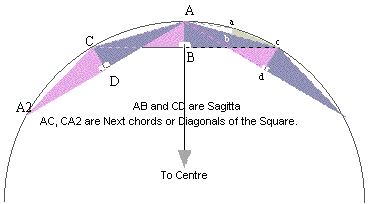
If you really must know the length of the Next Chord (diagonal), it is 155.563.. , the square of which is 24200. Dividing this by the Sagitta (25) gives a diameter of 968 (Radius 484).

24200 is also the side of the square multiplied by twice the side of the square (110 * 220)

Arc = Radius * Sector angle (in Radians)

1/2 chord / Radius = sine of half sector angle.

Chord length = Diameter * sine (180 / No. of divisions in circumference)

When ever a Circumference is divided into 30 arcs, the Diameter divided by the Sagitta on the chord of each arc will be

365.089777..

(i.e. The Sagittae on each Lintel Arc is 1/365.08..th.. of the Sarsen diameter.).

N.B.

The first set of formulae at the top of the page were happened upon whilst looking at Thoms interpretation of Avebury. in particular the 750 MY radius for the two shallow arcs. I was trying to see if it were possible to mark out arcs without knowledge of Pi or Pythagoras, and indeed it is possible, but one must know about "squares".and "square roots". I had the idea that the sagitta of one of the arcs might be 1/100th of the radius, which would have given a Square Side of 75 MY and an Hypotenuse of the square (my Next Chord) of 106.066+ ft. (75 sqrt2) This measure is also to be found as the SS of the Ditch circle at Stonehenge. Fig 4. Stonehenge.

updated Feb 2005 and June 2005

Previous Page Home Page Back to Top Next Page