(draft)
 

Abstract : An algorithm well suited for implementation on a FPGA is developed. The algorithm distributes computation and memory requirements evenly among the processors. The algorithm integrates the ram used on to the procesor itself to achieve higher speed. It also reduces the width of the interconnections between the different stages of FFT.
 

INTRODUCTION

Parallel pipelined FFT processors are employed to meet the growing demand of high processing rate. Highly parallel implementations obtain high computation rates but requires the simultanious distribution of all data samples. The high rate of distribution of data required to keep the processors busy is impossible to achive especially in real time applications involving word-serial data. This problem coupled with limited i/o resources in FPGAs makes the parallel algorithm inefficient.

The cascade FFT computes one transform in O(N) processing cycles, producing the o/p sequentially at the input data rate. So the cascade FFT is ideally suited for 1-dimensional real-time signal processing where data arrival is word-serial in nature. But cascade FFT requires registers organised as shift-registers between butterfly computation units with varying depths from 2 to N/2 words. Jones and Sorenson proposed an algorithm for overcoming this, in evaluating their multiprocessor architecture for FFT. Yu Tai Ma proposed an algorithm to reduce the number of twiddle factors in each processor to a minimum. These ideas with some modifications are used to design a 32-point FFT processor using multiple FPGAs.
 

A PARALLEL FFT ALGORITHM

The DFT of N-point is defined as

X_k = _m=0^n-1 x_m. _nw^mk -------------------------------------------------------(1)

w_n^mk = exp(-j.2/N m.k)

k = 0,1,.......,N-1

N = 2ⁿ

N = N₁.N₂

m = N₁m₂ + m₁

k = N₂k₁ + k₂

N₁ = 2ⁿ¹

N₂ = 2ⁿ²

m₁,k₁ = 0,1,2,3,...........,N₁-1

m₂,k₂ = 0,1,2,3,...........,N₂-1

Then eq.(1) can be expressed as

X_{N2k1 + k2} = _m1=0^N1-1 ( _N1N2 W^{m1(N2k1 + k2)} ) _m2=0^N2-1 (x _{N1m2 + m1} . _N2W^m2k2 ) --------(2)

eq.(2) can be further expressed as

Y_{N1k2 + m1} = _m2=0^N2-1 (x _{N1m2 + m1} . _N2W^m2k2 )

X_{N2k1 + k2} = _m1=0^N1-1 Y_{N1k2 + m1} . ( _N1N2 W^{m1(N2k1 + k2)} ) -------------------------(3)

eq.(3) can be computed easily through the FFT algorithm and (4) can be computed in a similar way as is the standard FFT algorithm. The flow for a 16-point FFT using such an algorithm is as shown in fig.(1).

Fig.1. Flow diagram for 16-point FFT
 

Fig.2 : Division of computations among the FPGAs
 
 
 
 
 
 
 
 
 

The division of computations among the FPGAs is as shown in fig.2. There are 4 independent length-4 transforms in the first 2 stages of the radix-2 decimation in time algorithm as the first part of FFT computation. The last 2 stages of 4 independent length-4 transforms form the second part.There are 4 processors at each pipeline stage and each FFT processor computes a 4 point FFT. The reduced twiddle factor tables stored are shown in table-I
 
 
 

Table 1 : REDUCED TWIDDLE FACTOR TABLES STORED IN FFT PROCESSORs at second pipeline stage.

PROCESSOR NO.	0	1	2	3
0   1   2   3	--   --   --   --	16W0   16W1   16W2   16W3	16W0   16W2   16W4   16W6	16W4   16W5   16W6   16W7

 
 
 

Processors

The processors used in the two pipeline stages incorporate both the twiddle factor ROM and the data RAM on the chip. The look-up table based logic in some of the commercial FPGAs makes this idea all the more efficient. Each processor is structured internally as shown in Fig.3. The single input and output buses in each processor is time shared between the different butterfly computation units for i/o of the samples and transforms.

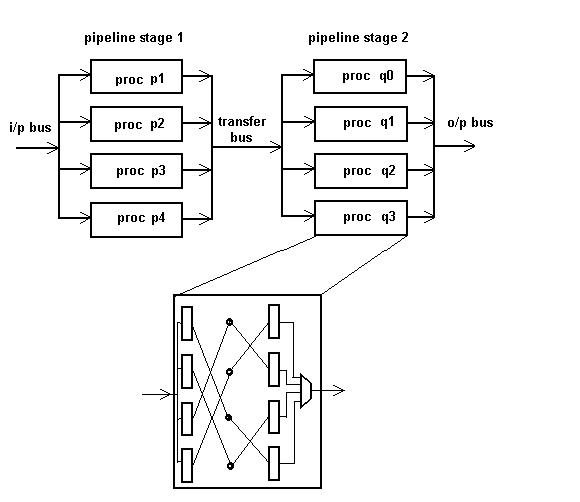
Fig.3: Processor organisation and internal structure of FFT processors.
 
 
 
 
 

There is a single input[x(m)], output[X(k)] and transfer[Y(N₁k₂+m₁)] bus time-shared between the processors. To prevent contention of the bus, data transforms are done as in Fig.4.

output bus tranfer bus      input bus

X1 from q2  y4 from p0  to q2  x0 to p0

X9 from q2  y5 from p1  to q2  x1 to p1

X5 from q2  y6 from p2  to q2  x2 to p2

X13 from q2  y7 from p3  to q2  x3 to p3

 

output bus tranfer bus        input bus

X3 from q3  y12 from p0  to q3  x4 to p0

X11 from q3  y13 from p1  to q3  x5 to p1

X7 from q3  y14 from p2  to q3  x6 to p2

X15 from q3  y15 from p3  to q3  x7 to p3

 

output bus tranfer bus        input bus

X0 from q0  y0 from p0   to q0  x8 to p0

X8 from q0  y1 from p1  to q0  x9 to p1

X4 from q0  y2 from p2  to q0  x10 to p2

X12 from q0  y3 from p3  to q0  x11 to p3

 

output bus tranfer bus        input bus

X2 from q1  y8 from p0   to q1  x12 to p0

X10 from q1  y9 from p1  to q1  x13 to p1

X6 from q1  y10 from p2  to q1  x14 to p2

X14 from q1  y11 from p3  to q1  x15 to p3

Fig. 4 : Synchronisation of data transfers for time sharing the buses.

A controller generating control signals for data transfers is used for write enables to input registers and for the mux select signals at the output of each processors. To reduce the number of control signal lines to be generated by the controller all the three tranfers, namely input, output and intermediate transefers are done with the same signals.

(incomplete)