- Analogy serves to help one systematically study a new field
by using a familiar model as the guide. Indeed, analogy allows us
to predict and formulate the corresponding theorems in the new field although
their proofs can be a quite different matter.
Remark. If we consider the Gâteaux variation of a functional defined in an open subset Y of a normed linear space [Sag, p.26, Definition 1.5], then the calculus of variations on Y [Sag, p.38, Theorem 1.8.2] includes both "the calculus of variation on a space of functions [Sag, p.34, l.-13-l.-1; p.37, l.9-l.-1; p.38, l.-7-l.-3]" and "the theory of extreme values in differential calculus [Sag, p.42, l.11]" as its special cases.Differential Calculus Calculus of variations Functions of n variables Functions of infinitely many variables (method of finite differences [Fomi, p.4, l.- 17, l.- 10]) Variation of a function 1. Variation of a functional defined on a fixed region [Fomi, p.153, (4)]. 2. Variation of a functional defined on a variable region [Fomi, p.173, (95)].
All the partial derivatives of a function vanish at an extremum. The variational derivative of a functional vanishes at every point (Euler’s equation) [Fomi, p. 28, l.- 12-l.- 4] Formulas for differentiating sums and products of functions, composite functions, etc. Analogs are valid [Fomi, p.29, l.11-l.13] Method of Lagrange multipliers for finding extrema of functions of several variables. 1. The isoperimetric problem [Fomi, p.43, Theorem 1]. 2. Finite subsidiary condition: a limiting case of an isoperimetric problem [Fomi, p.48, l.- 8].
A quadratic form is positive definite Û its principal minors are all positive [Fomi, p.127, l.10]. [Fomi, p.117, Theorem 3; pp.125-129, § 30]. Necessary conditions for a minimum [Fomi, p.97, l.- 4]. Weak minimum : 1. Euler's equation [Fomi, p.15, Theorem 1]. 2. Legendre's condition [Fomi, p.119, Theorem 1] or [Akh, p.68, Theorem 2]. 3. Jacobi's condition [Fomi, p.124, Theorem 5]. Strong minimum: Weierstrass’ condition [Akh, p.65, Theorem 1].
Sufficient conditions for a minimum [Fomi, l.- 6-l.- 5]. Sufficient conditions for a weak (strong) minimum [Fomi, p.116, Theorem; p.125, Theorem 6] ([Fomi, p.148, Theorem1]).
- The correct attitude toward the use of analogy.
When we study a new field, analogy can be used in the beginning stage of investigation. However, analogy should not be used in the final stage for conclusion. Suppose we ask why the actual motion should be characterized by stationary action rather than least action. [Fomi, pp.159-162, §36.2] gives a sophisticated explanation with a correct attitude. In contrast, [Hec, p.111, Fig. 4.37(c)]considers only three simple cases with an incorrect approach. Hecht's oversimplification of the complicated problem and the mistakes involved in his argument [Hecht mistakes an admissible curve for a point] are due to his misuse of the analogy between the calculus of variations and differential calculus.
- How to exploit the analogy.
Example 1. If we replace i in [Guo, p.368, (1)] by -i, we obtain [Guo, p.368, (2)]. Similarly, if we replace i in [Guo, p.372, (14)] by -i, we obtain [Guo. p.372, (15)]. We would like to apply this analogy in detail to the proof of [Guo, p.372, (14)] in order to derive [Guo, p.372, (15)]. That is, we want to replace i by -i in each step of the proof. Using [Guo, p.370, (7); p.358, (16)], we can express Hu(2) as c{I1+I2+I3+I4} , where I1, I2, I3, I4 are similar to the corresponding integrals in the bracket in [Guo, p.371, l.-3-l.-2]. Now there is a problem. The exponents in I1 and I2 have a factor i rather -i, so we must change the variable q into -q1. After we perform this trick, we can replace i by -i step by step in the proof of [Guo, p.372, (14)] to derive [Guo, p.372, (15)].
Example 2. In order to prove [Guo, p.373, (17)], all we need to do is to replace i by -i in each step of the proof of [Guo, p.373, (16)] except we have to perform the following trick first: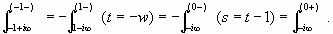
Remark. The i in [Guo, p.373, l.12] should not be replaced by -i because that i goes with formula [Guo, p.305, (3)]. If we were to change i to -i in that formula, the formula would become incorrect.
- If two theorems are similar, we must prove their similarity rather than just
mention it.
The proof of [Zyg, vol.1, p.3, (2.1)] is quite different from that of [Edw1, p.517, (3)], but Zygmund says that [Zyg, vol.1, p.3, (2.1)] corresponds to integration by parts in the theory of integration [Zyg, vol.1, p.3, l.-4-l.-3]. We cannot use [Edw1, p.517, (3)] to prove [Zyg, vol.1, p.3, (2.1)] because a step function is not differentiable at certain points. Therefore, we must use [Zyg, vol.1, p.3, (2.1)] to prove [Edw1, p.517, (3)].
Proof. Let x0, …, xm be a partition of [a, b]. By [Zyg, vol.1, p.3, (2.1)],
Sk=0m f(xk)g(xk) = Sk=0m-1[f(x0)+……+f(xk)](g(xk)-g(xk+1))+[f(x0)+…+f(xm)]g(xm).
Multiply both sides by (b-a)/n, and then let m ® +¥.
- Prove the statements given in [Wat1, p.348, l.14].
Proof. a + b = 2n+1/2 G(1+n/2)/G((1-n)/2) (1).
a - b = - i 2n+1/2 G((1+n)/2)/G(-n/2) (2).
2a = (-1)n2-1/2p-3/2G(n+1)p([sin (-np/2)]-1- i[cos (-np/2)]-1) [(1)+(2)]/2.
2b = (-1)n2-1/2p-3/2G(n+1)p([sin (-np/2)]-1+ i[cos (-np/2)]-1) [(1)-(2)]/2.
It would be difficult to solve b if one tries to substitute the value of a into (1). - If A and B are similar, we should manage to make B play the same role as
A in order
to avoid repetition or complication.
Example 1. [Bir, p.271, l.-16-l.-14] - (Comparing the degree of similarity) We have two options in proving [Wat, p. 79, (1)(ii)]: Use [Wat, p.78, (6); p.79,(1)(i)] or use [Wat, p.78, (8); p.74, (3)(i)]. Since [Wat, p.73, (2)(i)] and [Wat, p.78, (6)]{Watson66} are similar, Kn is more closely to Hn than to In. Consequently, the latter option is the better choice.¬
- Links {1,
2}.
Example 2. For the proof of the oscillation theorem given in [Inc1, p.237, l.4-l.14], Ince suggests that we let |l| be our new l, and then apply [Inc1, p.235, Theorem III] to the two cases given in [Inc1, p.236, l.2-l.3]. However, if we make the variable transformation l® -l, the second case will become the first case.