- The following selections are masterpieces in
differential equations
from a variety of sources. They are related to geometry or physics in some way.
Some of them are difficult to read. However, it is rewarding if you understand
them eventually.
- Cusp and envelope [Inc, §24-§27].
- Green's function [Bir, p.48, Example 6; p.53, Example 8].
- Method of Liapunov [Bir, chap.5, §9].
- Sturm's theorems on the Zeros of Solutions of Second-order Equations [Arn1, §27.7].
- Differential calculus.
- Preliminaries.
- The vector product
Remark 1. Modern textbooks often ignore the definiteness of the vector product. [Wea1, p.3, l.18-p.4, l.13] provides a careful treatment.
Remark 2. The concept of moment originates from physics. Without the help of physical terms and a picture [Kara, p.7, Fig. 1.6], it is difficult to understand the abstract definition given in [Wea1, p.5, l.5-l.7]. - The Taylor series expansion
- f(r+h) = f(r)+(h×Ñ) f(r)+(2!)-1(h×Ñ)2 f(r)+…+(n!)-1(h×Ñ)n f(r)+…. [Chou, p.302, l.4].
- Taylor's formula with integral remainder [Tay, p.112, Theorem II].
- Differentiating integrals
- (Finite integrals
with respect to real t, real z): [Wid, p.350, Theorem 8]
® [Wid, p.352, Theorem 10] ®
[Sak, p.45, Theorem 1.5].
Remark. [Wid, p.353, Theorem 11; Example B] are corollaries of the above theorems. - (Infinite integrals with respect to real t, real z): [Wat1, §4.44, p.73, (I); p.74, Corollary].
- (Finite integrals with respect to real t, complex z): [Wat1, p.92, §5.31]. The proof of the complex case [Wat1, p.92, l.13-l.19] is the same as the proof of the real case [Wid, p.352, Theorem 10].
- (Infinite integrals with respect to real t, complex z): The case of infinite integrals [Gon, pp.526-527, Theorem 8.4] is derived from the case of finite integrals [Wat1, p.92, l.13-l.19] by means of [Ru2, p.230, Theorem 10.28]. By using [Ru2, p.27, Theorem 1.34], the statement given in [Gon, pp.526-527, Theorem 8.4] allows González to eliminate the superfluous hypotheses of the theorem given in [Wat1, p.92, §5.32]. The proof of [Gon, pp.526-527, Theorem 8.4] is simpler than both the proof of [Lang1, p.270, Lemma] and the proof of [Wat1, p.74, Corollary]. See also [Ru2, pp.246-247, Exercise 16].
- (Integrals on arcs in a complex plane, complex z): [Ahl, p.121, Lemma 3].
- (Using a limiting procedure when the integrand is singular): [Jack, p.35, l.2-l.10].
- (Finite integrals
with respect to real t, real z): [Wid, p.350, Theorem 8]
® [Wid, p.352, Theorem 10] ®
[Sak, p.45, Theorem 1.5].
- The inverse function theorem [Spi1, p.35, Theorem.
2-11 [1]; functions in implicit form: Cou2, vol.
2, p263, l.-16-l.-8]; local linearlization of
differentiable mappings [Spi, vol.1, p.56, Theorem 9; p.59, Theorem 10]; the
implicit function theorem [Wid, p.56, Theorem 14; p.59, Theorem 16].
Remark 1. One may understand the essence of the implicit function theorem more easily from the proofs of [Wid, p.56, Theorem 14; p.59, Theorem 16]. These two theorems are clear and useful versions of the implicit function theorem. Other versions are either too general to highlight the key point, too abstract to help readers visualize the picture, or too complicated to apply to practical problems.
Remark 2. The proof of [Kli, p.6, Theorem 0.5.2] follows the model given in [Kli, p.6, l.11-l.20]. However. in the proof of [Kli, p.6, Theorem 0.5.2], Klingenberg uses many identification maps, but fails to define them explicitly. The proofs given in [Spi, vol.1, p.56, Theorem 9; p.59, Theorem 10] are clearer and more accessible.
Remark 3. Before stating the implicit function theorem, Courant provides stimulating examples to explain why he formulates the theorem as he does [Cou2, vol. II, pp.219-221, §3.1.b]. After stating the implicit function theorem, Courant shows us how we use this theorem to solve practical problems [Cou2, vol. 2, pp.221-225, §3.1.c]. Motivation and application are integral parts of understanding a mathematical theorem, but are often neglected in our learning process.
Remark 4. The key point of the inverse function [Cou2, vol. 2, p.262, l.2-l.5] is to solve x [x=X(u,y)] using the equation [Cou2, vol. 2, p.261, (33a)(i)], and then solve y using the equation obtained by substituting the expression x=X(u,y) into [Cou2, vol. 2, p.261, (33a)(ii)]. The purpose of mathematics is to teach students to observe, to think, and to solve problems, not to engage in insignificant generalization of theorems.
Remark 5. To prove the theorem of the decomposition into primitive mappings, Courant does nothing but make an insightful side comment [Cou2, vol. 2, p.264, l.-14-l.-9] on his proof of the inverse function theorem. In contrast, Rudin builds complicated machinery to prove this decomposition theorem as a theorem separate from the inverse function theorem [Ru1, p.199, l.-9-p.201, l.6]. In my opinion, c(x,h) in [Cou2, vol. 2, p.264, (34q)] is more easily visualized than gm-1(y) in [Ru1, p.200, (51)]. The purpose of mathematics is to help students understand a theorem's insight rather than bury it in complicated but insignificant structures.
Remark 6. The inverse function theorem is essentially a topological theorem. See [Mun00, p.383, Theorem 62.3].
Remark 7. [Gon, p.543, Theorem 8.11] provides the most effective method of finding inverse functions [1]. - Area of a curved surface (in the form of z = f(x,y) [Cou1, vol. 2, p.424, (29a); in the parametric form [Cou2, vol. 2, p.428, (30c)]).
- Solid angles: [Wangs, p.58, (4-3); Fig. 4-1; Fig. 4-2].
- Normal derivatives: ¶f/¶n = fx(¶y/¶s) - fy(¶x/¶s) [Cou1, vol. 2, p.270, l.3].
- Orientation of curves
- Curves in parametric form C(t) = (x(t), y(t)) [Cou2, vol. 1, p.339, l.16-p.346, l.-1].
- Curves in implicit form F(x,y)=0 [Cou2, vol. 2, pp.230-235, §3.2.a].
- Curvature
(1). Definition [Cou2, vol. I, p.354, (14)].
(2). Curves in parametric form C(t) = (x(t), y(t)) [Cou2, vol. 1, p.355, (15)].
(3). Curves represented by functions y = f(x) [Cou2, vol. 1, p.357,(16)].
(4). Curves in implicit form F(x,y)=0 [Cou2, vol. 2, p.232, (14a)]. - How we determine the sign of curvature
(1). Curves in parametric form C(t) = (x(t), y(t)) [Cou2, vol. 1, p.355, l.18-p.358, l.14].
(2). Curves in implicit form F(x,y) = 0
(a). The curve is given by F(x,y) = 0. (b). The normal [Cou2, vol. 2, p.231, (12c)] points to the region F > 0, so the normal determines the region F > 0. (c). If the tangent to the curve near the point of contact lies in the region F ³ 0, then the curvature k is positive [Cou2, vol. 2, p.232, l.-3-l.-1]. - (1). The oriented area within a simple closed oriented curve [Cou2, vol.
1, p.365, (20)].
Application in thermal physics [Cou2, vol. 1, p.419, l.19-l.18]. Example
[Hua, p.11, Fig. 1.4].
(2). Areas bounded by closed curves [Cou2, vol. 1, pp. 430-435, §A.2].
- (Orientation of
surfaces) [1]
- Nonorientable surfaces [Cou2, vol.2, p.582, l.3-p.583, l.-13].
- Orientable surfaces.
Orientation of an ordered basis [Cou2, vol.2, p.196, (82b)] ® orientation of an ordered set of independent vectors [Cou2, vol.2, p.200, l.5] (the positive orientation agrees with the usual sense of counterclockwise rotation when we view the ordered set from the positive side of an oriented plane [Cou2, vol.2, p.200, l.-13-p.201, l.19]) ® A surface oriented positively with respect to the coordinate axes [Cou2, vol.2, p.578, l .-5] (a region [Cou2, vol.2, p.580, l .10; a simple surface: p.634, l.-12] or a coordinate patch with parameters u, v [Cou2, vol.2, pp.580-581, (40n, o, p, s)]) ® orientable surfaces ([O'N, p.178, Theorem 7.5]; methods of realization [Cou2, vol.2, p.585, (41a) & p.586, (41e); elementary surfaces in the n-dim Euclidean space: p.646, l.21]).
- The vector product
- Gauss' theorem [Cou1, vol.2, pp.359-365].
Versions: Cartesian coordinates [Cou1, vol.2, p.364, l.13], the vector form [Cou1, vol.2, p.364, l.17] and the differential form [Cou2, vol.2, p.545, (2a)] (the differential form allows us to use diffeomorphisms [Arn1, p.61, l.-6] to select a coordinate system that is convenient for calculating the contour integral [Cou2, vol.2, p.550, l.-1]) .
Remark 1. In the 2-dim case, both the divergence theorem and Stokes' theorem reduce to Gauss' theorem [Cou1, vol.2, p.364, l.17; p.365, l.-14].
Remark 2. Written in their differential forms, the divergence theorem and Stokes' theorem are similar in the 3-dim case (Compare [Cou2, vol.2, p.601, (53) with [Cou2, vol.2, p.612, (74)]). - Green's theorems [Cou2, vol.2, p.557, l.7 & p.558, (15)].
- The divergence theorem [Cou1,
vol.2, pp.385-387].
Versions: Cartesian coordinates [Cou1, vol.2, p.386, l.10] (good for tensor analysis [Lan7, p.5, (2.2)]), the vector form [Cou1, vol.2, p.387, l.-11] (good for geometric interpretation).
Remark 1. The proof given in [Wangs, pp.21-24, §1-14] features an unambiguous definition [Wangs, p.17, l.-8-l.-4] of the vector element of area on a closed surface. [Wangs] uses the divergence theorem to prove [Wangs, p.24, (1-66); p.35, (1-122) & (1-123)].
Remark 2. The proof of the divergence theorem given in [Fan, §2.6] is better than that given in [Wangs, §1-14] because the former proof highlights the key geometric idea and is independent of coordinate systems. - Stokes'
theorem [Cou1, vol.2, pp.392-396].
Remark 1. The idea of its proof is based on the plane version of Gauss' theorem (A curved surface can be approximated by inscribed polyhedrons (Warning [Cou2, vol.2, p.421, l.-10-p.422, l.16]) or transformed by a coordinate patch [Cou2, vol.2, p.612, l.-6-p.613, l.12].)
Remark 2. The proof given in [Wangs, pp.24-26, §1-15] features an unambiguous definition [Wangs, p.17, l.17-l.23] of the vector element of area on an open surface. [Wangs] uses Strokes' theorem to prove [Wangs, p.27, (1-73); p.35, (1-124)].
Remark 3. In general, the geometric interpretation in [Kara, Chap. 4] is clearer and more organized than that in [Fan, chap. 2]. However, the definition given in [Fan, p.64, (2.101)] is simple and natural, while the definition given in [Kara, p.68, (4.19)] is artificial. Furthermore, the proof of [Kara, (4.19) Þ (4.25)] is much more complicated than the proof of [Fan, (2.101) Þ (2.126)]. Consequently, Fano's approach makes it easier to deal with curl. - Generalization of a, b, c and d: [Spi1, p.124, l.-7-p.125, l.-3].
- Gauss' theorem [Cou1, vol.2, pp.359-365].
- The integral solution of the Poisson equation [Kara, p.100, (5.75); Chou, p.31, l.-3-p.32,
l.9].
Remark. Jackson makes a serious mistake in [Jack, p.35, l.-11] because he tampers with the given assumption. The value of Ñr is given and Jackson does not have the authority to make it equal to 0. The R that Jackson chooses in [Jack, p.35, l.-17] can make r small, but cannot affect the given value of Ñr. - E = -ÑF Û Ñ´E = 0
in a simply connected domain.
Proof. Þ: Ñ´Ñu = 0 [Wangs, p.15, (1-48)].
Ü: Let F (x) = òC E1dx1+E2dx2+E3dx3, where C begins at a fixed point x0 and ends at x. By Stokes' theorem, is independent of the contour of integration. - B = Ñ´A
Û Ñ×B = 0.
Proof. Þ: Ñ× (Ñ´A)=0 [Wangs, p.15, (1-49)].
Ü: Read http://www.math.unl.edu/~mbrittenham2/classwk/208s04/inclass/divergence-frees_are_curls.pdf - The Helmholtz theorem [Case 1.
F(r) = O(r-2): Chou, pp.583-586;
case 2. F(r)®0 as |r|®¥: read http://farside.ph.utexas.edu/teaching/em/lectures/node37.html]
- Its physical meaning is given by [Wangs, pp.37-38, §1-20].
- Other related comments [Kara, pp.94-95, §5.9].
- E = -ÑF Û Ñ´E = 0
in a simply connected domain.
- Formulas.
-
Laplacian.
- spherical coordinates (various proofs: 1. direct substitution using [Lev2, p.107, (5.62)-(5.64)]. 2. invariant character of the Euler equations [Cou, vol.1, p.225, (63)]. 3. The divergence theorem [Cou2, vol.2, p.610, (69)].)
- Two remarks on [Wangs, p.34, (1-121)]
- The complex expression of mechanical operations in [Wangs, p.34, (1-121)]
impedes intuitive understanding.
(A·Ñ) B = (Ax ¶/¶x + Ay ¶/¶y + Az ¶/¶z) (Bx, By, Bz)
= ((Ax¶/¶x + Ay¶/¶y + Az¶/¶z)Bx, (Ax¶/¶x + Ay¶/¶y + Az¶/¶z)By, (Ax¶/¶x + Ay¶/¶y + Az¶/¶z)Bz) (the operator applies to each component). This interpretation can be summarized in a shorter form: [(A·Ñ) B]i = A·(ÑBi). - If B = f v, where v is a constant vector, then (A·Ñ)(f v) = [A·Ñf ]v. This statement is equivalent to (i).
- The complex expression of mechanical operations in [Wangs, p.34, (1-121)]
impedes intuitive understanding.
Remark 2. For cylindrical coordinates, we use row two of [Wangs, p.29, (1-76)] to express Ñ×A [Wangs, p. 31, (1-87)] and use row three of [Wangs, p.29, (1-76)] to express Ñ´A [Wangs, p.31, (1-88)]. We use the same idea to express Ñ×A and Ñ´A for Cartesian coordinates and spherical coordinates. Thus, we recognize a pattern that only through geometric considerations can we find the most effective method to prove [Wangs, p.31, (1-87) & (1-88)]. -
Laplacian.
- Preliminaries.
- Calculus of variations
- Fermat's principle (the principle of least action) is a mathematical
theorem [Fomi, p.84,
Theorem].
Remark 1. The proof of [Fomi, p.84, Theorem] shows that Fermat's principle is nothing but the equation of motion disguised in an artificial form. Consequently, the discussion given in [Fur, p.14, l.12-l.13] merely reveals Furtak's ignorance. Philosophy serves to clarify a picture through a thorough study rather than mystify the picture.
Remark 2. (Stationary points) The case of the global minimum and that of a local minimum in a discussion of Fermat's principle are not distinguishable unless the discussion includes both [Hec, p.106, Fig. 4.28] and [Born, p.130, Fig. 3.12]. The case of local maximum and that of local minimum in a discussion of Fermat's principle are not distinguishable unless the discussion includes [Hec, p.110, r.c., l.11-l.28]. Only after we distinguish among the above cases are we able to find all possible cases for stationary points. Only after we study [Born, p.730, (58); p.731, (60)] are we able to clarify the relationship between Fermat's principle [Born, p.128, l.-16-l.-12] and the weaker form of Fermat's principle [Born, p.129, l.1]. - The modern formulation of Fermat's principle [Hec, p.109]:
y is an extremal of the functional J[y]
Þ the variational derivative of J[y] vanishes [Fomi, p.28, l.-10; p.35, Theorem]. - For physical applications, it is convenient to reduce the variational derivative to the ordinary derivative by using the
linking device
dy = eh(x) [Cou, vol. 1, p.184, l.20].
Remark. Due to the absence of the above crucial link between the variational derivative and the ordinary derivative, the application given in [Fur, p.11, l.13] fails to closely connect to its rigorous theoretical ground and the theoretical formula given in [Fomi, p.29, l.-10] fails to appear in a form ready for useful applications. - The proof of [Fomi, p.15, Theorem 1] breaks the elegance of the proof given in [Cou, vol. 1, chap IV, §3.1] into pieces and makes the essence of the proof unrecognizable.
- [Born, Appendix I], [Fomi] and [Sag]
- The strong minimum in [Born, p.730, l.12]. the weak minimum in [Born, p.731, l.8]. and the minimum in [Fomi, p.12, l.-5-p.13, l.1; §24, Theorem 1 & Theorem 2] all refer to a local minimum. In calculus of variations, we are not interested in the global minimum. The precise definitions of a strong extremum and a weak extremum are given by [Fomi, p.13, l.4-l.12].
- We can use [Born, p.719, (2)] and [Fomi, p.9, Lemma 1] to prove [Born, p.720, (7a) & (7b)].
- The statement given in [Born, p.135, footnote *] is proved in [Fomi, p.72, (16)].
- [Born, Appendix I, §§2-3], [Fomi, §33] and [Sag, §3.2; p.141, (3.3.2)] all discuss Hilbert's invariant integral. The discussion given in [Born, Appendix I, §§2-3] is the most elegant. The field given in [Born, Appendix I, §3] refers to the field defining y' = v [Arn1, p.28, l.9-l.-10] to which Euler's equations can be reduced. The definition of fields given in [Fomi, p.132, Definition 1 & Definition 2] is too complicated.
- "Let P1Q be any extremal" in [Born, p.731, l.-8] should have been "Let P1Q be any curve".
- Fermat's principle (the principle of least action) is a mathematical
theorem [Fomi, p.84,
Theorem].
- Sturm-Liouville Systems [Bir, chap. 10 & chap. 11].
- Regular systems:
Eigenfunctions that have different eigenvalues are orthogonal.
- separated endpoint conditions [Bir, p.258, Theorem 1].
- periodic endpoint conditions [Bir, p.259, Corollary].
- Singular systems: Square-integrable eigenfunctions
u and v
that belong to different eigenvalues are orthogonal [Bir, p.264, Theorem
2] if u and v satisfy the boundary condition of [Bir, 264, (12)].
Remark. In [Bir, chap. 10, §4, Example 5, Example 6 and Example 7], Birkhoff only shows that certain values are eigenvalues. Expanding on this idea, [Cou, vol.1, chap. V, §10] explains why other values cannot be eigenvalues. - Sturm Comparison Theorem [Bir, p.268, Theorem 3].
- The sequence of eigenfunctions [Bir, p.273, Theorem 5].
- The continuous spectrum [Bir, p.291, Theorem 13; p.292, Corollary 2].
- The discrete spectrum [Bir, p,292, Theorem 14].
- Completeness of eigenfunctions [Bir, p.313, Theorem 11].
- [Lan3, p.60,
l.-7-l.-4, the oscillation theorem] can be easily derived from
[Bir, p.268, Theorem 3 or p.273, Theorem 5] (Although these two
theorems require that [a,b] be a finite interval, their
proofs are still valid if the endpoints of the interval are
±¥). However, using a general theorem to
prove a statement often blurs the essence of the statement.
The following more direct proof clearly reveals the essence of
the oscillation theorem.
Proof.
Let a and b are consecutive zeros of yn. Say y'n(a)>0 and y'n(b)<0.
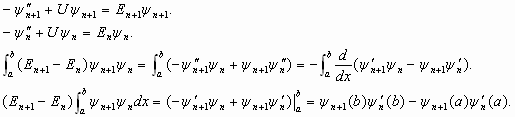
If yn+1>0 in (a,b), then RHS<0, but LHS>0.
If yn+1<0 in (a,b), then RHS>0, but LHS<0.
Hence yn+1 change sign in (a,b).
- Regular systems:
Eigenfunctions that have different eigenvalues are orthogonal.
- To view a concept from a single perspective is often not enough. To gain a complete picture, we must
view the concept from a complementary perspective.
Example (Conjugate points). [Fomi, p.106, Definition] and [Bir, p.52, l.17-l.28].
Green's functions.
- The physical origin: [Arf, p.511, l.8].
- The general definition of Green's function ([Arf, p.512, (8.159) ® [Mor, part 1, p.884, (7.5.37)] ® [Ru3, p.192, l.-5]).
- (Main usage) Expressing the solution of a nonhomogeneous self-adjoint differential equation in terms of Green's function [Arf, p.514, l.-11-l.-6].
- (Existence) [Ru3, p.195, Theorem 8.5].
- (Symmetry [Jack, p.40, l.9-l.12])
Proof. Let G0(r)= (4pr)-1, where r = |x-x0|-1.
f(x) = lim d®0 ò |x-x0| = d f (y)(¶G0/¶n) dy.
Let u(x) = G(a,x), v(x) = G(b,x), and W' = W - {x: |x-a| = e or |x-b| = e }.
0 = ò W' (uÑ2v-vÑ2u) dx
= ò ¶W (u(¶v/¶n-v(¶u/¶n)dx +Ae+Be,
where Ae = - ò |x-a| = e (uÑ2v-vÑ2u) dx and Be = - ò |x-b| = e (uÑ2v-vÑ2u) dx.
lim e®0 Ae = ò |x-a| = e (G0(|x-a|) + H(x))(¶v/¶n)-v(¶(G0(|x-a|) + H(x))/¶n)dx = -v(a)
because the contributions from harmonic H are 0. Similarly, lim e®0 Be = u(b).
Since ò |x-a| = e G0(|x-a|)(¶v/¶n)dx®0 as e®0, v(a) = u(b). - (Forms) Expressing Green's function in terms of
- a complete set of eigenfunctions [Mor, part 1, p.884, (7.5.39); the Fourier transform: Arf, (8.213) & (8.218)].
- distributions [Ru3, p.378, l.-6].
- (Effective methods of finding the Green function for a boundary-value problem):
- The method of images (for planes and spheres) [Wangs, §11-2].
- The Green function expansion in spherical coordinates using the basis of spherical harmonics (for shells) [Jack, §3.9].
- The Green function expansion in cylindrical coordinates using the basis of modified Bessel functions [Jack, p.126, (3.145) & (3.149)].
- The Green function expansion using the basis of eigenfunctions [Jack, p.128, (3.160)].
- (Addition theorem for spherical harmonics)
[Jack, pp.110-111, §3.6], [Coh, pp.688-689] and [Mer, pp.250-251] all prove the addition theorem for spherical harmonics. Among the three proofs, Jackson's is the most concise and Cohen-Tannoudji's is the easiest to understand. Merzbacher's is unnecessarily complicated. The simplicity of Jackson's proof is due to the use of [Jack, p.109, (3.59)]. The key idea behind this simplification is to eliminate the terms containing m¹0 when we only need to consider the case where q=0. [Jack, p.109, (3.59)] can be proved using [Mer, p.251, (11.98)] or [Coh, p.682, (30)]. [Jack, p.242, Fig. 11.3] helps explain the meanings of b and g in [Mer, p.111, (3.67)]. The proof in [Guo, pp.241-243, 5.14] is based on the same idea as Jackson's proof. For the first part of the proof, the explanation in [Jack, p.110, l.-17-l.-3] is better than [Guo, p.242, l.-6-p.243, l.8]. However, for the second part of the proof, the explanation in [Guo, p.243, l.9-l.-1] is better than [Jack, p.111, l.1-l.7].
- The Mittag-Leffler theorem.
To emphasize the purpose of the Mittag-Leffler theorem, [Guo, pp.17-20] shows that the theorem is an expansion theorem for meromorphic functions. However, from [Ahl, p.185, Theorem 4] the reader cannot obtain the required expansion except with luck. This is because g in [Ahl, p.185, l.-1] is undetermined. In other words, Ahlfors leaves the problem unsolved. Actually, the main part of Ahlfors' version of the Mittag-Leffler theorem turns out to be trivial for all the applications given in [Ahl, pp.187-188]. The significance of the Mittag-Leffler theorem lies in the specification of g in [Ahl, p.185, l.-1]. Thus, the way Ahlfors formulates the theorem shows that he only preserves its trivial part, leaving out its essential part. As for other authors of texts on complex variables, their formulations only keep the first part of [Ahl, p.185, Theorem 4] without considering the origin of its second part. This shows that these authors do not even know the purpose of the Mittag-Leffer theorem. For example, see [Ru2, p.291, Theorem 13.10]. In addition, the proof of [Ru2, p.291, Theorem 13.10] uses Runge's theorem, which is quite complicated. In order to facilitate understanding the essence of the Mittag-Leffer theorem, we should avoid such an unnecessary complication.
The proof of [Ahl, p.185, Theorem 4] [1] is effective because we may easily specify nn [Ahl, p.186, l.16]. If bn and Mn are given, we may select nn such that
limn®¥ Mn1/nn /|bn|=0 [Ahl, p.186, l.15]. For example, we may choose nn > log Mn [Ahl, p.186, l.16]. In contrast, it takes some effort to see that the proof of [Gon1, p.286, Theorem 4.3] is also effective. This is because González's formulation fails to provide the tracking information necessary to find bn [Gon1, p.287, l.1]. Based on the definition of uniform convergence, it seems that the existence of bn [Gon1, p.287, l.1] is hypothetical. However, if we investigate further and examine the proof of [Con, p.31, Theorem 1.3(c)], we will find that bn can also be specified once the principal part at an is given and the sequence {bi(n) | i=0, 1, 2, …} in [Gon1, p.286, (4.2-2)] is thereby completely determined.
Remark. Guo's proof [Guo, p.18, l.5-p.20, l.9] of the Mittag-Leffler theorem is most effective, but most of the time all we need to know for application is what the expansion is [Gon1, p.290, l.13] rather than how we can effectively obtain the expansion. Given a series identity [Gon1, p.288, l.-7], we may not know from where the identity comes and we do not want to know how we can effectively construct the identity from scratch. We simply want to use a theorem's statement to validate the identity regardless of the effectiveness of the theorem's proof. If this is the case, then the strategy and the method [Ahl, p.185, l.6-l.-12] instead of effectiveness become our top priority. The statement given in [Gon1, p.286, Theorem 4.3] would be sufficient for our purpose. [Gon1, p.287, l.-3] gives a neat description about the uniform convergence of [Gon1, p.286, (4.2-1)], while [Guo, p.21, l.-7-l.-6] does not. Now let us compare the effectiveness of Guo's proof with that of Gonzalez's proof. [Guo, p.17, (1)] is a strong hypothesis, so {jnp | n =1, 2, …} [Guo, p.18, (4)] have the same number of terms. In contrast, the number of terms that pn [Gon1, p.287, l.4] contains may vary with n. In [Gon1, p.286, l.4], gn is assumed known. One may wonder how one acquires this information in reality. The truth is that we deal with sophisticated cases primarily in theory, rarely in applications. The information is often derived from inspections or other simple means.¬¬
- The Weierstrass factorization theorem.
The Weierstrass factorization theorem serves to specify the expansion of a given meromorphic function in the form of an infinite product [Guo, pp.25-29, §1.7]. If the condition [Guo, p.17, (1)] is satisfied, then the required expansion is given by [Guo, p.27, (5); p.29, (7) & (8)]. In particular, if p=0 in [Guo, p.17, (1)] and we consider only an entire function with simple zeros, then the expansion will be reduced to a simpler form, [Guo, p.25, (1)]. The way that Ahlfors and Rudin formulate the Weierstrass factorization theorem [Ahl, p.194, Theorem 7; Ru2, p.325, Theorem 15.10] indicates that they do not know its origin.
Remark 1. If we want to expand a given entire function as an infinite product from scratch, we use [Guo, p.25, Theorem 1]. If the zeros and their corresponding orders are given and we want to find the function's general form or we want to prove the validity of a given identity, we use [Gon1, p.202, Theorem 3.16]. If we use [Guo, p.25, Theorem 1] instead, we have to do extra work: checking whether the given function satisfies the hypothesis given in [Guo, p.25, l.-10]. For example, [Guo, p.26, l.-10-l.-8; p.20, Example 1]. ¬¬
Remark 2. If a series is absolutely convergent, we may change the order of its terms or regroup the terms in any manner without changing the sum [Ru1, p.69, Theorem 3.57]. In contrast, for an infinite product, if it is absolutely convergent [Wat1, p.33, l.-10] and we regroup its terms, it may become not absolutely convergent [Wat1, p.33, l.-4]. However, we may restore its absolute convergence by adding some exponential factors [Wat1, p.34, l.9].
- Behavior at infinity [Sil, pp.242-245, chap. 11,
§58; Bed, p.379,
§117].
- Euler's homogeneous differential equation [Col, pp. 109-111, chap. II,
§6, subsection. 20].
- Existence of solutions about ordinary points
When a specific case is not equivalent to the general case, the conditions of the former are stronger than those of the latter. If a theorem's assumption changes from the general case to a specific case, we may find a more effective method to prove the theorem based on newly available sources. If not, it is only because we have not yet found an advantageous viewpoint. The proof given in [Guo, §2.2] is designed for the general case: a normal system of first-order differential equations. The proof given in [Jef, §16.03] is designed for the specific case: a second-order DE. Both proofs use the method of successive approximation, but the latter proof is more effective. The integration by parts given in [Jef, p.475, l.16] is a wise move. Via Jeffreys' approach we see that it suffices to prove the convergence of only one series [Jef, p.476, (13)] rather than two [Guo, p.50, (13)].
- Solutions of the DE in the vicinity of a singular point [Guo, p.55, l.5-l.14].
- The definition of analytic continuation has many versions, each of which serves a different purpose [Ru2, chap.16]. When discussing the solution near a singular point, the most appropriate definition of analytic continuation is given in [Bir, p.227, l.25]. The definition is clearly specified: there is no room for another interpretation. For other textbooks, one often wonders to which definition of analytic continuation they refer.
- When discussing the solution near a singular point, we must study the standard example first because the properties of the solution are quite similar to those of the standard example. This important standard example is discussed in [Bir, p.226, l.8-l.10; p.224, (2')].
- The form of A given in [Bir, p.231, l.15] can be derived by direct observation rather than by solving an algebraic equation [Guo, p.54, (13)].
- Generalization often obscures the key idea [Guo, p.51, l.-8]. All we need for an analytic continuation is its simple simulation [Bir, p.227, l.-21] rather than its formal definition. The failure to give a simple test [Bir, p.223, l.-5] for a branch point will make the concept of single-valuedness and multi-valuedness very confusing [Cod, p.108, l.-12 & l.-9]. These are reasons why the proof of [Bir, p.232, Theorem 4] clarifies the key idea of the method, while [Cod, pp.108-111, chap. 4, §1] does not.
- The fundamental theorem for a regular singular point [Guo, p.56, l.13-l.16].
- [Guo, p.58, (17)] produces a better estimate than [Bir, p.241, l.9] (Compare [Guo, p.59, (21)] with [Bir, p.241, l.20]).
- The proof of [Bir, p.240, Theorem 6] provides a clearer explanation than [Guo, p.57, l.1-l.3].
- [Col, pp.255-257, §15 & §16] gives a meaningful generalization without losing the big picture. [Bed, p.389, l.15-l.25] provides a more effective method of solving a differential equation whose indicial equation has a multiple root.
- The conclusions in [Guo, p.60, l.-7] is obtained from the experience of the calculation in [Bed, pp.369-371, §115]. On the one hand, a theory is synthesized from the practical experience of solving various differential equations. On the other hand, differential equations require a theory as a guide to classify them into various cases [Bed, §111-§116].
- In order to give the coefficients of a power series solution a closed form, we use the method in [Bed, pp.359-363, §113]. However, if we just want a good approximation for the solution, we prefer to find the recurrence relation using the method in [Bed, pp.365-368, §114].
- The Frobenius method [Guo, pp.61-63, §2.5].
It is better to use examples [Bed, §113 & §116] to illustrate the key idea behind the method. This because there are several problems with formulating the method into an advanced theorem:- A long passage [Guo, p.61, l.12-p.62, l.10] is required just to describe the setting of the theorem.
- The argument becomes vague when it comes to a subtle point, see [Guo, p.63, l.6].
- Some precious experiences can only be obtained from practical examples, but cannot be stressed in the form of a theorem [Bed, p.361, l.-6-l.-5; p.377, l.8-l.10].
- Fuchsian equations with three singularities [Bir, pp.251-254, chap. 9,
§13].
- [Bir, p.251, l.-14-l.-4] explains why we need to study the second order Fuchsian DE with three singularities.
- If we were to treat ¥ the same as the finite points in the extended complex plane, the argument and the calculations involved in proving [Guo, p.69, (3)] would be much simpler. See the proof of [Bir, p.253, (42)]. Guo first proves [Guo, p.68, (1)] and then lets c ® ¥. Guo's proof is unnecessarily complicated because he treats ¥ as an exceptional point in the extended complex plane.
- Prove [Wat1, p.207, (II)], where z = (Az1+B)(Cz1+D)-1.
Proof. By [Ru2, p.298, l.10-l.13], it suffices to prove that the equality given in [Wat1, p.206, l.22-l.24] remains the same form under the linear fractional transformation z1 = z-1. By the equality given in [Wat1, p.206, l.17],
2z-1 + (1-a-a')[az1(z1-a-1)]-1 + (1-b-b')[bz1(z1-b-1)]-1 + (1-g-g')[cz1(z1-c-1)]-1
= (1-a-a')(z1-a-1)-1 + (1-b-b')(z1-b-1)-1 + (1-g-g')(z1-c-1)-1.
Remark. The proof given in [Bir, p.251, l.16-l.22] is akaward.
- Irregular singularities.
- The origin of the form of normal solutions [Guo, p.74, l.4-l.-6].
- The Hermite equation [Guo, p.76, (16)] comes from searching for the normal solutions of the Weber equation [Guo, p.75, (11)].
Remark. [Coh, p.536, (15); p.537, (22); p.540, (43); p.541, (51)] provide the physical origin of the Hermite equation, but [Coh, chap. V] fails to point out the important role that the Hermite equation plays in the normal solutions for an irregular singular point.
- The gamma function [Guo, chap. 3].
- [Gon, p.615, Corollary 8.23] has the following two applications:
- [Guo, p.95, (10)].
-
The extension of
G(z) [Gon, p.615, l.-7].
Remark. Guo uses [Guo, p.97, (1)] to extend the domain of the gamma function [Guo, p.98, l.2], while Jeffreys uses [Jef, p.462, (6)] to extend the domain of the gamma function. It is easier to calculate the function value of the latter extension than that of the former one.
- Gauss' formula for y(z)
[Gon1, p.318, (4.6-26)].
Remarks. [Gon1, p.318, l.3-l.5] provides a simpler proof of [Gon1, p.318, (4.6-21)] than does [Wat1, pp.116-117, Example 6]. The proof of the first equality given in [Wat1, p.246, l.-6] can be found in [Guo, p.98, (4)]. [Ru2, p.33, Exercise 7] shows that Guo's approach given in [Guo, p.108, l.-9] is incorrect. - The beta function [Gon, pp.615-616, Theorem 8.47].
- Gauss' multiplication formula [Gon1, p.304, l.-11-p.307, l.1].
-
Hankel's formula [Wat1, p.245, l.-11]
The argument given in [Wat1, p.244, l.-8-l.-2] is consistent with the hypothesis given in [Guo, p.102, l.7] ( | arg (-t) | < p should have been | arg (-t) | £ p), but the argument given in [Guo, p.101, l.-7-l.-1] is not.¬ -
Stirling's
formula [Wat1, p.251, l.-6; p.252, l.2 & l.8]
The complete theorem concerning Stirling's formula is given in [Wat1, p.251, l.-8-p.252, l.10]. The estimate O( |z|-2n) given in [Guo, p.111, l.9] should have been O( |z| -(2n+1)). The constant O really depends on n, but the way Guo uses the notation O in [Guo, p.111, (2)] does not show this dependence. Therefore, [Guo, p.111, (2)] loses significant information contained in [Wat1, p.252, l.8]. As for [Lang1, p.277, G7] or [Gon1, p.320, (4.6-32)], they count only the first three terms in the asymptotic expansion of log G(z). Consequently, these two versions of Stirling's formula do not live up to the standard of high precision.¬
Remarks. Binet's second formula [Wat1, p.251, l.-6-l.-5] is proved in [Guo, p.122, (4)]. The series expansion given in [Wat1, p.251, l.-3] is proved in [Edw1, p.655, l.-12-l.-6]. [Wat1, p.251, l.-1] is proved in [Guo, p.120, (6)]. - The Hermite formula
[Guo, p.119, (3)] is obtained by changing the integrand in [Guo, p.117, l.-7] to j(z)[exp(2zi)-1]-1 and then changing the contour to that of its image reflected below the x-axis. Changing the contour alone cannot produce the desired result. The procedure stated in [Guo, p.119, l.5] is incorrect. - The Riemann z-function.
- The convergence involved in [Guo, p.123, (1)] can be proved by [Sak, p.433, chap. IX, Theorem 8.6(b)].
- [Gon, p.615, Corollary 8.23] has the following two applications:
- Infinite Processes.
- The Bolzano-Weierstrass Theorem.
In contrast with the proof given in [Sma, p.4, the Bolzano-Weierstrass Theorem], the proof of [Ru1, p.35, Theorem 2.42] appears very awkward. This is because [Ru1, p. 35, Theorem 2.41(b)] gives a more effective method than [Ru1, p.32, Definition 2.32] for checking whether a set is compact. - Dedekind cuts.
Dedekind cuts can be viewed in a rigorous way or in an intuitive way. The former view is good only for proving the completeness of the real line. Smail adopts the later view to prove the theorem in [Sma, p.5, §6]. In contrast, Rudin adopts the former view to prove [Ru1, p.11, Theorem 1.36]. All kinds of devices [Ru1, p.4, Definition 1.9; p.9, Theorem 1.32 (the generalization of the Dedekind cut of rational numbers to that of real numbers)] designed for proving completeness are used in this proof. Thus, by opening a Pandora's box, Rudin unnecessarily complicates his proof. - The convergence of a series.
- The tests of convergence:
- Simple tests [Sma, pp.73-77, §91-§100].
- Ratio test [Sma, p.78, §101].
- Root test [Sma, p.83, §103].
- Kummer's test [Sma, pp.86-87, §107].
- Raabe's test [Sma, p.88, §108].
- Dini's theorem [Sma, pp.90-91, Theorem 109].
- Cauchy's Condensation test [Sma, pp.91-92, §110].
- Maclaurin's integral test [Sma, pp.93-95, §111].
- Bertrand's tests [Sma, §113, §114, §116].
- Cahen's test [Sma, p.99, l.-5-l.-3].
- Gauss' test [Sma, p.101, §118].
- Errors [Sma, p.82, §102].
- Rapidity of convergence and divergence [Sma, pp.103-105, §120].
- The tests of convergence:
- The Bolzano-Weierstrass Theorem.
- Analytic continuation.
- The method for expanding the domain of an analytic function [Wat1, p.96, l.-17-p.97,
l.24].
Remark 1. The statement given in [Wat1, p.96, l.-12-l.-10] can be proved using [Ru2 p.224, Theorem 10.16].
Remark 2. It is more difficult to see the big picture of analytic continuation from [Ru2, p.347, l.-5-p.349, l.-10] than from [Wat1, p.96, l.-17-p.97, l.24]. Thus, in order to see the big picture, we should adopt a concrete setting to illustrate a method.- Using geometric series to expand a circular domain [Wat1, p.98, l.1-l.10].
- Using Borel's integral to expand a circular domain [Wat1, §7.81].
- How we construct an analytic function f in |z| <1 such that |z| =1 is the natural boundary [Ru2, p.344, Definition 16.3] of f [Wat1, p.98, §5.501; Ru2, p.347, Example 16.7].
- Uniqueness theorems
- Fix a chain. If an analytic function is given for the first circular disc, then the function for the last circular disc is uniquely determined [Ru2, p.348, l.8].
- Fix a curve g. If g starts at the center of the circular disk D, then (f, D) admits at most one analytic continuation along g no matter what chains cover g [Ru2, p.348, l.-3-p.349, l.1].
- The monodromy theorem [Ru2, p.351, Theorem 16.15]
Fix a simply connected domain W. Fix the start point and the end point of a family of curves in W. If an analytic function is given in the neighborhood of the start point, then the function in the neighborhood of the end point is uniquely determined no matter what what curve in the family is chosen.
Remark. [Wat1, p.97, l.-20-l.-8] is more confusing than [Ru2, p.351, Theorem 16.15]. Thus, in order to gain clarity, we should adopt an abstract setting (without using the Taylor series) to eliminate unrelated factors.
-
Application
Based on intuition, we think that the analytic continuation is only useful for nominal expansions, but fails to provide an effective method for calculation. For example, [Guo, p.102, (2)] is an analytic continuation of [Guo, p.93, (1)] and [Guo, p.151, (6)] is an analytic continuation of [Guo, p.136, (5)]. However, by combining the concept of analytic continuation with the knowledge of the form in [Guo, p.161, l.10], we can obtain [Guo, p.161, (8)] which greatly facilitates calculating the value of the hypergeometric function when |z| > 1.
- The method for expanding the domain of an analytic function [Wat1, p.96, l.-17-p.97,
l.24].
- Integral solutions versus series solutions.
- Why we need to represent the solution in an integral form [Guo, p.150, l.4-l.8; p.162, l.4-l.12].
- The basic principle of solving differential equations by integrals [Guo, p.78, l.9-p.80, l.10].
- Another advantage of integral solutions [Guo, p.84, l.-9-l.-8].
- Hypergeometric functions
- Classification of the solutions of the hypergeometric equation [Guo, §4.3]
- Barnes' contour integrals for the hypergeometric function [Guo, §4.6]
- Branch point at z = 1: Read [Wat1, p.291, l.3-l.5] and the section entitled "The Hypergeometric Function and Branch Points" of the following webpage:
http://mysite.du.edu/~jcalvert/math/complex.htm
Remark 1. Instead of using the hints given in [Wat1, p.290, l.-2-l.-1], I justify the interchange of the order of integration given in [Wat1, p.290, l.-8] as follows:
Use [Wat1, p.287, l.4; p.289, l.-9].
Let t = k+iv.
If k¹0, $d>0: p/2-d<|arg t|<p/2+d as v®±¥.
ts exp (-p|I(s)|) = O (exp (-(p/2)+d)|I(s)|)).
Remark 2. The equality given in [Wat1, p.291, l.3-l.5] can be proved as follows:
Proof. Let C- = [-i(N+1/2), i(N+1/2)] + S-, with S- : t = (N+1/2)eiq, p/2 ³ q³ -p/2, be the path of integration. Then let N®+¥. The poles of G(c - a - b - t)G(- t) lie on the right of the integration path and the poles of G(a+t)G(b+t) lie on the left. The right-hand side of the equality given in [Wat1, p.291, l.3-l.5] is the sum of the resides of the integrand at the poles of G(c - a - b - t)G(- t). - Branch point at z = ¥: Read [Wat1, p.289, l.3-l.5] .
- Branch point at z = 1: Read [Wat1, p.291, l.3-l.5] and the section entitled "The Hypergeometric Function and Branch Points" of the following webpage:
- [Guo, p.171, (5) & (6)] show that the generating function of the Jacobi polynomials is closely related to the Euler transform [Guo, p.88, (23)].
- The Chebyshev polynomial is a special case of the Jacobi polynomial [Guo, p.175, l.-6].
- [Guo, p.157, (5)] can be used to remove the restriction Re g> Re b>0. This removal is not only good for evaluating F(a,b,g,1) but also for extending the domain of F(a,b,g,z) [Leb, p.240, l.15-p.241, l.6]. In other words, it is good for dealing with the integral representation of a function closely related to the beta function [Guo, p.245, (9.4.3)].
- The formulation in [Leb, p.245, l.6-l.7] is more precise and concise than that in [Guo, p.153, l.-9-l.-7]. Furthermore, the former provides a proof, while the latter does not.
- Suppose we discuss a linear transform of the variable of the hypergeometric function. The use of the integral representation of the solution of the hypergeometric equation will cause a problem that requires justification [Lev, p.247, l.13]. If we directly relate the solution to the hypergeometric equation [Guo, p.70, (13)], then we can avoid this problem.
- Generalized hypergeometric series [Guo, pp.189-190, §4.15; Sma, p.102, Example (3); Luk, p.136, l.-7-p.137, l.2].
- Links: {1}.
- Legendre functions [Wat1, chap. XV; Guo, chap. 5]
- The generating function for Legendre polynomials [Guo, §5.3]
- Integral representations of Pnm : [Hob, p.188, (10)] if m+n is not a negative integer; factor (m2-1)m/2 should have added to the right-hand side of the equality given in [Hob, p.192, l.2-l.3] if m+n is a negative integer.
- Expressing Pnm in term of hypergeometric functions: [Guo, p.249, (8)] if m is not a positive integer; [Guo, p.250, (12) & (13)] if m is a positive integer.
- Definition of Qnm [Wat1, p.316, l.-25-l.-5;
Hob, chap. V, §125]
For |m|>1, Qnm is given by [Hob, p.195, (19) or p.196, l.7-l.13]. If n is not a positive integer, by analytic continuation, we can extend the domain of Qnm to the entire plane with the cut from +1 to - ¥ [Hob, p.195, (18); p.196, l.1-l.6]. If n is an integer, Qnm is given by [Hob,p.195, (20)].
Remark 1. The requirement R(n+1)>0 given in [Wat1, p.316, l.-9] is used to prove that the integrals along two small circles centered at -1 and 1 are small. For example, at t =1, the integral behaves like (reiq-1)n+1®0 as r®0.
Remark 2. Deriving the formula given in [Wat1, p.316, l.-7] from that given in [Wat1, p.316, l.-11]:
Proof. Qn = (4i sin np)-1(ò[-1, 1] (t2-1)n2-n(z-t)-n-1dt + ò[1, -1] e-2pin(t2-1)n2-n(z-t)-n-1dt).
Remark 3. [Guo, §5.8] introduces Qn by using the general formula given in [Guo, p.61, (27)]. Guo's method is tedious and fails to show the essential difference between the Legendre functions of the first kind and the Legendre functions of the second kind. In contrast, [Wat1, § 15.2; p.316, l.- 25-l.- 5] points out that their difference is determined by how the contour of integration surrounds the branch points of the integrand. In addition, Watson's method is much simpler. - Recurrence relations for Qn [Sne1,
pp.81-82, §19].
Remark. Giving a complete list [Guo, p.230, (1)-(5)] of recurrence relations for Qn is not as important as providing all the tools needed to prove these relations. Without proper tools, the readers may have problems overcoming the obstacles. - If y(x) is a solution of Legendre's equation, then (x2-1)m/2y(m) is
a solution of Legendre's associated equation [Sne1, p.86, l.10-l.18].
Remark. Mathematical discussion should speak of essence and should avoid empty words. For example, the direct substitution stated in [Guo, p.234, l.13-l.15] can easily lead to a mess in calculation. In contrast, [Sne1, p.86, l.10-l.18] provides a useful guide for avoiding such a mess. - Completeness: {Pn(x)} is a basis in
L2(|x|£
1) [Cou, vol. 1, p.82, l.-1]; {Ylm(q,
j)} is a basis in L2(x2+y2+z2=1)
[Guo, p.245, l.-5].
Remark. Completeness can be expression by the closure relation [Coh, pp.99-100, §d; p.665, (D-26)]. [Boh. p.324, l.11-l.14] treats the completeness of the surface harmonics as a postulate. It should be proved as a theorem. - Cnn [1; Wat1, §15.8; Guo, §5.23].
- Confluent hypergeometric functions [Lev, §9.9 & §9.10; Guo, chap.6].
- Derivation of the confluent hypergeometric equation
the hypergeometric equation [Guo, p.297, l.2]
® the equation given on [Guo, p.297, l.4] [replace z by z/b]
® [Guo, p.297, (1)] [let b=b®¥] - Derivation of the Whittaker equation
the confluent hypergeometric equation given on [Guo, p.300, l.-13]
® [Guo, p.300, (1)] [let y = ez/2z-g/2w(z)]
® [Guo, p.300, (1)] [let m = (g-1)/2, k = (g/2) - a] - Kummer's second formula [Wat1, p.338, l.-10]
Proof. e-z/21F1[m+2-1; 2m+1; z]=0F1[; m+1; z2/16] [Sla, p.12, (1.8.2)]
Remark 1. Ss=0t [(a)t-s(-1)s][(2a)t-s(t-s)!s!]-12-s
= [(a)t][(2a)t t!]-1Ss=0t [(1-2a-t)s(-t)s][s!(1-a-t)s]-12-s [because (a)t=(-1)s(a)t-s(1-a-t)s].
Remark 2. [Sla, p.12, (1.8.4)] follows from [Guo, p.179, (9)]. - In [Guo, p.304, l.-4-l.-1], Guo gives two proofs of [Guo, p.304, (8)]: a formal proof and a rigorous proof. Judging by the way he speaks, it seems that the formal proof is not a proof because it is not rigorous. In fact, a formal proof is the most direct, intuitive and effective proof because it avoids repetition (see [Guo, p.304, l.-2-l.-1]), but it requires justification. We can use [Ru2, p.27, Theorem 1.34] to justify the formal proofs mentioned both in [Guo, p.304, l.-4] and in [Guo, p.298, l.1-l.3] (see the series' uniform and absolute convergence in [Guo, p.136, (4)] and the integral's uniform and absolute convergence in [Guo, p.155, l.7-l.8]). Furthermore, by following the proof of [Guo, p.155, (9)], I find that [Guo, p.304, (8)] is valid in |arg(-z)|<p. The restriction |arg(-z)|<p/2 mentioned in [Guo, p.304, l.-5] is unnecessary. The proof of [Sla, p.37, (3.1.15)] does require the condition |arg(-z)|<p/2, but its contour of integration is different. The Cambridge publication provided this proof of Slater's in 1960. Slater's proof is only one point of view, not an authoritative one though, and it is outdated now. Studying science requires an independent judgment, not just copying someone else's result.
- The asymptotic expansion of Wk, m(z), when |z| is large [Wat1, §16.3].
Remark. [Guo, §6.6] provides two other proofs of the formula given in [Wat1, p.343, l.12]. - The second solution of the equation for Wk, m(z) [Wat1, §16.31].
- Mellin-Barnes contour integrals for Wk, m(z) [Wat1, §16.4]
- If k±m+1/2 is 0 or a positive integer, then the poles of G(-s-k±m+1/2) and those of G(s) may intersect [Wat1, p.343, l.-1].
- Prove the formula given in [Wat1, p.344, l.4].
Proof. Read [Guo, p.311, l.7-l.9]. - Prove the statement given in Wat1, p.344, l.5].
Proof. On the line s = it, |zs| = e(-arg z)t.
Combining it with the estimate given in [Wat1, p.344, l.4],
we have (the integrand given in [Wat1, p.343, (C)]) = O(e(|arg z|-(3/2)p)|t||t|-2k-1/2).
Consequently, the integral given in [Wat1, p.343, (C)] converges uniformly in {z| |arg z| £ (3/2)p - a}. - Prove the estimate given in [Wat1, p.344, l.-9-l.-8].
On the line s = -N-1/2 + it, |zs| = |z|-N-1/2 e(arg z)t.
By the method given in [Guo, p.311, l.7-l.9],
we have G(s)G(-s-k-m+1/2) G(-s-k+m+1/2) = O(|t|N-2k e(arg s -2p)|t|, where |arg s| £ (p/2) + d.
|zs| = |z|-N-1/2 e-(arg z)t, where |arg z| £ (3/2)p - a. - Prove that A=1 and that B=0 [Wat1, p.345, l.-12].
Proof. Let TN= 1+Sn=0N {m2-(k-1/2)2}…{m2-(k-n+1/2)2}/[n!zn].
I(z)/[e-z/2zk] = TN + O(z-N-1/2) [Wat1, p.344, l.-5].
Wk,m(z)/[e-z/2zk] = TN + O(z-N-1/2) [Wat1, p.343, l.8].
Hence (zN/[e-z/2zk])[I(z) - Wk,m(z)]®0 as z®¥ (*).
If B¹0, then the largest term of (zN/[e-z/2zk])[I(z) - Wk,m(z)] is BezzN-2k which approaches ¥ instead of 0 as z®¥. This contradicts (*). Therefore, B=0.
If A¹1, then the largest term of (zN/[e-z/2zk])[I(z) - Wk,m(z)] is (A-1)(zN/[e-z/2zk]) which approaches ¥ instead of 0 as z®¥. This also contradicts (*). Therefore, A=1.
- Prove the statement given in [Wat1, p.346, l.11-l.14].
proof. Let CR be s = Reiq, where -p/2£q£p/2.
On CR, Re (-s log s) is less than or equal to -2-1/2R log R +(p/[4´21/2])R if |arg s|£p/4 and
is less than or equal to (p/2)|Im s| if p/4£|arg s|£p/2.
[sec ps]2 = O(e-2p|Im s|). - Although there is no discrepancy between [Wat1, p.346, Example 2] and [Guo, p.314, (5)] when k is an integer, in terms of methodology the latter provides a better treatment.
is degenerated by the integration path s = reiq (-p/2£q£p/2), where r®0+. Note that this is different from the integration because a point can only contribute the value 0 to a Lebesgue integral. - Using the method of separation of variables to solve the Laplace equation in parabolic cylinder coordinates will lead to the Weber equation
[Guo, p.320, (1); Leb, pp.281-283, §10.1].
Remark. Notice the distinction between Lebedev's [Leb, p.281, (10.1.1); the vertical cylinder generated by a parabolic curve] and Landau's [Lan1, p.151, l.-6-l.-3; the surface of revolution generated by a parabolic curve] parabolic coordinates. - Prove that the integral given in [Wat1, p.349, l.12] is well-defined.
Proof. It suffices to prove the statement given in [Guo, p.83, l.-4].
-(p/2) £ arg (m+z) £ (p/2) - d.
Let p - d/2 £ arg t £ p. Then
(p/2)+(d/2) £ arg [(m+z)t] £ (3p/2)-d.
cos (arg [(m+z)t]) £ -sin (d/2).
|e(m+z)t| £e-|(m+z)t|sin (d/2).
- Derivation of the confluent hypergeometric equation
- Differentiations of vectors and tensors [Haw, chap. 11].
Remark. For the proof of [Haw, p.162, l.-1], see [Lov, p.80, l.11-l.13].
- Reduction of product representation [Hei, pp.67-71,
§9].
Remark. [Hei, p.69, l.-4] can be derived from [Coh, p.1028, (8)-(11)]. [Hei, p.69, l.-1] can be derived from [Coh, p.1029, (15)-(19)].
- Differential geometry.
- Prerequisite: [Fin].
Remark. This book provides a solid understanding of curves and surfaces of the second degree. After we finish reading this book, at least we will not call a hyperbolic paraboloid a hyperboloid [O'N, p.204, l.-15]. Their definitions and shapes are quite different. - Structures.
- Definitions of a topological manifold:
- Metrizable [Spi, p.624, Theorem 1].
- Second countable [Mat, p.97, Theorem 1].
- Definitions of a topological manifold:
- Essential contents.
- Local theory of space curves [Wea1, chap. 1; Kre, chap. 2].
- The explanation given in [O'N, p.56, l.-3-l.-2; p.57, l.1-l.3] is not as clear as that given in [Wea1, vol. 1, p.11, l.-14-l.-7].
- The definition of the osculating plane in [Wea1, p.12, l.-19] is not as rigorous as that in [O'N, p.61, l.15-l.16]. In addition, Kreyszig's three-point approximation [Kre, p.34, l.-7] is not as good as O'Neill's Taylor series approximation [O'N, p.61, l.12-l.13]. The latter method is not only simpler, but also leads to a stronger result. The three points described in [Kre, p.34, l.-7] are not only on a specific plane, but also on a specific parabola [O'N, p.61, l.12].
- It is important to relate the circular curvature to its circle [Wea1, vol. 1, p.13, l.8] as closely as possible [Wea1, vol. 1, p.13, l.8-l.21]. [O'N, p.62, Lemma 3.6] has done some related work, but not sufficient.
- Why does a minus sign appear in the formula B' = - tN? O'Neill says, "The minus sign is traditional [O'N, p.58, l.4-l.5]." His statement explains nothing. In fact, there are two things needing clarification. First, how do we interpret the sign of the torsion geometrically? The answer can be found in [Kre, p.38, l.-18-p.39, l.12]. Once we have this intepretation, we can ask the second question: Why do we have to put a minus sign in front of tN? The answer can be found in [Kre, p.37, Fig.11.1]. The interpretation given in [Wea1, vol. 1, p.14, l.-1-p.15, l.4] is very confusing.
- [Wea1, pp.21-23, §5] discusses the concept of contact only for a special case. In contrast, [Kre, pp.47-51, §14] symmetrically discusses the concept for the general case. Furthermore, the geometric meaning of contact of order m [Kre, p.47, Definition 14.1] is that the two curves intersect on m+1 consecutive points [Wea1, l.12, l.-20].
- Existence of curves with prescribed curvature functions [Kli, p.14,
Theorem 1.3.6].
Remark. The proof of [Kre, pp.42-45, Theorem 13.1] is much easier to understand than that of [Kli, p.14, Theorem 1.3.6] because the former is more concrete and includes more details. Although Klingenberg can see the big picture, he omits too many details. Omitting details indicates rashness, which is the root of mistakes and disorders. For example, [Kli, p.43, Corollary] is incorrect (see [Lau, p.53, Theorem 5.1.3]); the order of the two definitions in [Kli, p.44, Definitions 3.4.4] should have been reversed. - Suppose the parametric curves are orthogonal.
(a). The curves v=const. are geodesics Û E is a function of u only.
(b). The curves u=const. are geodesics Û G is a function of v only.
Remark. Although the statement given in [Wea1, vol. 1, p.101, l.14-l.17] is correct, the related statement that we often use is its converse.
- Local theory of surfaces.
- The normal curvature.
Remark. The geometric meaning of [Wea1, vol. 1, p.62, l.12] is similar [Wea1, vol. 1, p.59, l.10-l.17] to that of [O'N, p.61, l.4]. - The first (or metric) fundamental form of a surface [Lau, p.25, (3.17)].
Remark. The geometric proof, on the positive definiteness of the first fundamental form, given in [Wea1, p.54, l.4-l.6] is simple and intuitive. In contrast, the proof given in [Kre, p.70, (20.11)] is abstract because it is based on [Kre, p.17, (5.13)]. - Our knowledge of the shape of a surface comes from examining the normal curvatures of the curves on the surface [Lau, p.28, l.-12-l.-7; p.53, l.4-l.7].
- Fundamental theorem of surface theory (For the statement, see [Kli, p.64, l.-9-p.65,
l.3; Wea1, vol. 1, p.95, l.-2-p.96, l.2]; for the
proof, see [Lau, p.129, l.14-p.130, l.-7]).
Remark 1. (Integrability theory for systems of first order partial differential equations)
In [Spi, vol.1, p.252, l.4-p.253, l.11] Spivak shows that the integrability conditions for systems of first order partial differential equations have the same origin (the equality of mixed partial derivatives) as the integrability conditions for 1-form (2-dim: [Spi, vol.1, p.250, Proposition 0]; 3-dim: [Cou2, vol.2, p.104, the fundamental theorem]; n-dim: [Spi1, p.94, Poincaré Lemma]). The notations used in [Spi, vol.1, p.254, Theorem 1] and [Lau, Appendix II, §2] are quite similar. The similarity makes it easy for us to compare these two proofs. Note that in [Spi, vol.1, p.254, Theorem 1] fi is of class C¥, while in [Lau, Appendix II, §2] fa is of class C2. Spivak claims that there exist e1, e2 > 0 such that ("t1Î[-e1,e1]) ("tÎ[-e2,e2]) ([Spi, vol.1, p.256, (3)] holds). Treat t1 as a parameter (Spivak did not prove his claim correctly. We must use [Pon, p.170, Theorem 13] instead. This is the only way to prove [Spi, vol.1, p.254, Theorem 1]. Unfortunately, this important tool, [Pon, p.170, Theorem 13], is left out in [Arn1], [Bir], [Har] and many other popular textbooks in ordinary differential equations). Thus, Spivak solves a system of differential equations for each component of (t1,…,tm). In contrast, Laugwitz solves only one system of differential equations [Lau, p.226, (4)]. However, we must prove that yi(xb) is well-defined, more specifically that it is independent of the paths of integration [Lau, p.226, l.-14-l.-9]. Then the existence of a solution of [Lau, p.225, (1)] follows from the existence of a solution of [Lau, p.226, (4)]. For the proof of uniqueness, Laugwitz's consideration in [Lau, p.226, l.10-l.14] is insufficient, we need also take [Lau, p.226, l.-14-l.-9] into account. See [Spi, vol.1, p.254, l.-7].
Remark 2. (g~ij);k = 0 [Lau, p.130, l.14] can be proved using [Lau, p.118, Theorem 11.2.1].
Remark 3. The explanation given in [Kli, p.65, l.-10-l.-9] is clearer and more specific than that given in [Lau, p.130, step 3]. - Studying [Wea1, vol. 1, §62] requires the background given in [Fin, §§166-169; §§340-343].
- The normal curvature.
- Differential forms [Cou2, vol. 2, §3.6;
Spi, vol. 1, chap. 7]
- [Cou2, vol. 2, p.307, l.-7] links differential forms to an integrals, so we can understand the origin and purpose of differential forms. Note that òG L depends on the G and not on the particular parametric representation [Cou2, vol. 2, p.307, (55c)]. [Cou2, vol. 2, p.307, l.-7; p.323, (64c)] enable us to distinguish the dummy variables of integrals from the coordinates on a surface. [Cou2, vol. 2, p.317, l.2] links a differential form to a manifold. [Cou2, vol. 2, p.314, l.4-l.7] links differential forms to tensors. Actually, in [Spi, vol.1. p.282, l.1], a k-form on a manifold M is defined as a section of Wk(TM), i.e., an alternating covariant tensor field of order k.
- Spivak's approach to differential forms
Define Ám(V) [Spi, vol. 1, p.159, l.1] ® Define the tensor product TÄS [Spi, vol. 1, p.159, l.6] ® [Spi, vol. 1, p.275, Proposition 1 (1)] ® Define wÙh [Spi, vol. 1, p.275, l.-1] ® [Spi, vol. 1, p.279, Theorem 3] ® Use [Spi, vol. 1, p.282, l.4] to add a C¥-manifold structure on Wk(TM) ® Define a k-form on a manifold M as a section of Wk(TM) [Spi, vol. 1, p.282, l.1].
Remark 1. The inner product motivates us to define a symmetric 2-tensor [Spi1, p.77, l.17]; determinants motivate us to define alternating k-tensors [Spi1, p.78, l.9].
Remark 2. Ák(TM) is defined in [Spi, vol. 1, p.160, l.9]. - Poincaré Lemma
(1). Proofs. An open set star-shaped with respect to 0 [Spi1, pp.94-95]
® A manifold M smoothly contractible to a point [Spi, vol. 1, p.306, Corollary 18].
Remark. [Spi, vol. 1, p.321, Problem 23] links the above two proofs and shows that for a star-shaped domain we can solve w=dh explicitly in terms of integrals.
(2). Examples. 1-forms [1]; 2-forms [Spi, vol. 1, p.297, l.-10-l.-1].
(3). [Spi, vol. 1, p.298, l.11-p.300, l.3] shows that we can find a counterexample of [Spi, vol. 1, p.306, Corollary 18] if M is not smoothly contractible to a point.
- Integration of forms [O'N, chap. IV, Sec. 6]
- In Rn, we integrate a function on a volume. In a manifold M, we integrate a k-form on a k-chain [Spi, vol. 1, p.337, l.4-l.6].
- The fundamental theorem of calculus ® Stokes' theorem
on the integral of dw over a k-chain in an n-dim
manifold M, where
w is a (k-1)-form on M [Spi1, p.102,
l.13-l.20; Spi, vol. 1, p.345, l.5-l.6].
(1). Spivak relates the minus sign in [Spi, vol. 1, p.339, l.6] to the signed arrows in the third figure on [Spi, vol. 1, p.338]. This relationship leads nowhere. Only after we relate the minus sign to orientations [O'N, p.173, l.5] can we find a method to generalize the meaning of the minus sign to higher dimensions. - Stokes' theorem on the integral of dw over an oriented n-dim
manifold-with-boundary M, where
w is an (n-1)-form on M
with compact support [Spi1, p.124, Theorem 5-5; Spi, vol. 1, p.354, Theorem 6].
(1). The sum in [Spi, vol. 1, p.348, l.8] is actually finite [Spi, vol. 1, p.348, l.10].
Proof. Assume {p: f(p)¹0} Ç support w = Æ.
òM f×w = òc f×w, where support w Ì c([0,1]n)
= ò[0,1]n c*(f×w) = 0 [Spi1, p.90, l.2].
(2). In order to define òM w, we must stipulate that support w Ì the interior of c([0,1]k) [Spi, vol. 1, p.353, l.8-l.9]. This interior with respect to M contains points of in the image of c (n, 0) [Spi, vol. 1, p.353, l.9-l.10]. Consequently, ò¶M w in [Spi, vol. 1, p.353, l.11] is well-defined.
(3). The induced orientation on Rn-1´{0} = ¶Hn is (-1)n times the usual orientation [Spi, vol. 1, p.353, l.4].
When Spivak wrote [Spi1], he did not know how to prove this statement, so he treated it as a rule. The only justification he could give at that time was that Stokes' theorem will not have a neat appearance unless we adopt this rule [Spi1, p.119, l.-4-l.-3; p.124, l.11-l.22]. When he wrote [Spi], he finally be able to prove the above statement [Spi, vol. 1, p.353, l.1-l.4] using the properties of the determinant.
(4). In order to prove the the first equality in the line marked by (*) in [Spi, vol. 1, p.353, l.-3], we must note two things: First, support w = the closure of {p: w(p)º0 does not hold}. If w = f dx1Ù…Ùdxn, f(p)=0 may not make w(p)º0. w(p)º0 only if fº0 in a small neighborhood of p. Second, support w (the shaded area of the second figure on [Spi, vol. 1, p.353]) lies in a small neighborhood of a point on c(n, 0) and does not touch of the three other sides of the quadrilateral. In vector analysis, it is easy to visualize the divergence theorem [Wangs, §1-14]. In contrast, in differential geometry, it is difficult to visualize the proof of [Spi, vol. 1, p.354, Theorem 6] because the proof is divided into three segments: (a). Smoothly (using partition of unity) break the integral over a manifold into the sum of integrals over small parts. (b). For each small part, [Spi, vol. 1, p.354, Theorem 6] is the same as [Spi, vol. 1, p.343, Theorem 4]. (c). Smoothly reassemble the manifold with its small parts.
(5). Classical "Strokes' type" of theorems: [Spi1, p.134, Theorem 5-7; p. 135, Theorem 5-8 & Theorem 5-9].
In order to facilitate applications, we must translate Spivak's manifold versions into the fluid mechanics versions adopted by physics textbooks [Wangs, p.21, (1-59); p.24, (1-67)]. [O'N, p.170, Theorem 6.5] is Green's theorem [Spi1, p.134, Theorem 5-7]. [O'N, p.154, Definition 4.4] is essentially the equality given in [Spi1, p.134, l.-1]. - If nÎN is even, then there does not exist a nowhere zero vector field on Sn [Spi,
vol. 1, p.377, Corollary 15]. {1}.
Proof. Assume there is a nowhere zero vector field on Sn, then we can construct a homotopy between the antipodal map A and the identity map i. By [Spi, vol. 1, p.376, Corollary 14], deg A= deg i. However, by [Spi, vol. 1, p.373, Theorem 12] {1},
deg A = (-1)n+1 and deg i = 1. - The indices of the singular points of a vector field [Arn1,
§36]
(1). How we define the index of a curve [Arn1, p.309, l.15-l.18]
Remark. The index of a curve is a variant of the degree of f : S1 ® S1 [Dug, p.342, l.-13; 1].
(a). The index of a curve vs. the oriented basis of a vector space [Arn1, p.309, l.17-l.18].
(b). The index of a curve vs. the relationship between a domain and its boundary [Arn1, p.313, l.15-18].
(2). How the index of a singular point is related to the index of a curve [Arn1, p.312, l.-3-l.-1].
- Local theory of space curves [Wea1, chap. 1; Kre, chap. 2].
- Prerequisite: [Fin].
- How phase assignments to the logarithmic function affect the value of a contour integral.
For a confusing point, a good book will provide explanations with greater detail for clarity. In contrast, a bad book will omit the explanation and bog its readers down.
Example 1. Watson makes a vague explanation [Wat, p.166, l.15-l.17] of how he derives [Wat, p.166, (3)] from [Wat, p.166, (2)]. [Guo, p.369, (4)] is equivalent to [Wat, p.166, (3)]. However, Guo writes down [Guo, p.369, (4)] directly without any explanation. The following explanation may clarify the subtle point:
Watson's approach (compare [Wat, p.165, Fig. 5] with [Wat, p.165, Fig,4]): If we replace the second integral in [Wat, p.166, (2)] by the second integral in [Wat, p.166, (1)], what adjustment should we make? Originally, arg (t2-1) at B is -p. After the replacement, arg (t2-1) at B becomes +p. Therefore, we must add a factor exp (-2pi) for each factor (t2-1) to compensate for our replacement. In total, we must multiply the integrand by exp [-2pi(u-½)] for the adjustment because we have (t2-1)u-½. Finally, we have to multiply the integrand by -1 because the contours of the two integrals have opposite directions.
Guo's approach (compare the contour in [Guo, p.370, Fig.29; arg (t2-1) at Q is -2p] with that of the integral in [Guo, p.369, l.-3; arg (t2-1) at Q is assigned to be 0]): For the contour in [Guo, p.370, Fig.29], arg (t+1) is 0 at P and -p at Q; arg (t-1) is 0 at P and -p at Q. To understand this clearly, one must be able to evaluate arg (t+1) and arg (t-1) at every point A along the contour in [Guo, p.370, Fig.29] by counting how many turns the contour makes around -1 and +1 up to Point A respectively.
Example 2. Watson directly writes down the formula for Hu(2) in [Wat, p.170, l.12] without detailed explanation. In contrast, [Guo, p.371, l.4-l.12] gives more detailed explanation. Still, Guo fails to explain how he obtains the first term in the bracket in [Guo, p.371, l.8]. The reader might think his phase assignment is arbitrary and depends on his whim. Here I supply the following detailed reasoning to clarify the point:
Consider the starting point t=1+i¥. Originally, arg (t2-1)=-p. After replacing t2-1 by 1-t2, arg (1-t2) becomes 0. Therefore, we must multiply the integrand by exp (-pi) for each factor 1-t2 to compensate for the replacement.
Example 3 [Guo, p.250, l.-1]. A is the integral on the small counterclockwise circle around s=1; B is integral on the small counterclockwise circle around s=0. Let the contour in [Guo, p.249, Fig.13] intersect with the real axis to the right of s=1 at V1 and V2, where V1 is closer to s=1 than V2. Let the contour in [Guo, p.249, Fig.13] intersect with the real axis to the left of s=0 at U1 and U2, where U1 is closer to s=0 than U2. Now consider the small clockwise circle around s=1. Since arg V1 = arg V2 +2p (phases inherited from the contour in [Guo, p.249, Fig.13]), where V1(V2) is on the small clockwise (counterclockwise) circle around s=1), the value of su on the clockwise circle = e2upi ´ the value of su on the counterclockwise circle.
Example 4. If Im(m)>0, the value of the integral in [Hob, p.200, l.-8] equals Le-2npi-Me-2npi.
Proof. By the definition of M, the initial phase of t-1 at the starting point C is p [Hob, p.200, l.-15]. However, at the end point C of the contour (-1+, 1-), the phase of t-1 is -p.
Remark 1. To evaluate the phase of the integrand in a contour integral, we should not mix the assumptions with the consequences. Otherwise, we have to worry about the problem of consistency. For example, [Hob, p.184, l.-19-p.185, l.9] distinguishes the assumptions from the consequences, while the stipulation in [Guo, p.251, l.-1-p.252, l.5] fails to do so.
Remark 2. The rules of phase assignment:- To evaluate a contour integral, we must assign the phase of the starting point of the contour for each factor of the integrand.
- [Hob, p.184, l.-19-p.185, l.9] assigns the phases of m+1, m-1, t+1, t-1, t-m. All the assignments are based on one simple rule: ordinary assignment of a polar angle.
- [Hob, 192, Fig. (a) & (b)] shows that when we deform a contour continuously into another one and the deformation cannot avoid crossing a branch point, then the value of the contour integral may change. The two figures in [Hob, p.199] show a method of handling this type of problem. In the first figure the phase of t-1 at A is assigned to be +p because the entire contour is on the upper piece of the Riemann surface with the branch point +1. In the second figure the phase of t-1 at A is assigned to be -p because the entire contour is on the lower piece of the Riemann surface with the branch point +1.
- In [Hob, p.193, the right-most figure], we find a convenient point A and assign its phase relative to a branch point so that the phase of the starting point C relative to that branch point can be determined [Hob, p.193, l.-15].
- Binomial distributions.
- To introduce the Gaussian [Reic, §4.E.2] and Poisson [Reic, §4.E.3] distributions, Reichl emphasizes the conditions under which a binomial distribution becomes a Gaussian or Poisson distribution. In this way he provides an effective method of constructing the Gaussian and Poisson distributions and explains their origins. In contrast, [Lin, §3.2 & §3.3] just directly give the definitions of these two distributions without explaining their origins. Simply characterizing the properties of the Poisson distribution does not provide an effective construction of the limiting process. Lindgren's approach preserves the final answer, but leaves out the important constructing process. Thereby, his definitions of the Gaussian and Poisson distribution obscure their relationships to the binomial distribution.
- When Reichl defines [Reic, p.185, (4.34)], he may have a specific example [Reic, p.189, (4.40) & Lin, p.163, l.-6] in mind. However, because he fails to introduce that example before this definition, the definition becomes very hard to understand.
Quality checklist for a theory of tensors
- Does the theory distinguish a bound vector from a free vector? Good: [Kre, p.103, l.12-l.16]. Poor: [Pee, §8].
- Does the theory mention that the allowable coordinate transformations form a group? Good: [Kre, p.101, l.20-l.21]. Poor: [Pee, §8].
- Does the theory have a clear definition of a tensor field? Good: [Kre, p.111, l.12]. Poor: [Pee, §8].
- Does the theory have a consistent scheme for development? [Kre, (31.1), (31.2), (31.3) & (32.1)] are proved using the same scheme, while [Pee, p.230, (8.14)] is given by stipulation.
- Does the theory have a geometric interpretation for the contravariant or covariant components of a vector? Good: [Kre, p.116, Fig. 35.1 & Fig. 35.2]. Poor: [Pee, §8].
- When we use the elements of a vector space as contravariant vectors [Kre, p.121, l.-11-l.-10] and the elements of its dual as covariant vectors [Kre, p.123, l.10] to define tensors, do we relate it to the classical definition with a proper justification? Good: [Kre, p.122, l.9; p.123, l.-7-l.-6]. Poor [Spi, vol. 1, chap. 4].
- Intrinsic geometry.
To call Riemannian geometry intrinsic is an oversimplification. We must specify its details:- (Using intrinsic expressions) Using tensors to express physical quantities.
- (Using intrinsic generalizations) Generalizing intrinsic concepts.
Example. From the Gaussian curvature of a sphere [Ken, p.28, l.-3-l.-2] to the Gaussian curvature of a surface [Ken, p.30, (3.1)]. - (Using intrinsic calculations)
Example. From [Ken, p.28, l.-6] to [Ken, p.30, l.-10]. - Establishing theorems in intrinsic (tensor) forms.
- Parallel transport, in the sense of the connection of Levi-Civita, along a
path [Kre, pp.228-231, §78].
Remark. [Ken, p.215, A.6.1] gives a more rigorous proof of [Kre, p.231, (78.6)].
- Special surfaces.
- Envelopes; developable surfaces [Wea1, pp.38-65].
Remark. The examples given in [Kre, pp.254-255] further distinguish between the characteristic [Kre, p.253, (86.5)] and the intersection of nearby members of a family of surfaces [Wea1, p.40, l.-11]. - Minimal surfaces
- Descriptions of the local shape of a minimal surface
- Using the concept of the Gaussian curvature [Kre, p.236, l.-19-l.-18].
- Using the concept of minimum area [Kre, pp.236-237, Theorem 81.1].
- Using the concept of spherical mapping [Kre, p.238, Theorem 81.2].
- The global shape of a minimal surface [Kre, pp.244-245, Theorem 84.1].
- Ways to visualize a family of real minimal surfaces [Kre, pp.245-246, Theorem 84.2 & Theorem 84.3]].
- Descriptions of the local shape of a minimal surface
- Surfaces of constant Gaussian curvature and non-Euclidean geometry.
- The geodesic mapping of a pseudospherical surface into a plane [Kre, p.271, l.-14-l.-2].
- The geodesic mapping of a spherical surface [Kre, p.153, l.2] into a plane [Kre, p.271, l.-2-p.272, l.6].
- The surfaces with constant Gaussian curvature are the only surfaces that can be mapped geodesically into a plane [Kre, p.272, Theorem 91.1].
- Envelopes; developable surfaces [Wea1, pp.38-65].
- The curvature tensor
- Geometric interpretation of the curvature tensor [Kre, pp.292-295,
§100].
Remark. [Lau, p.107, Fig. 30] provides more information than [Kre, p.292, Fig. 100.1]. However, the argument given in [Lau, §10.3] is incorrect. - How a space with a vanishing curvature tensor simplifies the representation of an affine connection and the concept of parallel transport [Lau, p.109, Theorem 10.3.1].
- Geometric interpretation of the curvature tensor [Kre, pp.292-295,
§100].
- Bessel functions
- [Jack, p.426, (9.85); Guo, p.377, (4)] defines nl(z) to be (p/2z)1/2 Yl+½(z), while [Coh, p.947, (62-a) and (62-b)] use the definition nl(z) = - (p/2z)1/2 Yl+½(z).
- Expressing a plane wave as a linear superposition of free spherical waves [Coh, p.948, (65)].
- In order to introduce a special function, we should focus on its general properties. Consequently, we would like to use its integral representation [Guo, p.353, (5)] as its definition. The strategy for explaining the gamma function can be used as our blue print. The construction via the integral representation focuses on the locations of the function's singular points, its behavior at the origin and its asymptotic behavior [Coh, p.945, l.-5-p.947, l.15]. Then we endeavor to evaluate the function using its series representation [Guo, p.348, (7)].
- If n is not an integer, Jn and J-n are linear independent solutions of Bessel's equation [Wat1, p.359, l.7-l.9; Guo, p.348, l.8-l.10; p.365, (2)].
- Asymptotic series for Jn(z) when |z| is large
[Guo, p.378, (3), (4); p.379, (5), (6)]
The statement given in [Wat1, p.368, l.13-l.16] can be proved as follows: The asymptotic expansion of Wk, m given in [Guo, p.307, (2)] converges when |z|>1 [Wat1, p.24, l.18-l.19]. Therefore, the expansion is analytic in {z| |arg z|<p, |z|>1} and the ~ sign can be replaced by equal sign in {z| |arg z|<p, |z|>1}. This identity can be extended to the domain {z| |arg z|<3p/2, |z|>1}.¬ - If we fix n and consider Jn(z) as a function of z, then z = ¥ is a removable singularity [Guo, p.349, l.5-l.6; Wat1, p.368, l.-7-l.-5]. If we fix z and consider Jn(z) as a function of n, then n = ¥ is an essential singularity [Guo, p.348, l.9; p.349, l.7].
- If n is an integer, Yn is a solution of Bessel's equation [Wat, p.58, l.-17-p.59, l.9].
- The expansion of Yn in an asending series [Wat, p.62, (3)]
- Relations between Hankel functions and Whittaker functions [Guo, p.373, (16) & (17)]
- The zeros of Bessel functions whose order n is real [Wat1, p.361, l.10-l.11; l.14-l.15; Guo, p.422, l.7-l.8]
- Representations by continued fractions
- [Perr, p.300, l.3; p.299, (20)]
- [Inc1, p.181, l.-12-l.-9; p.180, l.-1]
- Fourier analysis of random processes [Matv, §14]
Remark. For detailed and rigorous definitions of a stochastic process, the power spectrum, the autocorrelation function, and stationarity, read [Fri91, §8.1, §8.2, §8.3].
- Asymptotic expansions [Wat1, §8.1 &
§8.2; Cod, §5.3].
- Definition of an asymptotic expansion [Wat1, p.151, l.5-l.11; Guo, p.30, l.3-l.15].
Remark. The side remark given in [Wat1, p.1151, l.11] should be removed from the definition. Otherwise, readers may mistake it for another condition to be satisfied.¬ - Uniqueness of an asymptotic expansion [Wat1, §8.32; Wat, §7.22]
The idea used to prove the statement given in [Wat1, p.154, l.1-l.2] can also be used to prove that the discrepancy between [Wat1, p.347, l.-7] and [Wat1, p.348, l.-3-l.-1] as well as the discrepancy between [Wat, p.201, (1)] and [Wat, p.201, (2)] is only apparent.
- Definition of an asymptotic expansion [Wat1, p.151, l.5-l.11; Guo, p.30, l.3-l.15].
- Even though the series given in [Wat1, p.252, l.-10] is the
asymptotic expansion of
f(x), the series diverges [Wat1, p.252, l.-3-l.-1].
However, the series can be used to estimate G(x)
[Wat1, p.253, l.3-l.8], solutions of ODEs with singularities of the
second kind [Cod, p.148, l.14-l.16] or other integrals [Inc1, §7.323]. Furthermore, there are cases that the use of
asymptotic series of J0(x) gives a more precise estimate than the use of its
convergent ascending series [Inc1, p.173, §7.321]. There are two important methods of
obtaining asymptotic expansions
- Method of steepest descents [Jef, §17.04]
- Features (Debye's observations): Saddle points [Jef, p.504, l.10-l.20;
Born, p.749, l.10-l.26]; paths of steepest descent [Guo, p.381, l.10-p.383, l.-3].
Remark. The fact that the real part of an analytic function has no maximum [Guo, p.381, l.22] can be proved by the statement given in [Ru2, p.259, l.-8-l.-7]. - Main result: [Jef, p.505, (18)].
- Features (Debye's observations): Saddle points [Jef, p.504, l.10-l.20;
Born, p.749, l.10-l.26]; paths of steepest descent [Guo, p.381, l.10-p.383, l.-3].
- Method of stationary phase [Jef, §17.05]
- Main result: [Jef, p.507, (10)].
Waston's lemma essentially says that ò[0,¥] e-zt f(t)dt is dominated by the values of f(t) in a neighborhood of t = 0 for large z and that we may estimate the integral by replacing f(t) with its local expansion for t = 0. - Method of steepest descents [Jef, §17.04]
- Asymptotic development of solutions [Inc1, §7.31]
Prove the statement given in [Inc1, p.171, l.6-l.7].
Proof. In [Inc1, §7.31], we need not worry about the convergence of series if we assume that p and q are analytic at x = ¥. Fix n.
u1+(u2-u1)+…+(un+1-un) = h+(C1/x)+…+(Cn-1/xn-1)+(Cn+e/xn) [Inc1, p.170, l.-6].
|(un+2-un+1)+(un+3-un+2)+…|<Mn+2[(K/x)+(K2/x2)+…] [Inc1, p.170, l.13]
<(K/x)n+1(2M2) = o(x-n).
Remark. "m>n" given in [Inc1, p.170, l.-11] should be replaced by "m ³ n-1".¬
Hamilton-Jacobi theory [Ches, §8-11]
Hamilton-Jacobi theory is the theory that discusses Jacobi's method [Sne, chap. 2, §§13-14] of solving first-order PDEs. The only way to understand the Hamilton-Jacobi theory is to consider it from the perspective of partial differential equations [Ches, chap. 8]. If you just read [Go2, chap. 10], [Lan1, §47] or any physicist's textbook on mechanics, you will never understand the theory's insight because these books fail to provide the important geometrical meanings of solutions of first-order PDEs. One often wonders how one can write equations like [Ches p.176, (8-34)] in mechanics given that x and p are related to each other somehow. This is because [Ches, p.176, (8-26)] is obtained by substituting u=p and w=q into F(x,y,u,v,w)=0. One also wonders how integration constants are related to parameters . This is also explained in [Ches, chap. 8] [1]. However, studying [Ches, chap. 8] requires some background in differential geometry [Wea1, chap. I-chap. IV]. The Hamilton-Jacobi equation [Lan1, p.147, (47.1)], derived from the consideration of mechanics, is a special case of the first-order differential equation [Ches, p.184, (8-61)]. Furthermore, [Ches, p.184, l.5-p.186, l.-4] shows that every first-order PDE can be reduced to a Hamilton-Jacobi equation [Ches, p.186, (8-72)]. Here I just highlight the geometrical meanings of Hamilton's equations and the Hamilton-Jacobi equation: the solutions of Hamilton's equations are the characteristics of the Hamilton-Jacobi equation [Ches, p.188, l.13-l.15]. For detailed construction, see [Ches, p.194, Theorem 8-2 & Theorem 8-3].
Remark 1. Jacobi's method is better than Charpit's method because it can be directly generalized to the case of n independent variables [Sne, p.80, l.1-l.11].
Remark 2. For the reason why one of the n+1 parameters is additive, [Lan1, p.148, l.13] gives a better explanation than [Ches, p.193, l.-14].- How we formulate differential equations on a Cr-manifold M.
- Endow the tangent bundle TM with the structure of a smooth manifold [Arn1, §34.2].
- If f : M ® N is Cr, define a corresponding Cr-bundle map f* : TM ® TN [Spi, vol.1, p.104, (c)].
- Define vector fields on M [Arn1, §34.5].
- [Arn1, p.304, Theorem, (1)].
Remark. In proving [Spi, vol.1, p.203, Theorem 5], Spivak fails to provide a concrete example for the proof. This makes it difficult for readers to see what is going on. In contrast, before Arnold proves [Arn1, p.304, Theorem] he gives a concrete example in [Arn1, p.303, l.-5-l.-2] to help readers see the big picture. - The geometrical meaning of [X,Y] [Spi, vol.1, p.218, l.-4-p.225, l.-1].
- Atlases of manifolds
- The sphere S2 [Arn1, p.291, Fig. 235].
- The projective space RPn [Arn1, p.291, Fig.237].
- The imbedding theorem in dimension theory [Mun, p.310, Theorem 9.6]
Note that the existence of the imbedding given in the proof of [Mun, p.310, Theorem 9.6] is logical [Wan3, p.109] because the proof uses Baire's category theorem. Only in special cases [Mun, p.305, Fig. 13] can the existence of imbedding be constructive.
- Separation theorems in the plane
- Nulhomotopy lemma: [Mun00, p.377, Lemma 61.2].
- Nonseparation theorems: [Mun00, p.389, Theorem 63.2; p.390, Theorem 63.3].
- The Jordan curve theorems: [Mun00, p.390, Theorem 63.4; p.392, Theorem 63.5].
Remark. [Mun00, p.390, Theorem 63.4] provides a big picture of [Dug, p.362, Theorem 5.4]. - Imbeding graphs in the plane: [Mun00, p.395, Lemma 64.1; p.396, Theorem 64.2; p.397, Theorem 64.4].
The winding number of a simple closed curve
- [Mun00, p.399, Fig. 65.2]. Proof. Use [Mun00, p.377, Lemma 61.2] and [Mun00, p.401, Theorem 65.2].
- [Mun00, p.404, Theorem 66.2].
- [Mun00, p.405, Lemma 66.3].
- The Seifert-van Kampen theorem
- [Mun00, p.426, Theorem 70.1] Þ [Mun00, p.431, Theorem 70.2] Þ [Mun00, p.368, Theorem 59.1].
- Link [1].
The orientation of a manifold
Nonsingular linear maps are divided into two groups: orientation preserving & orientation reversing [Spi, vol. 1, p.114, l.-5]
® An orientation of a vector space [Spi, vol. 1, p.116, l.3]
® An orientation preserving isomorphism from (V, m) to (W, n) [Spi, vol. 1, p.116, l.10]
® Assign the standard orientation on a trivial bundle en(X).
If X is connected, an equivalence f : en(X) ® en(X) is either orientation preserving or orientation reversing [Spi, vol. 1, p.116, l.-7].
® The above property (compatibility condition) of the trivial bundle can be used to define an orientation on a non-trivial n-plane bundle [Spi, vol. 1, l.-3]. Apply this definition to the tangent bundle of a C¥-manifold.The degree of of a continuous map f: Sn ® Sn is written D(f)
- D(f) is independent of triangulations of Sn [Dug, §XVI.1, Lemma 2 & Lemma 4].
- When n=1, D(f) = the winding number of f(S1) [Dug, p.335, l.-6-p.336, l.13]. [1].
- D(f) is a homotopy class invariant [Dug, p.339, Theorem 1.1].
- The degree of f: (Vn+1; Sn) ® (Vn+1; Sn) [Dug, p.340, l.4-l.-8]
- The degree of a proper map between two connected oriented n-manifolds [Spi, vol. 1, p.373, l.-1].
Remark. If one directly uses the advanced definition of the degree of a map given in [Spi, vol. 1, p.373, l.-1] without tracing back to its origins, then one will miss not only the concept's insightful meanings but also its step-by-step development.