Verifying Newtons 2nd Law For Rotation

Experimental Verification that t = Ia for a Rotating Disk

NAME_______________________________ PARTNER ______________________

DATE _______

INTRODUCTION

In the last lab, we used the definition of rotational inertia, I, to determine a theoretical equation for the rotational inertia of a disk. This equation was given by

Does this equation adequately describe the rotational inertia of a rotating disk system? If so, then we should find that, if we apply a known torque, t, to the disk system, its resulting angular acceleration, a, is actually related to the system's rotational inertia, I, by the equation

t = Ia or a =

PURPOSE

Part I: The purpose of this experiment is to determine if, within the limits of experimental uncertainty, the measured angular acceleration of a rotating disk system is the same as its theoretical value. The theoretical value of angular acceleration can be calculated using theoretically determined values for the torque on the system and its rotational inertia. Part II: The secondary purpose of this activity is to use Part I as the precursor for the introduction to a study of the Traditional Taiwanese Toy known as the Bamboo Dragonfly.

MATERIALS

The following apparatus should be available to you:

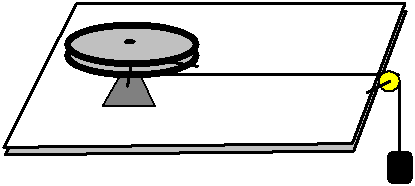
• A Rotating Cylinder System
• A 100 g or 50 g hanging mass
• A clamp stand to mount the system on
• String
• A meter stick and a Vernier calipers
• An MPLI Motion Detection System or other timing system
• A scale for determining mass

METHOD I : Theoretical Calculations

You'll need to take some basic measurements on the rotating cylinder system to determine theoretical values for I and t. Values of rotational inertia calculated from the dimensions of a rotating object are theoretical because they purport to describe the resistance of an object to rotation. An experimental value is obtained by applying a known torque to the object and measuring the resultant angular acceleration.

 

(a) Calculate the theoretical value of the rotational inertia of the disk using basic measurements of its radius and mass. Be sure to state units!

(b) Calculate the theoretical value of the rotational inertia of the hoop using basic measurements of its radius and mass. Be sure to state units.

(c) Calculate the theoretical value of the rotational inertia, I, of the whole system (disk and hoop). Don't forget to include the units.

(c) In preparation for calculating the torque on your system, summarize the measurements for the falling mass, m, and the radius of the spool. Don't forget the units!
Use the equation you above to calculate the theoretical value for the torque on the rotating system as a function of the magnitude of the hanging mass and the radius, rs, of the spool.

(e) Based on the values of torque and rotational inertia of the system, what is the theoretical value of the angular acceleration of the disk alone? What are the units?

Experimental Measurement of Angular Acceleration

Devise a good way to measure the linear acceleration, a, of the hanging mass with a minimum of uncertainty and then use that value to determine a. You will need to take enough measurements to find a standard deviation for your measurement of a and eventually a. Can you see why it is desirable to make several runs for this experiment? Should you use a spreadsheet? Then measure the accelerations of the disk, the hoop, as well as the disk and hoop together. If you have time you can also do the bar and the cylindrical masses.

Note: The value of a is not the same as that of the gravitational acceleration, ag.

If you choose to use a graphical technique to find the acceleration be sure to include a copy of your graph and the equation that best fits the graph. Also show all the equations and data used in your calculations. Discuss the sources of uncertainties and errors and ways to reduce them.

Compare your experimental results for a to your theoretical calculation of a for the rotating system. Present this comparison with a neat summary of your data and calculated results.

Summarize the theoretical and experimental values of angular acceleration.

Do theory and experiment agree within the limits of experimental uncertainty? How does the inertia of the spool affect the results?

Observation of the concepts of Angular Rotation, Torque, and Direction

Observing a Spinning Bicycle Wheel

You need:

 

• An old bicycle wheel mounted on an axle

Is Spinning More Stable?

(a) Do you expect it to take more torque to change the axis of rotation of a wheel that is spinning rapidly or one that is spinning slowly? Or do you expect the amount of torque to be the same in both cases? Explain.

(b) Hold the wheel axis along a vertical line while the wheel is not spinning and change the axis from a vertical to a horizontal direction. Describe the "torque" it takes qualitatively.

(c) Have someone help you get the wheel spinning rapidly while you hold the axle vertical. While the wheel is spinning change the axis to the horizontal direction. Describe the "torque" it takes qualitatively. How does the torque compare to that needed to change the direction of the axis of rotation of the wheel when it is not spinning? Did you observe what you expected to observe?

(d) Does the magnitude of the angular velocity vector change as you change the axis of rotation of the wheel? Does its direction change? Does the angular velocity vector change or remain the same? Explain.

(e) Does the angular momentum vector change as you change the axis of rotation of the spinning wheel? Why or why not?

1. If possible use your answer to part (e) above to "explain" what you observed in part (c) above.

METHOD II: Taiwanese Bamboo Dragonfly

Experimental Design

The procedural component of this activity is not to follow a step-by-step approach, but rather to utilize previous knowledge and laboratory experiences to design a technique for experimentation with the Bamboo Dragonfly. There are two fundamental types of Bamboo Flyers. One is based on simply placing the propeller shaft in the palms of your hands and quickly creating the appropriate torque to generate a large enough angular velocity to create an unbalanced condition of pressures above and below the propeller blades to create lift.

The second is a smaller bamboo shaft with propeller placed inside a larger diameter hollowed bamboo shaft. A string is wrapped around the propellered shaft that can then pulled with a Force (F) that should be measurable. The second form of the Bamboo Dragonfly is similar in many ways to the condition of rotation that is exemplified by the rotational motion of the bicycle wheel around a vertical axis. We should be able to:

 

1. Draw a free body diagram showing the forces acting on the smaller bamboo shaft with mass, m, in terms of m, a and FT.
2. If the magnitude of the linear acceleration of the mass, m, is measured to be a, what is the equation that should be used the calculate the tension, FT, in the string (i.e. what equations relates m, FT and a)? Note: In a system where FT - mag = ma, if ag<<a then FT = ma.
3. What is the torque, ?, on the shaft-axle-propeller system as a result of the tension, FT, in the string acting on the shaft?
4. What is the magnitude of the angular acceleration, a, of the rotating system as a function of the linear acceleration, a, of the mass and the radius, rs, of the shaft?
5. If the rotational inertia of the axle and the shaft are neglected, what is the rotational inertia, I, of the propeller of radius rp as a function of the torque on the system, t, and the magnitude of the angular acceleration, a?
6. What is the theoretical value of the rotational inertia, Ip, of a propeller of mass M and radius rp in terms of Mp and rp?

ANALYSIS / CONCLUSIONS

• What general observations can you make about the two types of Bamboo Dragonfly?
• What happens when you spin the flyer in opposite directions?
• Discuss the Physics involved in the Bamboo Flyer. Explain all aspects of rotation.
• Discuss the physical concept of flight for the Bamboo Dragonfly, as well as, the relationships to fluid pressure.
• Using the second version of the Dragonfly, run a set of observation trials with a slow pull of the connector string, a moderate pull for a second trial and fast pull of the connecting string as a third trial. How does the speed of the pulled string affect the bamboo flyer? How can you use the ideas and concepts of linear and angular motion to describe qualitatively and quantitatively the concepts involved in the Bamboo Dragonfly?
• Things to think about - How could we change the design to enhance the flyer? Generate questions along the "What would happen if.." concept of thinking. What devices do you know of that use the same concepts shown by the Bamboo Dragonfly? Compare the function of the Dragonfly blades to the blades of a helicopter. How can experimentation with the Bamboo Dragonfly demonstrate the principles of conservation of energy and linear and angular momentum?