Sound

RESONANCE: THE SPEED OF SOUND AND MUSIC GRAPHS

NAME_______________________________ PARTNER ______________________ DATE _______

INTRODUCTION

Resonance, or sympathetic vibration, occurs when the natural vibration rates of two objects are the same or small whole number multiples. The air column in a closed glass tube produces its best resonance when it is approximately one-fourth as long as the wavelength of the sound that it reinforces. For example, a tube one-meter long produces resonance with a sound wave that is about four meters long. A small correction in wavelength must be made for the internal diameter of the tube. The wavelength of the sound may be calculated from the resonant length of the tube by using the equation l = 4L +KD, where l is the wavelength, L is the length of the resonant column of the closed tube, and D is the diameter of the tube and K is some number that is experimentally determined. In this experiment the best resonant length of a closed tube will be determined. From this length and the diameter of the tube, the wavelength of the sound will be calculated. The speed of sound will then be calculated from the equation v = f l , where v is the speed of sound, f is the frequency, T = = Period, and l is the wavelength. Substituting the above equations you can show that 4L = vT - KD.

PURPOSE

After completing this experiment, you should know how to determine the resonant length of a closed tube for a known frequency and to use this technique for determining the speed of sound in air of known temperature. You will also gain experience with interface data acquisition and analysis of wave patterns (FFT patterns) for a variety of Traditional Musical Toys found in the cultures of our TAS students.

MATERIALS

Several tuning forks, 256 Hz to 512 Hz., glass resonance tube, 2.5 cm to 4.0 cm in diameter and at least 40 cm long, tall cylinder, thermometer, meter stick, inside calipers or metric Vernier calipers, tuning fork hammer or large rubber stopper on chopstick, assortment of musical toys and instruments, MPLI or ULI interface, microphone/amplifier (Vernier), and sound FFT software for interface

PROCEDURE

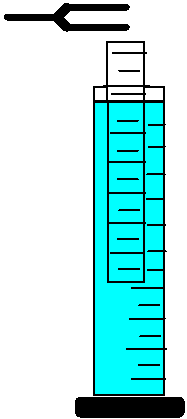
PART I Speed of Sound

To set a tuning fork vibrating, hold it and strike it on a large rubber stopper or soft book. Suggestion: A few practice strikes may be helpful to distinguish the tonal sound of the fork from the unwanted metallic "ringing" sound that may result from an overly severe strike. Hold the tube vertically in a cylinder nearly full of water. Set the tuning fork to vibrating (do not strike the fork on the table top or other hard surface) and, while holding the vibrating fork over the open end of the glass tube, slowly raise and lower the tube in the water until a position is located where resonance produces the loudest sound.
Then, hold the tube firmly in the optimum resonance position while another student measures the length of the air column from the top of the tube to the water surface inside the tube. Record this length to the nearest thousandth of a meter (nearest millimeter) in the data table.
Carefully measure the internal diameter of the tube to the nearest millimeter.
Also record the temperature of the air inside the tube to the nearest 0.5-degree.
Collect and record data for five trials, using forks of different frequencies.
Sound the tuning fork and hold it in the air; roughly time how long you can hear it. Then sound it again but put the base of the fork firmly on the lab table and again estimate the time you can hear it.
Optional Extra: Measure the speed of sound in another way that is as accurate as this method.

DATA

FREQUENCY

RESONANT LENGTH

Period =1/f

4L

DIAMETER

TEMPERATURE

PART II Music Graphs

Bring musical toys or instruments to class.
Set up the computer to record oscillograms of sounds.
Agree with your lab partner to play the same musical note on different instruments; tune your instruments to the same pitch. If using toys try using similar toys
Record both musical toys and instruments on separate graphs. Also produce the FFT (Fast Fourier Transform) for each toy or instrument. Use the cursor to find the frequency of each of the main harmonics played by each toy or instrument. Print your four graphs and write the frequencies of the harmonics on the graph and identify them as 1st, 2nd, etc.
Record (but don't print) graphs of some other toys or instruments. Are the FFT patterns similar?

ANALYSIS / CONCLUSION

1. Make four columns in Excel: f, L, Period, 4L, then type the data and use formulas to fill in the last two columns. Plot the values of 4L (y-axis) as a function of Period (x-axis).

2. Find the slope and intercept of the graph to the proper number of significant figures. From the slope find the speed of sound. From the intercept find KD and then K= the diameter correction factor.

3. Calculate the speed of sound from the temperature and the accepted value of the speed at 0.0 degrees. v = (331.5 + 0.59 Tc) m/s. Compare the speed from the graph with that calculated from the temperature.

4. If we ignore the correction for the diameter of the tube the resonant length is approximately 4L. We could easily vary the length of the tube that was closed on one end. Suppose we had tubes open on both ends. How would you experimentally find the resonant length of these open pipes? The resonant length is like a string where L = (l /2).

5. Compare the wave patterns of the various Musical Toys and identify any apparent relationship between the waveform produced as the frequency and amplitude are changed. Can you find another toy similar to the one's you tested that have nearly the same frequency? If so, redo an oscillogram for the two sounds of nearly the same frequency and see if a beat pattern is produced. Record any observations.

6. Write a paragraph comparing the sounds of various musical toys or instruments, including at least the two you tested in part II. You may have to look at other students graphs for different toys and instruments. With some research you might find similarities between certain types of toys and instruments. There is a CD-ROM called "Musical Instruments" available for you to use. You could also compare a real instrument to a synthesized sound of the same instrument.