The Perpendicular Distance between a given Point and a given Plane

Problem: Find the perpendicular distance between the point given by the position vector [3, 1, 5] and a plane which has; a normal parallel to the vector [0, 4, 3] and, a perpendicular distance from the origin of 2.
A diagram of this is shown on the right.		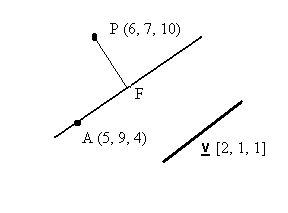P is the given point. OP is the position vector of the given point. The disc is a section of the plane. ON is the normal to the plane which passes through the origin O. n is the given vector to which the normal ON is parallel. M is the point where ON crosses the plane. F is the point where the perpendicular from P meets the plane. FP is the required distance.
A line is drawn from P, parallel to the plane and hence, at rightangles to ON, meeting ON at Q.		Since FP and ON are both perpendicular to the plane and PQ is parallel to the plane then, MQ = FP. Therefore, the length MQ is equal to the required distance.
By inspection, MQ = OQ - OM	OM is the perpendicular distance of the plane from the origin. This distance is given in the problem as 2. OM = 2 OQ is the projection of the vector OP on to ON which is parallel to the vector, n = [0, 4, 3] OQ is then, the scalar (dot) product of OP and the unit vector = ; OQ = [3, 1, 5]. = We can now, finaly calculate MQ using; MQ = OQ - OM = - 2 = 1

HOME

The Perpendicular Distance between a given Point and a given Plane

Problem:Find the perpendicular distance between the point given by the position vector [3, 1, 5] and a plane which has; a normal parallel to the vector [0, 4, 3] and, a perpendicular distance from the origin of 2.

Problem:

Find the perpendicular distance between the point given by the position vector [3, 1, 5] and a plane which has; a normal parallel to the vector [0, 4, 3] and, a perpendicular distance from the origin of 2.