SpaceTime Around Kerr's Rotating Black Holes.
Kerr's rotating Black Holes.
Let's generalise some of the formulas used in the static Schwarzschild case, to the case of rotating Black Holes. The Kerr metric is written in Boyer-Lindquist coordinates: 
where the coordinate functions are given (with G=c=1):
the specific angular momentum is:
The physical value of J is for a star like the sun:
corresponding to a=0.185 M.
If a=0 we have the Schwarzschild case for a nonrotating Black Hole (or star).
We define FIDucial Observers (FIDOs) as little (experimental) physicists locatedat each point in spacetime measuring all possible physical quantities in their local proper units. They'll get a hard job in the Kerr geometry. To keep their job, they have to follow the geometry which actually rotates with increasing speed towards the center. How can this be? All physical objects are dragged into circular motion by the Black Hole's rotation. Our FIDOs (which are supposed to be at rest) will follow the (absolute) space around the rotating hole. The Boyer-Lindquist coordinates naturally includes this rotating coordinate system, so in the Kerr reference frame, the geometry actually swirls like the air in a tornado. The angular velocity of a FIDO as viewed from infinity is:
This angular velocity depends on a and r. The larger a, the larger 
.
[The coordinate system rotates with the hole (because of ).
One straight radius is deformed into a spiral after some time. From left to right: a=0,0 and a=1,0.]
Other properties of the Kerr metric:
The redshift factor 
is generalised with the coordinate functions to:
The Kerr metric has two horizons instead of one, and a static limit inside which nothing can remain at rest (there's only one way around: with the rotation):
- The inner horizon:
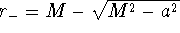
- The outer horizon:
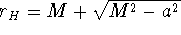
- The static limit:
and the static limit is called the
ergosphere.
The curvature will just change with 
as:
Now we can show the angular (time dependent) rotation with the curvature.
Visualizing rotating coordinates:
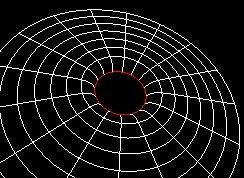
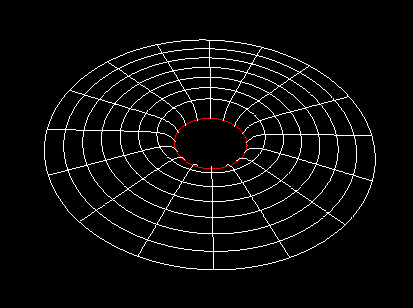
Within the Inventor/VRML language, it is possible to divide the polar plane into stripes, where each mini-radius (a discrete element) rotate with increasing angular velocity inwards. When a grows, the horizon gets smaller, and the curvature greater. Therefore the extreme Kerr (a=1) case has a quite bigger curvature surface than the static Schwarzschild case.
Rotation: a=0.0
[The red circle marks the Schwarzschild horizon at r=2M.]
Rotation: a=1.0
[The red circle is the extreme Kerr horizon at r=1M.]
Rotation from 0.0 to 1.0
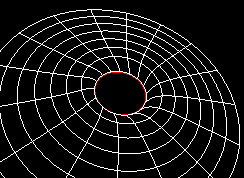
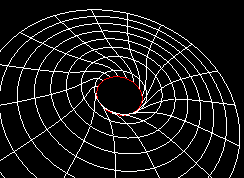
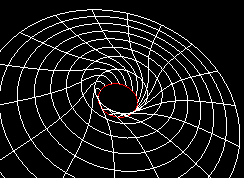
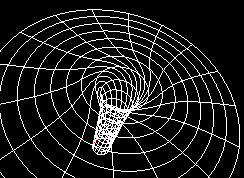
[Pictures from a series of curved coordinate sytem with 'frozen'
rotation. The greater value of a, the more wickled does the radial
lines get. It is like the water in a whirlpool, or the air in a tornado!
The original 3D-Inventor/VRML files can be seen below.]
Inventor-files (*.iv): a=0.0 a=0.2 a=0.4 a=0.6 a=0.8 a=1.0
VRML-files (*.wrl): a=0.0 a=0.2 a=0.4 a=0.6 a=0.8 a=1.0