A relatividade da distância
A distância não é uma grandeza absoluta, mas depende do movimento do corpo em relação a um dado sistema de referência.
Designemos por 
o
comprimento de uma vara no sistema de referência K, em relação
ao qual a vara está parada. Então o comprimento 
, desta vara, no sistema k1 , em relação ao qual
a vara se move com velocidade v, determina-se pela fórmula.
Como se vê por esta fórmula ,
.
Nisto consiste a redução relativista do corpo nos sistemas de referência em movimento.
Relatividade dos intervalos de tempo.
Seja o intervalo de tempo entre dois acontecimentos que se dão no mesmo ponto do sistema inercial K igual a t 0 . Tais acontecimentos podem ser, por exemplo, dois batimentos de um metrônomo que conta os segundos.
Então o intervalo t entre estes acontecimentos, num sistema de referência k1 , que se move em relação ao sistema K com a velocidade v, exprime-se do seguinte modo.
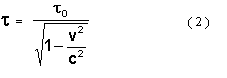
Evidentemente t
> t 0 .
Trata-se do efeito relativista de atraso do tempo nos sistemas de referência
em movimento.
Se tivermos v <<
c , nas fórmulas ( 1 ) e ( 2 ) pode desprezar-se a grandeza
v2 / c2 . Então será
ou seja, a redução dos corpos e o atraso do tempo relativistas num sistema de referência em movimento podem não ser tomados em consideração.
A lei relativista da composição das velocidades. Aos novos conceitos relativistas de espaço e de tempo corresponde uma nova lei da composição das velocidades. Evidentemente que a lei clássica da composição das velocidades não pode ser verdadeira, visto que ela contradiz a afirmação de que a velocidade da luz é constante na vácuo.
Se um comboio se move com a velocidade v e num vagão, segundo a direção do movimento do comboio, se propaga uma onda luminosa, então a sua velocidade em relação á Terra deve ser igual de novo a c , e não a v + c . A nova lei da composição das velocidades deve conduzir ao resultado pretendido.
Formularemos a lei da composição das velocidades para o caso particular em que o corpo se movimenta ao longo do eixo X1 do sistema de referência K1 , o qual, por sua vez, se move com a velocidade v em relação ao sistema de referência K. Além disso, os eixos das coordenadas X e X1 coincidem sempre, enquanto os eixos das coordenadas Y e Y1 , Z e Z1 se mantêm paralelos (fig. 4) .
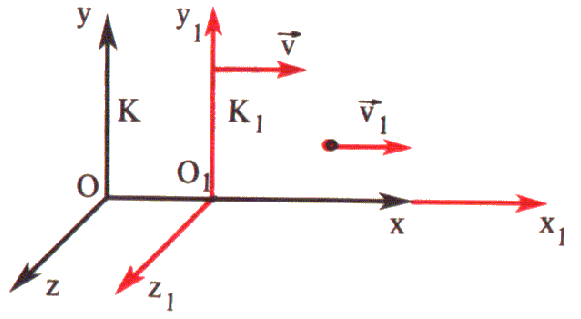
Fig. 4
Representemos a velocidade do corpo em relação a K1 por v1 , a velocidade do mesmo corpo em relação a K por v2 . Então, de acordo com a lei relativista da composição de velocidades,
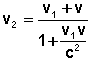
Se v << c e v1 << c , então podemos desprezar o termo v1 v / c2 no denominador e, em vez de ( 3 ) , obtermos a lei clássica da composição das velocidades:
v 2 = v 1 + v
Quando v1 = c , a velocidade v2 também se torna igual a c , tal como exige o segundo postulado da teoria da relatividade . De fato,
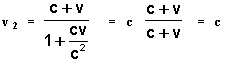
Uma admirável propriedade da lei relativista da composição de velocidades consiste em que, para quaisquer velocidades v1 e v (evidentemente, não superiores a c ) a velocidade v2 não é superior a c . No caso limite em que v1 = v = c obtém-se
PARTE II
No caso de grandes velocidades, as leis da mecânica de Newton não estão de acordo com os novos conceitos de espaço e de tempo. Só quando a velocidade é pequena e os conceitos clássicos de espaço e de tempo são válidos, a segunda lei de Newton
não se altera com a transição de um sistema de referência inercial para outro (verifica-se o princípio da relatividade).
Para a velocidades grandes, porém, esta lei, na sua forma habitual (clássica), não é verdadeira.
De acor do com a segunda lei de Newton ( 4 ) uma força constante, que atue no corpo durante algum tempo, pode transmitir-lhe uma velocidade tão grande quanto se queira. Mas na realidade, a velocidade da luz no vácuo é limitada, e em nenhumas condições um corpo pode mover-se com uma velocidade maior do que a velocidade da luz no vácuo. É necessária uma pequena mudança na equação do movimento dos corpos para que ela se torne verdadeira para grandes velocidades do movimento. Passemos previamente à formulação da segunda lei da dinâmica, utilizada pelo próprio Newton:
onde
é o impulso ( quantidade de movimento) do corpo. Nesta equação, a massa do corpo considerava-se independente da velocidade.
É surpreendente que mesmo no caso de grandes velocidades a equação ( 5 ) não muda de forma. As modificações só dizem respeito à massa. Quando aumenta a velocidade do corpo a sua massa não se mantém constante, mas aumenta. O aumento da massa é tanto mais acentuado quanto mais perto a velocidade do corpo estiver da velocidade da luz c .
A dependência da massa em
relação à velocidade pode calcular-se a partir da
suposição de que a lei da conservação do impulso
é verdadeira para as novas concepções de espaço
e de tempo. Os cálculos são demasiado complicados. Apresentemos
apenas os resultados finais.
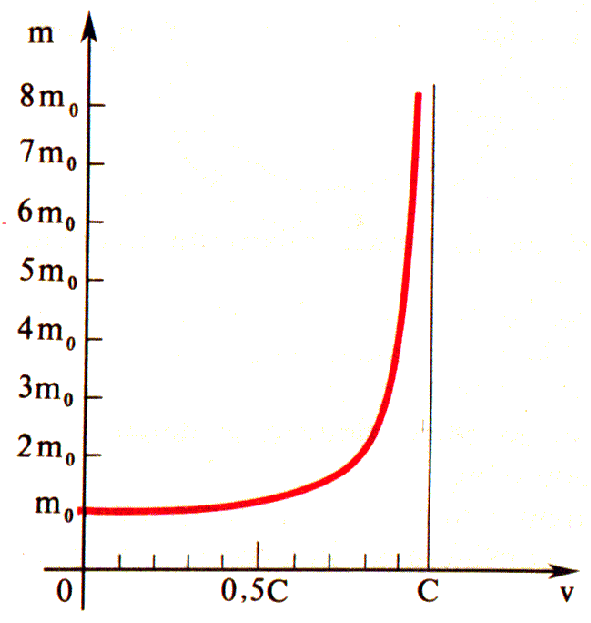
Fig. 5
Se designarmos através de m0 a massa do corpo em repouso, então a massa m deste mesmo corpo em movimento com velocidade v define-se pela fórmula
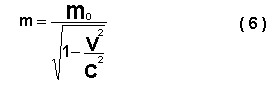
Na figura ( 5 ) está representada a dependência da massa do corpo em relação à sua velocidade.
Quando a velocidade do movimento é muito menor
do que a da luz, a expressão
pouco difere da unidade. Assim, para a velocidade de uma nave espacial atual, v » 10 km/s , obtemos:
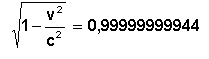
Não é de admirar, por isso, que não se note o aumento da massa com o aumento da velocidade quando comparamos pequenas velocidades. Mas as partículas elementares, nos atuais aceleradores de partículas carregadas, atingem velocidades enormes. Se a velocidade de uma partícula for apenas 90 km/s menor do que a velocidade da luz, então a sua massa aumenta 40 vezes. Os aceleradores potentes de elétrons podem imprimir a estas partículas velocidades inferiores à velocidade da luz apenas em 35 - 40 m/s. Nestas condições, a massa do elétron aumenta aproximadamente 2000 vezes e torna-se maior que a do próton. para que este elétron se mantenha numa órbita circular é necessário que o campo magnético exerça sobre ele uma força 2000 vezes maior do que se poderia supor, não considerando a dependência de massa em relação à velocidade. Para calcular a trajetória de partículas rápidas já não se pode utilizar a mecânica de Newton.
De acordo com a relação ( 6) , o impulso de um corpo é igual a:
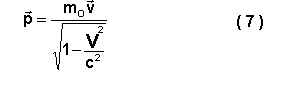
A lei fundamental da dinâmica relativista mantém a forma anterior
No entanto, o impulso do corpo
neste caso define-se pela fórmula ( 7 ), e, não pelo simples
produto 
.
Deste modo, a massa, que desde o tempo de Newton, durante dois séculos e meio, se considerava invariável, na realidade depende da velocidade.
À medida que aumenta a velocidade, a massa do corpo, definida pelas suas propriedades inerciais, aumenta. Quando v ® c, a massa do corpo, de acordo com a equação ( 6 ) cresce ilimitadamente ( m ® ¥ ) ; por isso, a aceleração tenda para zero, e a velocidade praticamente deixa de aumentar, por mais que se prolongue a ação da força.
A necessidade de utilizar a equação do movimento relativista, quando se calcula a aceleração de partículas carregadas, significa que a teoria da relatividade, no nosso tempo, passou a ser uma ciência estreitamente ligada à engenharia.
As leis da mecânica de Newton
podem ser consideradas um caso particular da mecânica relativista,
sendo verdadeiras quando a velocidade do movimento do corpo é muito
menor do que a velocidade da luz.
PARTE III
Passemos agora a uma importante conseqüência da teoria da relatividade, que desempenha um papel essencial na física nuclear e na física das partículas elementares. Falaremos sobre a relação universal entre a energia e a massa.
A relação entre a energia e a massa resulta da lei da conservação da energia e do fato de a massa do corpo depender da velocidade do movimento. Isto pode ser observado no seguinte exemplo simples. Quando se aquece um gás num recipiente é-lhe transmitida uma determinada energia. A velocidade do movimento calorífico caótico das moléculas depende da temperatura e aumenta com o aquecimento do gás. O aumento da velocidade do movimento das moléculas, de acordo com a fórmula (6) , significa o aumento da massa de todas as moléculas. Consequentemente, a massa do gás no recipiente aumenta quando aumenta a sua energia interna. Entre a massa do gás e a sua energia existe uma relação.
A relação entre a massa e a energia no caso de um movimento lento. É mais simples estabelecer a relação entre a massa e a energia no exemplo do movimento de um corpo com velocidade v , bastante menor do que a velocidade da luz c . Para isso, deduzamos a expressão aproximada da dependência da massa em relação à velocidade quando v << c . O denominador na fórmula ( 6) escreve-se sob a forma.
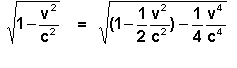
Desprezando a grandeza
obtemos:
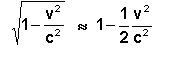
Por isso
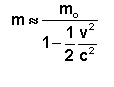
Multiplicando o numerador e o
denominador por 
e desprezando
de novo o membro
, obtemos a seguinte
fórmula aproximada:
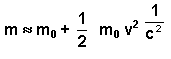
Daqui resulta que a variação
da massa do corpo
, quando aumenta
a sua energia cinética em
exprime-se assim
Isto significa que o incremento da massa do corpo quando aumenta a sua velocidade, é igual à energia cinética que lhe é transmitida, dividida pelo quadrado da velocidade da luz.
A fórmula de Einstein. Na teoria da relatividade, este resultado é amplamente generalizado. Com o auxílio desta teoria, Einstein estabeleceu a relação geral entre a energia e a massa, que é dada por uma fórmula muito simples:
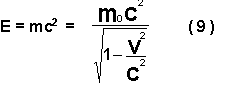
A energia dum corpo ou dum sistema de corpos é igual à massa multiplicada pelo quadrado da velocidade da luz. Em toda a física só se encontram duas ou três fórmulas universais tão simples como esta que relacionam as grandezas físicas fundamentais.
Se a energia do sistema varia, então varia também a sua massa:
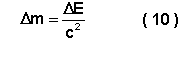
Visto que o coeficiente 
é
muito pequeno, para que se note a variação da massa é
necessário que haja grandes mudanças de energia. Quando se
dão reações químicas ou quando se aquece um
corpo em condições habituais, a variação da
energia é tão pequena que variação correspondente
da massa não pode ser verificada experimentalmente. Uma chaleira
quente tem a massa maior do que uma fria; mas nem com o auxílio
de balanças muito sensíveis seria possível medir a
diferença. Só quando se transforma o núcleo atômico
e as partículas elementares é que a variação
de energia é tão grande que a alteração da
massa nessa altura já pode ser verificada.
Quando explode uma bomba de hidrogênio liberta-se uma grande quantidade de energia - certa de 1017 J. Esta energia é superior à produção de energia elétrica em toda a Terra durante vários dias. A energia é transportada com a radiação. A radiação, além da energia, tem massa, que é aproximadamente igual a 0,1% da massa dos materiais iniciais.
Energia de repouso. Quando a velocidade do movimento de um corpo é reduzida ( v << c) , então a fórmula ( 9 ) pode escrever-se sob a forma 1 ) :
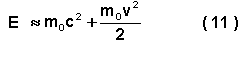
Neste caso, o segundo termo é a energia cinética habitual do corpo. Maior interesse desperta o primeiro membro : ele define a energia do corpo quando a velocidade é igual a zero ¾ a chamada energia de repouso E 0 :
Este resultado merece atenção. Qualquer corpo, pelo simples fato de existir, tem uma energia que é proporcional à massa de repouso m0 .
Quando se transformam partículas elementares com massa de repouso diferente de zero, em partículas com m0 = 0 , a energia de repouso das primeiras é transmitida às segundas totalmente sob a forma de energia cinética.
Este fato é a demonstração experimental mais evidente da existência de energia de repouso.