Limits are actually one of the easier concepts of Calculus to understand. They are of two
varieties: directional and non-directional. A non-directional limit would take the form of:
It just so happens that the answer to both of these limits have the same answer; however, be
cautioned that this will not always be the case. The first example is an absolute limit, the second
is a limit taken as the function approaches from the right (or positive) side of the point. If it had
been a - instead of a +, then it would have approached from the left (or negative) side of the point.
A simple definition for a limit is the value that a function approaches as the value of the variable
gets near the given point.
In the example above, we are asking, "What value does (x2-1)/(x-1) approach as x gets near 1.
All good Algebra I students would tell you that this value can not be determined because x-1=0!
However, with Calculus and the use of limits, we can determine what value it will approach.
WORD OF CAUTION: The value of (x2-1)/(x-1) is still undeterminable because we can NOT
divide by zero.
As to the working of this problem, there are several ways that it can be done:
Make a chart of values
If we were to put various values in for x, we would come up with the following table:
|
X |
Value |
| 1.1 | 2.1 |
| 1.01 | 2.01 |
| 1.001 | 2.001 |
| 1.0001 | 2.0001 |
| 1.00001 | 2.00001 |
| 1.000001 | 2 |
Because of the precision that my calculator was using, we got an imprecise value for the last one,
it should have been 2.000001, but we can see the trend very clearly. As x gets close to 1, the
value gets closer to 2. We can deduce from this that the limit of (x2-1)/(x-1) as x approaches 1
from the right is equal to 2.
Notice, however, that the above chart is incomplete. This is due to the fact that our chart only considers the values from the RIGHT side of 1. In order to complete the non-directional limit, we would also have to find:
|
X |
Value |
| .9 | 1.9 |
| .99 | 1.99 |
| .999 | 1.999 |
| .9999 | 1.9999 |
| .99999 | 1.99999 |
| .999999 | 1.999999 |
| .9999999 | 1.9999999 |
The values in this chart provide us with the limit from the left as being equal to two. Since the
directional limit from the left and the right are both equal to two, then the non-directional limit is
also equal to two.
As one can see, this is probably not the way that you want to do all of your limits. It is important that you consider both directions in a non-directional limit because sometimes they do not match. When this happens then it is said that the non-directional limit "does not exist."
Graph
The second method of determining limits (and probably the most unreliable one) is to graph the equation. I say that it is unreliable for many reasons.
However, if we are not looking for precision, then graphing is a method that we can use. Let us
consider the example that we have been using. If we were to graph it, we would get:
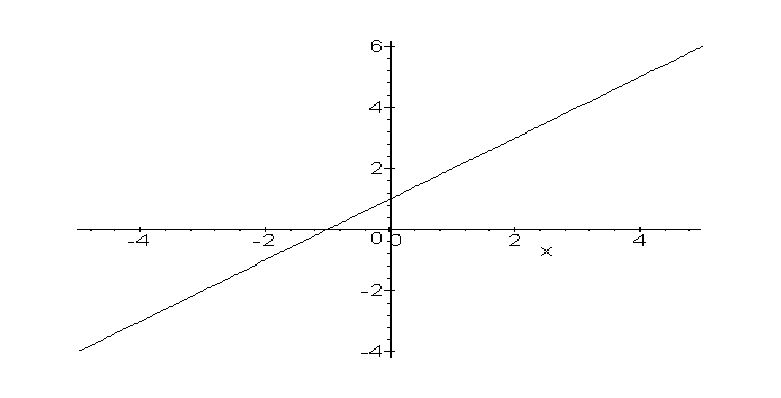
By examining this graph, one can tell that as x gets closer to 1, the value of the expression in question gets closer to 2. This happens from both the left and the right side of x=1, so all three of the limits (left, right, and non-directional) for this expression at 1 are equal to 2.
Plug it in
Of course, this is not the most technical way of saying it, but substituting the value in for x will often work. In most cases, however, there is some additional work to be done first. Most definitely in this case since the denominator is equal to 0. Consider this, though:
(x2-1)/(x-1)=(x-1)(x+1)/(x-1)=(x+1)
It is a very simple matter to now substitute a 1 in for x. At x=1, x+1=2.
Notice that we got the same limit as we did using the other two methods. It still remains, however, to determine if that is a non-directional limit or a directional one. This can easily be accomplished by sketching a quick graph or substituting values on either side of 1 as was done in the previous two methods.
Warning: If you have not studied derivatives, do not read this. The use of this method
requires knowledge of derivatives, and if you have not yet studied derivatives, then it may only
serve to confuse you. Please read the section on derivatives first and then return. (That
should take a while.)
It happens on occasion that the expression can not be simplified as was done in the last section.
When that happens, there is an alternative to tables or graphing and that alternative is L'Hôpital's
rule.
L'Hôpital's Rule: If the expression in a limit is of the form f(x)/g(x) and evaluates to 0/0 or /
at the point in question, then the limit is equal to the limit of f'(x)/g'(x) at the same point.
Simply stated, if when we plug the value in, we get 0/0 or /, then we can take the derivative of
both the numerator and the denominator and try again. If it still can not be resolved then this rule
can be used again.
Do NOT immediately use L'Hôpital's rule! The best method is still to simplify and plug in. Although I can not think of an instance where it will give an incorrect result, you should still try to simplify first. Don't take the lazy way out. For the sake of argument, however, let's consider our problem.
F(x)=x2-1 G(x)=x-1
F'(x)=2x G'(x)=1
Therefore, it becomes a simple matter of:
Plugging it in, we get, 2(1) = 2.
Consider this problem: