Cinética Química

LEYES DE VELOCIDAD PARA REACCIONES ELEMENTALES

Se ha definido la velocidad de una reacción en términos de concentraciones, órdenes y constantes de velocidad. Enseguida se considerará el comportamiento con respecto al tiempo de la concentración de los reactivos en reacciones elementales con órdenes simples. El comportamiento con respecto al tiempo se determina integrando la ley de velocidad para una expresión de velocidad particular.

REACCIONES DE ORDEN CERO

La ley de velocidad para una reacción de orden cero es (7):

Las reacciones de orden cero se encuentran más frecuentemente en reacciones heterogéneas en superficies. La velocidad de reacción en este caso es independiente de la concentración de la sustancia reactiva. Para encontrar el comportamiento con el tiempo de esta reacción, la ecuación (7) se escribe en la forma diferencial (8)

Cuando se integra (8) entre los límites t₁ y t₂, y asumiendo que la concentración de la sustancia reaccionante es [A]₀ en t₁ y para t₂ = t es [A]_t, por lo que la ecuación (8) queda:

(9)

(10)

(11)

Una gráfica de [A] contra tiempo da una línea recta cuya pendiente es k y el valor de la ordenada al origen es [A]₀.

REACCIONES DE PRIMER ORDEN.

Una reacción de primer orden es aquélla en la que la velocidad de reacción depende únicamente de un reactivo.
Por ejemplo, la isomerización de isocianuro de metilo, CH₃NC: CH₃NC => CH₃CN

Este tipo de reacciones se pueden representar como A => B; la velocidad de desaparición de A se puede escribir de la siguiente manera:

(12)
Note que la reacción es de orden 1 con respecto al reactivo A. Por lo que, ya que solamente una molécula de A desaparece para producir una molécula de producto B, a es igual a 1, y la ecuación (12) queda:

(13)

Para resolver la ecuación diferencial se separan las variables y se integra:

(14)

(15)

Si se aplican las condiciones a la frontera, de forma que para t=0 para el tiempo inicial, el valor de A es [A]0, se puede eliminar la constante de integración de la ecuación (15):

(16)

(17)

(18)

Por lo que en la ecuación (15):

(19)

La ecuación (18) se puede escribir en varias formas. Algunas de las más comunes son:

(20) Vale la pena recordar estas formas de la expresión de velocidad integrada para reacciones de primer orden. A partir de las últimas dos formas de la ecuación 20 podemos determinar una constante de tiempot, que se conoce como el tiempo de decaimiento de la reacción y se define como el tiempo requerido para que la concentración disminuya 1/e de su valor inicial [A]₀, donde e » 2.7183, la base de los logaritmos naturales. El tiempo t está dado por:

(21) Cuando se determinan las constantes de velocidad experimentalmente, la forma integrada de la ley de velocidad se escribe generalmente en logaritmos base diez

(21) una gráfica semilogarítmica de [A]_t contra t dará una línea recta cuya pendiente es k/2.303 y la ordenada al origen es [A]₀.

REACCIONES DE SEGUNDO ORDEN.

Hay dos casos de cinéticas de segundo orden. El primer caso es una reacción entre dos especies idénticas:

A + A => productos la expresión de velocidad para este caso es:

(22)

El segundo caso es una reacción global de segundo orden entre dos especies diferentes:

A + B => productos

En este caso la reacción es de primer orden con respecto a cada uno de los reactivos

(23)
Note la aparición del coeficiente estequiométrico 1/2 en la ecuación (22), pero no en la (23). Si integramos la ecuación (22), se obtiene:

(24)

(27)

Una gráfica del inverso de la concentración de A contra tiempo debe dar una línea recta de pendiente igual a 2k y ordenada al origen 1/[A]₀. Para integrar la ley de velocidad del segundo caso, es definir una variable del progreso de la reacción x, de la siguiente manera:

(28)

donde [A] ₀ y [B] ₀ son las concentraciones iniciales. La expresión de velocidad definida por la ecuación (23) se puede rescribir en términos de x de la siguiente manera:

(29)

Se integra entre límites:

(30)

Para resolver la integral del lado izquierdo de la ecuación (30) se separan las variables y se utiliza el método de las fracciones parciales:

(31)

(32)

ECUACIONES DE TERCER ORDEN.

Hay tres tipos posibles de reacciones de tercer orden:

3A => productos
2A + B => productos
A + B + C => productos

En el primer caso la ley de velocidad depende de la tercera potencia de un reactivo:

(33)

Esta ley de velocidad se puede integrar fácilmente para obtener la solución:

(34)

(35)

Una gráfica del inverso del cuadrado de la concentración de A contra t debe dar una línea recta de pendiente igual a 6k y ordenada al origen 1/[A]₀².

El segundo caso es una reacción de segundo orden con respecto a A y primer orden con respecto a B. La ley de velocidad es:

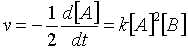(36)

Una forma fácil de integrar la ecuación (36) es cuando las concentraciones iniciales de A y B son iguales. Al integrar la ley de velocidad para este caso, es conveniente introducir una variable de progreso, en forma semejante a lo que se hizo para las reacciones de segundo orden. Se define una variable de progreso y:
y con esta condición podemos rescribir la ecuación (36) en términos de y:

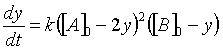(37)

Reacomodando

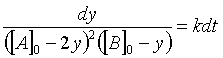(38)

Integrando por fracciones parciales

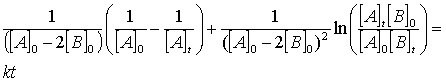(39)

El tercer caso es cuando se tiene una reacción que tiene dependencia de primer orden en cada uno de los componentes:

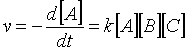(40)

La integración se lleva a cabo por fracciones parciales y se deja como tarea.

Dos ejemplos que se encuentran en la literatura de reacciones de tercer orden son, por ejemplo, el proceso de recombinación de tres cuerpos, tal como

I + I + M => I₂ + M
ó
O + O₂ + M => O₃ + M.
En estos casos el tercer cuerpo actúa para eliminar el exceso de energía de los reactivos recombinantes estabilizando los productos.

Otro ejemplo es la reacción en fase gaseosa:

2NO + O₂ => 2NO₂

REACCIONES DE CUALQUIER ORDEN.

No hay ejemplos en la literatura de reacciones de cuarto, quinto o mayor orden. El mayor orden de reacción que se ha encontrado empíricamente es tercero. Sin embargo, en forma general la expresión de velocidad es:

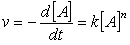(41)

Una integración simple de esta expresión da como resultado:

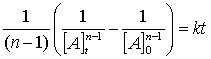(42)

que se puede rescribir como:

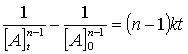(43)

La ecuación (43) es válida para cualquier valor excepto n = 1.
En la siguiente figura se muestra una gráfica de concentración contra tiempo para reacciones de diversos órdenes. *********GRAFICA DE ORDENES********* En el caso general no hay una gráfica simple que se pueda construir para probar el orden de una reacción, como puede hacerse para los casos de primer y segundo orden.

Cuando se desconoce el orden de una reacción, se puede construir una gráfica de Van’t Hoff como una ayuda para deducirlo.
En una gráfica de Van’t Hoff, se grafica el logaritmo de la velocidad en función del logaritmo de la concentración del reactivo A. Esto es equivalente a hacer una gráfica de la ecuación (43) en papel logarítmico. La pendiente de dicha gráfica nos da el orden n de reacción. Se muestran algunos ejemplos en la siguiente gráfica.

REACCIONES DE PSEUDO-ORDEN.

Suponga que una reacción es de segundo orden:

(23)

Suponga adicionalmente que la concentración de B se mantiene esencialmente constante durante el periodo de observación del experimento, por lo que la ecuación de velocidad se puede escribir:

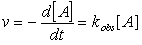(44)

en donde

k_obs=k[B](45)
En este caso se dice que la reacción de segundo orden se ha transformado en una de pseudo-primer orden. La constante k_obs es una constante de velocidad de pseudo-primer orden, a la que en ocasiones se le simboliza como k_ap (constante de velocidad aparente de primer orden). Si las concentraciones de todos los reactivos permanecen esencialmente constantes, se genera una reacción de pseudo-cero orden.
Esta capacidad de reducir el orden de reacción manteniendo una o más concentraciones constantes es una herramienta experimental muy valiosa, que permite a menudo la simplificación de la cinética de la reacción.
Es aún posible transformar una ecuación de velocidad complicada en una simple.
Existen varias formas de lograr esencialmente la constancia de la concentración del o los reactivos.
Si tomamos como ejemplo la ecuación (23) y fijamos las condiciones de forma que la concentración de B sea mucho mayor que la de A, es decir [B]>>>[A] entonces mientras la concentración de A cambia de [A]₀ a [A] = 0, [B] permanece esencialmente constante en un valor igual a [B]₀. Por ejemplo, si [B]₀ = 100 [A]₀, [B] disminuirá solamente 1% cuando la reacción haya terminado. Este cambio no es significativo para los métodos analíticos ordinarios.
Un segundo método para lograr constancia de un reactivo consiste en utilizar un sistema tampón o buffer, lo que por ejemplo puede mantener el pH constante.
Otro ejemplo es proporcionado por la reacción de disolución de primer orden de una sustancia en presencia de su fase sólida. Si la velocidad de disolución es mayor que la velocidad de reacción del soluto disuelto, la concentración del soluto permanece constante debido al equilibrio de solubilidad y la reacción de primer orden se convierte en una de pseudo-cero orden.
Si el disolvente es un reactivo, éste se encuentra en gran exceso y no se observará su participación cinética.
De esta forma, una reacción bimolecular de hidrólisis generalmente sigue una cinética de primer orden.
Peligro de trabajar bajo condiciones de pseudo-orden: alta concentración de una impureza que pueda ser reactiva y que esté contenida en el reactivo en exceso.
Determinación del orden de una reacción