 (46)
(46)
Cuando se determina el orden de reacción graficando la ecuación de velocidad integrada, se obtiene lo que a veces se nombra, orden con respecto al tiempo. Este orden no será ambiguo siempre que sea independiente del tiempo durante todo el lapso en que se efectúa la reacción.
Sin embargo, es común observar curvatura de alguna gráfica de este tipo después de las primeras dos o tres vidas medias. Una causa posible de tal desviación puede ser un cambio en las condiciones ambientales, tal como el pH, conforme procede la reacción.
Considérese el caso de una reacción de primer orden
 (46)
(46)Por definición para t = t1/2, [A]t = [A]0/2, por lo que la ecuación (46) se puede rescribir:
 (47)
(47)
 (48)
(48)Para una reacción de primer orden t1/2 es independiente de la concentración. Por otra parte, para una reacción de orden n > 1, el tiempo de vida media es:
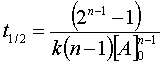 (49)
(49)
donde k es la constante de velocidad y [A]0 es la concentración inicial del reactivo.
Consecuentemente una gráfica del logaritmo de t1/2 contra el logaritmo de [A]0 debe ayudarnos a determinar el orden de la reacción.
Otra posibilidad es que se lleve a cabo una segunda reacción, se puede tratar de una reacción consecutiva en que el producto de la primera presente un cambio posterior.
Un método alterno al de Van’t Hoff, y uno de los más populares para determinar el orden de reacción es el método de vida-media.
El tiempo de vida media t1/2 de una reacción se define como el periodo de tiempo necesario para que la concentración de un reactivo específico disminuya a la mitad de su concentración inicial.
Medir t1/2 como función de la concentración inicial puede ayudar a establecer el orden con respecto a ese reactivo.
Si se toma el logaritmo de ambos lados de la ecuación (49):
 (50)
(50)
Una gráfica de esta expresión es una línea recta con pendiente igual a n-1, a partir de la cual se puede determinar el orden.
Con esta información y uno o más valores de tiempo de vida media se puede calcular la constante de velocidad.
Consideremos la ley de velocidad  (51)
(51)
Si se inicia la reacción y se mide [A] como función del tiempo durante los primeros instantes de la reacción, entonces la pendiente de la gráfica de [A] vs t para t = 0 es la velocidad inicial de la reacción, y la ecuación de velocidad para t = 0 se escribe:
 (52)
(52) (53)
(53)El error en la determinación del orden de reacción mediante este método es despreciable, siempre que el porcentaje de la reacción sea menor al 5%.
Una ventaja de este método es que se evitan complicaciones provenientes de inhibición de la formación de productos o catálisis por reacciones subsecuentes. Otra ventaja es que permite el estudio de reacciones muy lentas que no sería práctico por otros métodos.
Hemos visto que las expresiones de velocidad son a menudo funciones simples de la concentración de los reactivos con una constante de velocidad característica 1k.
Si la expresión de velocidad está formulada correctamente, la constante de velocidad debe ser realmente una constante, es decir no debe depender de las concentraciones de especies que aparezcan en la ley de velocidad, o de cualquier otra especie presente en la mezcla de reacción.
La constante de velocidad debe ser independiente del tiempo; sin embargo, depende fuertemente de la temperatura.
Este comportamiento fue descrito por Svante Arrhenius en 1889 en base a numerosas mediciones de velocidades de reacción. Arrhenius encontró que las constantes variaban como exponencialmente en función del negativo del inverso de la temperatura absoluta:
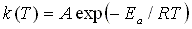 (54)
(54)La cantidad clave en la ecuación de Arrhenius es la energía de activación Ea, que puede racionalizarse como la cantidad de energía que se debe proporcionar a los reactivos para que reaccionen entre ellos. Dado que esta es una cantidad positiva, tienen k que aumentan con la temperatura.
Sin embargo, para algunas reacciones, las constantes disminuyen con la temperatura, lo que implica una energía de activación negativa. Se trata generalmente de reacciones complejas, que incluyen la formación de un intermediario que presenta enlaces débiles. Un ejemplo es la recombinación de átomos de iodo en presencia de un tercer cuerpo M:
En un diagrama de entalpía, la diferencia en energía entre los reactivos y los productos es la diferencia en sus calores de formación:
 (55)
(55)
 (56)
(56) (57)
(57)
Es claro que se requiere contar con una lectura instrumental precisa del valor final (tiempo infinito) para poder aplicar el método anterior. Sin embargo, en ocasiones no es posible medir este valor en forma precisa. En algunos casos, se puede presentar una reacción secundaria lenta, precipitación de un producto, línea base no estable del instrumento, o simple y sencillamente que la reacción sea tan lenta que no valga la pena esperar la lectura final.
Se han desarrollado métodos que permiten determinar k sin conocer la lectura al tiempo infinito, en estos procesos se estima el valor de A.
Debe aclararse que el orden de la reacción también debe conocerse. La mayor parte de los siguientes desarrollos se aplican a reacciones de primer orden.
El método más comúnmente usado para la evaluación de constantes de primer orden es el de Guggenheim. Si continuamos con el análisis espectrofotométrico como ejemplo:
 (58)
(58) (59)
(59) (60)
(60)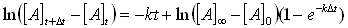 (61)
(61) (57)
(57) (62)
(62)Método de Guggenheim para la hidrólisis del Cinamato de fenilo
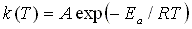 (54)
(54)| t, s | At | (t+Dt) | At+Dt | (At-At+Dt) |
| 0 | 0.837 | 400 | 0.481 | 0.356 |
| 50 | 0.763 | 450 | 0.463 | 300 |
| 100 | 0.699 | 500 | 0.477 | 0.252 |
| 150 | 0.647 | 550 | 0.431 | 0.216 |
| 200 | 0.602 | 600 | 0.421 | 0.181 |
| 250 | 0.563 | 650 | 0.411 | 0.152 |
| 300 | 0.532 | 700 | 0.402 | 0.130 |
| 350 | 0.505 | 750 | 0.397 | 0.108 |

