You may be wondering why you never notice the effects of length contraction and time dilation in everyday life. For example, if you go on vacation to some exotic location and return two or three weeks later, shouldn't you have to reset your watch when you get home? After all, according to what was mentioned about time dilation, while you are driving your watch should be running slower than the clocks in your house. Also, shouldn't the distance of the trip while you are driving be shorter than the distance indicated on the map? Well, the answer to both of the questions is . . . no. In order to notice these relativistic effects, you must be traveling close to the speed of light, which is about 186,300 miles per second (or 300 million m/s, as was mentioned earlier in the train experiment).

The effects of relativity are mathematically described by a factor most physicists indicate with the Greek letter gamma (some scientists use the letter beta, but we'll use gamma). This factor depends on the speed at which an object is moving. The gamma factor and an object's speed are directly proportional, so as speed increases, gamma increases as well. The following equations explain how this works.

Length Contraction: L_{RF =} L_P / γ

• L_RF is the length of a moving object as seen from our reference frame (contracted length)
• L_P is the length of the object as seen from its own reference frame (proper length)
• γ is the gamma factor

Time Dilation: T_{RF =} T_P * γ

• L_RF is amount of time it takes a moving object to move between two points, as measured from our reference frame (dilated time)
• L_P is amount of time it takes a moving object to move between two points (or equivalently speaking, the amount of time it takes those points to move past the object), as seen from its own reference frame (proper time)
• γ is the gamma factor

By now, you are probably wondering what equation to use to figure out what the gamma factor itself is. Well, here it is:

• V is the velocity of the object
• C is the velocity of light, which was mentioned above

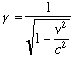
The important thing about this equation is that, for an ordinary object traveling at a reasonable speed (which is much less than the speed of light), the gamma factor will be almost exactly equal to one. The reason for this is because v²/c² will turn out to be a very small number (like 0.0000000001), so 1 minus that number will still be very close to one and the square root of the resulting number will be close to one as well. And, of course, we all know that one divided by one is one. This explains why an object must be traveling at near light speed to achieve noticeable relativistic effects.

Here are a few examples of how this works:

Example 1:

Example 2:

Of course, we all know that it is theoretically impossible for the velocity of the object to be equal to the speed of light. However, when using the gamma equation with this "impossible" situation, we obtain some very interesting results. The gamma factor itself becomes infinite. This also means that the contracted length of the object would be zero and the dilated time would be infinite. So, theoretically, an object moving at the speed of light would be invisible (because it wouldn't have any length) and it would take forever (from our point of view) to move between two points. Essentially, if an object ever attained the speed of light, from our point of view it would cease to exist! And, strangely enough, this would still obey the Law of Conservation of Mass and Energy! How, you may ask? Well, in the next section you will find out.

• Mass and Energy

• Back to Main Page