Google
 

Notations, Formulas, Terminologies and Language in Mechanics

  1. Abuses.

    1. Abuse of language and symbols, and their consequences.
      1. In [Go2, p.340, l.22], Goldstein says, "the q's are kept constant." He should have said, "the values of q=s are kept fixed" because in math "q=constant" means that q is a constant function. If q was a constant function,would be 0.
      2. Symbol abuses [Go2, p.21, (1-57); p.340, (8-2); p.342, (8-12)].

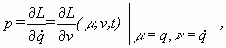
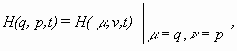
      3. How we clarify the confusion.
        (The purpose of a question vs. the timing of asking the question) In [Go2, p.364, l.-13-l.-1], Goldstein wants to argue that p and q can be varied independently. However, his argument is illogical and confusing. First, we must understand that the purpose for asking the question about independence in this case is to justify the partial differentiation MH/Mp. As mentioned in (B), the partial differentiation with respect to p consist of the following two steps: the partial differentiation with respect to v and the substitution v=p. Before the substitution, we assume u and v are independent, so we say q and p are independent, which is another example of language abuse. After the substitution, we no longer need to ask the question about whether q and p are independent because we have already finished the partial differentiation with respect to v.

    2. Choosing a right notation can prevent confusion.
          Symon needs to clarify the confusion in [Sym, p.323, l.-10] because he uses the same notation V for the two different situations [Sym, p.323, (8.142) & (8.144)]. To prevent the confusion, Chorin uses notation W in [Cho, p.9, (BM2)] and notation Wt in [Cho, p.10, (BM3)].

    3. Whenever it is possible to write out a formula neatly, do not try to describe the formula in words. Only after writing out the formula may you make comments to get a specific point across. For example, in [Go2, p.36, l.6-l.13], Golstein should have demonstrated his point as follows:

      where J is defined as in [Go2, p.37, (2-3)]. Then consider the case J'(0)=0.

    4. The audience of a textbook is the reader rather than the author. The definition of any terminology must be precise and clear. Otherwise, all the related calculations would be meaningless.
      The definitions about the concept of flux are as follows:
      1. Flux of a vector field [Cor, p.7, (1-19)].
      2. Magnetic flux density [Cor, p.326].
      3. Flux density of a beam [Go2, p.105, l.-2-l.-1].
        Once we armed with the above definitions, we can decipher the following two terms:
        1. Momentum flux density [Cor, p.602, (32-33)]:
          The total momentum of photons crossing unit area normal to the incident beam in unit time.
        2. The change in the component of the momentum flux density normal to the interface [Cor, p.603, l.12]:
          The change in the component of the momentum of (beam with a unit area cross-section [normal to the direction of propagation] and an incident angle θI) normal to the interface per unit time.

    5. In [Born, p.127, (1)], Born defines in terms of the position vector of a point on a light ray [see, Born, p.114, l.-14] and also defines as the boundary of areas [see Born, p.125, (16)]. Thus it is very confusing and troublesome that Born uses the same notation to represent entirely different concepts in the same theorem.

    6. For the computational purpose, it is convenient to identify a complex number with its real part [Hec, p.23, (2.37)]. Although the identification is valid in most cases [Yar, p.2, l.10], there are some exceptional cases that the identification will lead to mistakes. For example, Re[(a+ib)(c+id)]=ac-bd¹ac=Re(a+ib)· Re(c+id) [Yar, p.3, l.8].

    7. Confusing indices.
      1. The index in [Lan3, p.209, l.-9] or [Lan3, p210, l.-16] refers to the index number of a particle or a spinor. The index in [Lan3, p.209, l.-10] refers to the index of one component of a fixed spinor [Lan3, p.206, (56.1)].
      2. The definition of contraction [Lan3, p.209, l.14] involves one upper index and one lower index, while the antisymmetry [Lan3, p.232, l.-18] in the construction of a contraction refers two upper indices.

    8. The design of a notation should follow the grain of the topic. The relationship between r'=R-1r  and a rotation is direct [Coh, p.694, (19)], while the relationship between Dr = r'-r and a rotation is indirect. The design of the notation aR(r) in [Mer2, p.234, l.15] is based on the indirect relationship instead of the direct relationship. Therefore, it produces a meaningless equality [Mer2, p.234, l.-1] which only causes complication and confusion.

    9. A precise statement helps readers to follow the author's steps closely. In contrast, an imprecise statement frustrates readers and makes them lose their train of thought. The statement in [Mer2, p.107, l.-10] is incorrect.  The correct statement should be (k'2a®k as k'®+¥).

    10. It is better to add a few lines to clarify the meaning of a formula than to leave any notation of the formula unexplained.
       Example: [Ashc, p.274, (14.15)].
       Explanation of the notation: D(1/H).


    11. Sometimes, Landau's language is quite loose. It lacks specification and often fails to detect subtleties. The following steps may help make it more rigorous:
      1. four vector [Lan2, p.14, l.20]: contravariant vectors in the 4-dim space [Haw, p.93, (6-1)].
      2. pseudotensor [Lan2, p.17, l.20]: relative tensor of weight 1 [Haw, p.197, l.2].
      3. the equation of motion [Lan2, p.68, l.-3]: It refers to the equation of motion to be derived from [Lan2, p.69, (27.7)] rather than the equation of motion described by [Lan2, p.61, (23.4)].
      4. a tensor of third rank [Lan2, p.61, l.12]: the left-hand side of the tensor equality [Lan2, p.67, (26.5)] refers to the stage [Lan2, p.61, (23.5)] (i.e. using E and H rather than A as the starting point). The tensor on the left-hand side of the equality [Lan2, p,67, (26.5)] does not refer all the way back to the stage [Lan2, p.61, (23.3)].
        Remark. We can use [Haw, p.97, §6-8] to prove that the left-hand side of [Lan2, p.67, (26.5)] is a tensor.
      5. certain definite conditions [Lan2, p.119, l.15]: the conditions for [Lan2, p.119, (49.5)&(49.6)] to be valid are f Î L2(R) and fˆ Î L1(R) [Ru2, p.202, Theorem 9.14]. However, [Lan2, p.119, (49.8)] is valid for f Î L2(R) [Ru2, p.200, Theorem 9.13(b)].

    12. The complicated expression in [Kit2, p.642, (28)] makes it difficult to recognize the simple idea [Coh, p.489, (B-6-a)] of a creation operator.

    13. In order to prove grad R(t') = (R/t') grad t' + (R/R) [Lan, p.162, l.9], we must use the following equality:
      R(t')/x = [R(t')/x] + [R(t')/t'](t'/x), where the first partial derivative with respect to x on the left-hand side of the equality refers to all variables where x is either an explicit or a implicit parameter, while the first partial derivative with respect to x on the right-hand side of the equality refers to x that is only an explicit parameter.

    14. In quantum mechanics, we often give an abstract term a concrete name. Sometimes, the name is not only fake (due to its abstract stage) but also incorrect when it is realized in the concrete  case. For example, we  call J in [Coh, p.239, (D-17)] the probability current, but J actually refers to probability current density. However, its physical meaning cannot be realized until we apply the term to an electron placed in an electromagnetic field [Coh, p.240, (D-24)]. Even then, we must make n adjustment [Hoo, p.431, (C8)] in order to make a precise match between the two concepts (probability current and the electric current density).

    15. The use of imprecise language and nonrigorous argument makes errors undetectable.
          [Hoo, p.37, (2.7)] is derived in imprecise language and nonrigorous argument. The force in [Hoo, p.37, l.-14] should be specified to be attractive. According to the model described in [Hoo, p.36, Fig. 2.3], the correct equation of motion should be [Coh, p.558, (5)]. Furthermore, Hook fails to explain why we must choose w=0 in [Coh, p.558, (5)]. This is because there is no spring holding the n-th atom in reality [Coh, p.602, l.3-l.5]. Thus, Hook commits two mistakes during his derivation of [Hoo, p.37, (2.7)] even though his final conclusion is correct.

    16. The correlation energy [Ashc, p.336, footnote 14].

    17. An oversimplified mathematical expression requires a proper interpretation; otherwise it would be difficult to understand its meaning. However, we should also not give too much detail, because a complicated outlook may fail to preserve the expression's original form and may thereby lose the direct link for understanding. For example, the key to interpreting (A×Ñ)B is to expand each symbol into Cartesian coordinates. The left-hand side of [Cor, the front cover, Identity 14] is oversimplified, while the expansion on the right-hand side is too complicated. To avoid both disadvantages, we should adopt a middle-ground interpretation:
      (A×Ñ)B=(Ax/x+Ay/y+Az/z)(Bxx^+Byy^+Bzz^).

    18. [Wangs, p.36, (1-141)] gives the reason why u is a better notation for the gradient of u than is grad u [Kara, p.45, l.10-11]. Similarly, [Chou, p.584, l.-3] gives the reason why Ñ×u is a better notation for the divergence of u  than is div u, and [Kara, p.95, l.-3 or Chou, p.585, l.1] gives the reason why Ñ´u  is a better notation for the curl of u than is curl u.

    19. In [Zem, p.444, l.13], gn dn = the number of quantum states. In p.444, l.-6-l.-5], gn = the number of quantum states. Zemansky uses the same notation to represent two different concepts. He should have defined Gn = gn dn  first and then have replaced all the gn's in [Zem, §17-12] by Gn's.  In fact, Zemansky made two mistakes in deriving [Zem, p.446, (17-27)]. In [Zem, p.446, l.-12], he mistook gn dn  for gn; in [Zem, p.446, l.-9], he should have considered the average number of photons rather than the exact number of photons. For the correct derivation, see [Man, p.249, l.-7-p.250, l.-4]. Suppose we encounter a complicated circumstance like [Wu, p.37, l.7-l.8]. The meanings of these equalities remain clear because Wu designs his notations carefully. If we were to use Zemansky's notations instead, the situation would become unnecessarily complicated and confusing.

    20. Good ideas must be expressed with precise language.
          The meaning of the phrase "appropriate boundary conditions" given in [Chou, p.602, l.-9] is not clear. In [Chou, p.614, l.9], "Self-adjoint" is not the right word to use. In these two places, Choudhury should have specified that the required boundary conditions are those that make the right-hand side of [Bir, p.258, (8)] equal to zero.

  2. Useful notations and languages.

    1. A good notation can sometimes be used as a device to predict results before we actually prove them.
          The outlook of a series of matrix multiplications is cumbersome. Dirac's ket and bra operations [Coh, chap. II.B] reduce it to a simple expression. The trick of inserting ∑i ׀ui><ui׀ is nothing but inserting identity matrix. Dirac's notation functions amazingly well because of the associativity of matrix multiplication. For a fixed orthonormal basis ׀ui>, Dirac's device makes it easier to interpret the identity operator as ∑i ׀ui><ui׀, which serves many purposes in application. Especially, it inspires us to predict some results before we actually prove them [Coh, p.123, (C-11) & p.148, (E-15)].

    2. Hole-electron dictionary.
          Translating Chinese to English requires a Chinese-English Dictionary. Similarly, translating the language of holes to the language of electrons requires hole-electron dictionary. The content of the language of holes neither increases nor decrease that of the language of electrons. However, the language of holes is more suitable for describing the valence band, while the language of electrons is more suitable for describing the conduction band [Hoo, p.131, (5.1) & (5.2); p.139, (5.14a) & (5.14b)]. The vocabulary terms for the following concepts are key to translating the language of holes to the language of electrons:
      1. Wavevector [Kit2, p.206, (17)].
      2. Energy [Kit2, p.207, (18)].
      3. Velocity [Kit2, p.208, (19)].
      4. Mass [Kit2, p.208, (20)].
      5. The equation of motion [Kit2, p.208, (21) & (22)].
      Example. "The scattering of a hole from state k1 to k2" means "the scattering of an electron from state k2 to k1" [Hoo, p.135, l.-14-l.-13].

    3. [1].