Google
 

Exercises in Mechanics

  1. The photon gas' specific heat at constant pressure is infinite [Pat, p.191, l.−1].
    Proof.
    ∆Q=T∆S=∆E+P∆V
    =(4/3)∆E [Pat, p.191, (17)]
    >0.
    P is constant Þ T is constant [Pat, p.190, (12) & p.191, (17)]
    Þ ∆T=0.
    Cp= (dQ/dT)p=∆Q/∆T= +∞.

  2. Show that (g/V) ln (1+z) is negligible so that we are allowed to replace the summation in [Pat, p.215, (1)] with the integration in [Pat, p.215, (3)].
    Proof.
    When z is large,
    μ . εF [Pat, p.220, (36)]
    = pF2/(2m) =O(N2/3) [Pat, p.218, (23)].
    ln (1+z) = ln (1+exp(μ/kT))
    ≤ ln (1+exp(O(N2/3)/kη)) (Assume T>η)
    =O(N2/3).
    [ln (1+z)]/V= O(N−1/3) because V ~ N.

  3. (Rate of convergence)
    Supposed a function f (x) can be represented by a series. How many terms are needed to precisely approximate f (x)?
    Solution.
    Case 1. When Δk is small [Jack, p.324, Fig. 7.13], [Jack, p.324, (7.83)] converges quickly. Therefore, we only need the constant term and linear term to approximate the frequency ω(k) in [Jack, p.323, (7.80)].
    Case 2. The shape of the function f determines the building blocks of the function [Hec, p.308, l.c., l.−15-l.−9].

  4. (The hyperfine coupling between 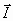and described in terms of the vector model of the hydrogen atom)
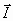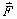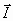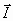        Show that in a zero-field, and precess about =+ with an angular velocity proportional to the coupling constant A between and [Coh, p.1238, l.3-l.5].
    Proof. H= þ þ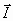 +AA .
    dIx/dt=[Ix, H]                [Lan3, p.27, l.- 12]
    =A([Ix, IxSx+IySy+IzSz])
    =A(IzSy- IySz)               [Go2, p.399, (9-75d)]
    = - A(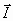´ )x
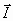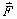    = - A(´ )x                [=-].
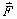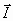    The result follows from [Kara, p.12, (1.5)].

  5. Prove [Lan5, p.11, (4.2)].
    Proof. log r = f (E,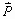,) [Lan5, p.11, l.- 21].
    Expand f in a power series of E,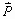 , and .
    If f (E)= b E2, then f(E+E')¹ f(E)+f(E').
    Hence f(E)= b E.

  6. Explain that the number of quantum states is the same in all inertial frames of reference [Lan5, p.36, l.- 3-l.- 1].
    Illustration. Suppose the system is described by the ring in [Rei, p.56, Fig. 2.3.1]. The squares inside the ring represent the available states of the system. When the system (the ring) moves away from the reader with constant velocity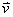 , each square’s label (position, momentum) changes, but the number of squares inside the ring remains the same.

  7. Prove [Coh, p.662, (D-5)].
    Proof. By [Lan3, p.83, (26.2); Cor, front cover, Definition 11],

    The result follows from [Sym, p.97, (3.98)].
    Remark: For a brute-force proof, see [Boh, pp.312-314] or [Lev2, pp.107-108, (5.65)-(5.67)].

  8. Prove that Rk l in [Lan3, p.122, (36.20)] is real.
    Proof. Let u = - t*.
    (The contour of integration for dt goes in the positive direction.)
    Þ (The contour of integration for dt* = - du goes in the negative direction.)
    Þ (The contour of integration for du goes in the positive direction.)

  9. Prove [Lan3, p.156, (43.9)].
    Proof 1. (x-a)-1=(x-a)[(x- a)2+d2]-1+ id [(x-a)2+d2]-1.
    I (x-a)f(x)[(x-a)2+d2]-1dx® PI f(x)(x-a)-1dx as d ® 0+.
    I d f(x)[(x-a)2+d2]-1dx®  p I f(x)d (x-a)dx as d ® 0+.
    Proof 2. Let C be the contour represented by x=a- bideiq , where b>0, q Î [- p /2, p /2].
    IC f(x)[x-(a+id)]-1dx
    ® f(a)Id[log (beiq +1)]= f(a) log [(beip /2+1)(be-ip /2+1)-1] as d ® 0+.
    log [(beip /2+1)(be-ip /2+1)-1] ® log [beip /2(be-ip /2)-1]  = p as b® +¥ .

    Remark 1. A proof shows the author's approach to the theorem. It is important to understand the author's thinking pattern. An honest and responsible author should not omit a proof [Jack, p.333, (7.117)] and should give the sources of the quoted theorem [Lan3, p.156, l.- 7, the residue] in a proof. If the quoted theorem cannot be found in a standard textbook [Complex Analysis], it is better to give a direct proof without quoting the theorem. Quoting an uncommon theorem often indicates failure to fully digest the related material.
    Remark 2. The approach of the first proof fails to estimate the contribution of the pole to the integral and fails to give a clear picture of the contour of integration. Landau’s contour approach corrects these problems. [Jack, p.333, l.- 5-p.334, l.3] fails to precisely describe the delicate limiting process that greatly facilitates the calculation of the contour integral.

  10. Explain [Mer2, p.62, (4.41)].
    Explanation.
        Divide the domain of integral into small subintervals I's so that the integration on I can be approximated by a sum.


    Example. [Schi, p.347, l.1-l.5].

  11. Dn+1(E1') and Dn+1(E2') in [Mer2, p.142, (8.29)] have opposite signs if E1'¹E2'.
    Hint. A pattern for solution will emerge once one solves the cases for n=2 and 3.

  12. Prove (a). k = k0-(½)isZ0 [Rob, p.65, l.-16]. (b). The coefficient of reflection is quadratic in s/w0 [Rob, p.65, l.-18].
    Proof. (a). [Cor, p.330, (28-61)] (let     mr=er=1). (b). Use (a) and [Cor, p.561, (30-35); p.560, (30-27), the 2nd equality].

  13. Prove s'/s =3/(2eF) [Ashc, p.257, l.-8].
    Proof. s is a function of eF [Ashc, p.255, (13.50)].
    Using [Ashc, (1.6), (2.21), (2.25)], we may explicitly express     s in terms of eF.

  14. Show that every rotation in the 4-dim space can be resolved into six rotations in the planes xy, zy, xz, tx, ty, tz [Lan2, p.10, l.3-l.4].
    Proof. [Go2, pp.146-147, (4-43)-(4-47)] & [Che, p.9, l.2].

  15. Explain [Lan2, p.20, (6-16)].
    Hint. [Cou2, vol.2, p.651, (41)].

  16. The charge distribution of an atom with closed shells is spherically symmetric [Kit2, p.66, l.2].
    Proof. [Lev2, p.327, Table 2].

  17. Prove s(q) = e0(¶F/r)| r=b [Jack, p.124, (3.137)(i)].
    Proof.

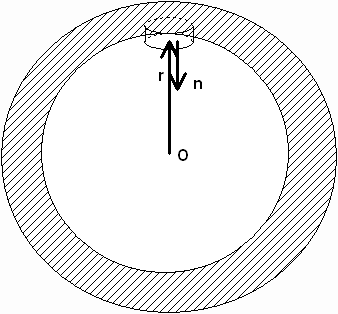
    s = q/A = (e0 òS E×nda)/A = (e0 A)E×(-r^)/A = e0(¶F/r).

  18. Why does Jtot [Wangs, p.354, l.-10] look different than J in [Cor, p.676, l.7]? Is there any inconsistency between [Wangs, p.354, (21-33)] and [Cor, p.676, (37-1)(ii)]?
    Solution. By [Cor, p.679, l.1-l.8], we obtain [Cor, p.679, (37-25)].
    Using [Jack, 6.4], we derive [Cor, p.681, (37-33)].
    When J is independent of time, [Cor, p.681, (37-33)] reduces to [Cor, p.676, (37-1)(ii)].

  19. Prove that only m=1 enters [Jack, p.205, l.1].
    Proof. Fix z>0. r®+¥ Þ  F(r,f,z)= -H0 r sin f [Jack, p.204, l.22].
    Apply this condition at the far boundary to [Jack, p.118, (3.106)]. Then we obtain
    m¹1Þ (Am(k)=Bm(k)=0 and B1(k)=0)
    by using an argument similar to the argument from [Wangs, p.193, (11-109)] to [Wangs, p.193, (11-111)].

  20. Prove [Jack, p.186, (5.56)].
    Proof. [Chou, p.207, l.-2-p.208, l.3].

  21. Prove [Jack, p.182, (5.37)].
    Hint. [Chou, p.196, (5.14) & (5.15)].

  22. Prove ò d3x r(x) eik×x = ò d3x r(x) áeik×xñl=0 part  [Jack, p.258, l.3].
    Proof. Fix r = |x|. Let x^ = x/r.
    eik×x = Sl Sm clm(r) Ylm(x^), where clm(r) = ò dW Ylm*(x^) eik×x [Coh, p.684, (46)].
    ò d3x r(x) eik×x = ò dr r2 r(r) ò dW eik×x
    = ò dr r2 r(r) 4p c00(r) Y00(x^)  (By [Coh, p.684, (45)], ò dW Ylm(x^) = 0])
    = ò d3x r(x) c00(r) Y00(x^).
    Remark. The l in [Jack, p.145, (4.1)] is the dummy index for the multipole expansion, while l in [Coh, p.684, (46)] is the dummy index for the series expansion using Ylm(x^) as the basis. Although the two indices do refer to the same basis, it would be best to treat them differently [Jack, p.146, (4.10)] in this exercise in order to avoid unnecessary confusion and distraction.

  23. Suppose a wave is incident on an interface from a medium with a lower optical density. Prove
    (a). The phase of parallel component Eúç changes only for incidence angles smaller than the Brewster angle qB [Matv, p.134, l.-18].
    (b). For angles of incidence exceeding qB, the phase of the magnetic field strength changes by p [Matv, p.134, l.-15-l.-14].
    Proof. (a). [Matv, p.132, Fig. 66] is drawn based on [Matv, (16.43)]. However, in the case of normal incidence, according to [Matv, p.129, Fig. 65], Erefl/Ein is negative. This is inconsistent with [Matv, p.132, Fig. 66] which shows that Erefl/Ein is postive.. Therefore, in reality [Matv, p.132, Fig. 66] should be corrected and appear as [Cor, p.564, Fig.30-6].
    (b). By [Cor, p.564, Fig.30-6], the phase of the parallel component Ereflúç  remains unchanged. Then we consider the normal incidence and use [Matv, p.30, (2.54)].

  24. Prove [Fur, p.203, (4.4b)].
    Proof. B = (me)1/2 E (by [Fur, (2.33) & (2.35)]).
    B×H = m-1 B×B = m-1 (me)E2 = e E2.
    Remark. Both [Jack, p.259, (6.106)] and [Wangs, p.357, (21-57)] stop at u = (1/2) e E2 + (2m)-1 B2 and move no further. They should, for doing so yields the formula given in [Fur, p.203, (4.4b)], which is important in optics.

  25. Prove [Born, p.85, (3)].
    Proof. [Born, p.77, (15)].

  26. In both [Born, p.101, (12)] and [Born, p.102, (21)], A(d) splits into two parts U and V: U represents a wave propagated with velocity c/n; V represents a wave propagated with velocity c. Prove that the U in [Born, p.101, (12)] is equal to the U in [Born, p.102, (21)].
    Proof. Any finite subset of {(r+at)n, (r+bt)m | a¹b; n, m = 0, 1, 2, 3, …} is linearly independent.

  27. (a). Prove [Jack, p.61, (2.9); p.62, (2.11)].
    (b). Prove y » a(1+2-1(q/Q)1/2) [Jack, p.61, l.-12].
    (b'). Prove y » a(1+2-1(q/(4pe0Va))1/2) [Jack, p.62, l.-5].
    Proof. (a). By [Jack, p.60, (2.6)], we have F = (4pe0)-1q(Q-q')/y2 - (4pe0)-1(q2/a2)(a/y)3[1-(a2/y2)]-2.
    Replacing Q-q' with 4pe0Va, we have [Jack,p.62, (2.11)].
    (b). Qy(y2-a2)2 = qa3(2y2-a2)
    Þ (y/a)[(y/a)2 - 1]2 = (q/Q)[2(y/a)2 - 1].
    Let y/a = 1+e. We have 4e2-2(q/Q)e-(q/Q) » 0.
    (b'). Replacing Q-q' with 4pe0Va in [Jack, p.61, (2.8)], we have [Jack, p.62, (2.10)].
    Consequently, replacing Q with 4pe0Va in (b), we have (b').


  28. Prove [Jack, p.106, (3.44)].
    Proof. Pn(cos b) is an entire function in n [Wat1, p.307, l.7-l.8]. Consequently, the zeros of this function are countable [Ru2, p.225, l.15].
    Remark 1. [Wat1, p.312, l.9].
    Remark 2. The derivation given in [Jack, p.105, l.-7-p.106, l.5] is vague and complicated.


  29. [Mari, p.206, Problem 5-18]

  30. [Mari, p.206, Problem 5-19]
    Hint. (Tearth)-1 cycles = the speed of Earth's self-revolution.
    (Tmoon)-1 cycles = the speed that the Moon obits Earth.
    [(Tearth)-1 - (Tmoon)-1] cycles = the relative rotating speed of Earth with respect to the Moon.
    The problem asks how long it takes for the relative speed to catch up half a cycle.


  31. [Wangs, pp.200-201, Exercise 11-24]


  32. Prove C1'=C3'=C5'=k1C2'+k2C4'+k3C6'=0 [Wangs, p.446, l.10].