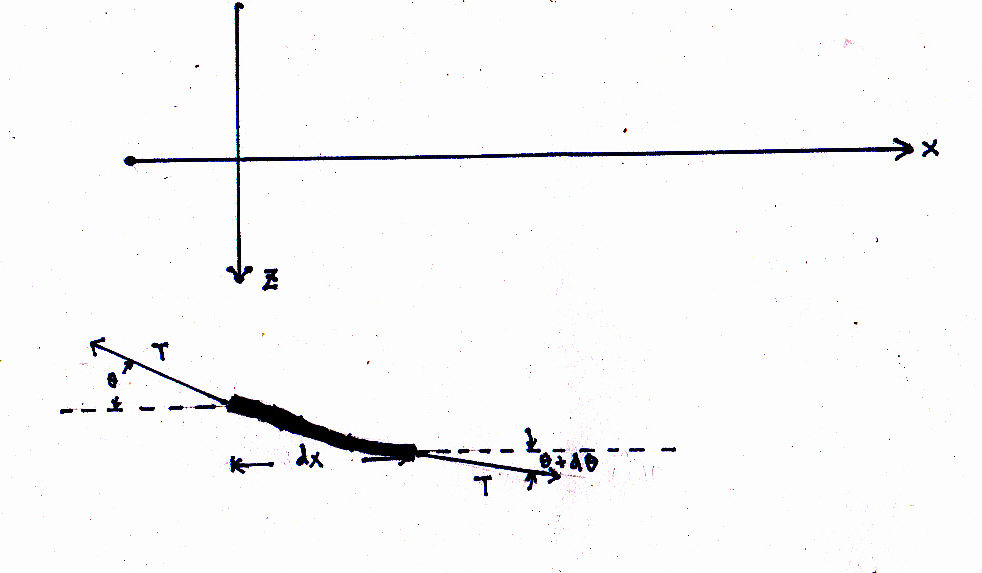
Lagrange multipliers.
Although the geometric proof of the theorem
in [Kap, p.160, l.11-l.17] is elegant and picturesque, it fails to point out its
main usage. In contrast, the algebraic proof in [Rei, pp.620-622,
§A.10] enables us to treat [Rei, p.621, (a.10.5)] as if all differentials dxk were mutually independent.
Thus it shows that the method of Lagrange multipliers makes the original problem
easy to handle. [1]
- From the viewpoint of wavefront and phase velocity [Hec, p.101, (4.4)].
- Form the viewpoint of the boundary condition [Sad, p.452, (10.98)].
Remark. Jackson's argument to prove [Jack, p.304, (7.34)] is clear [Jack,p.304, l.7-l.9], while Born's argument to prove [Born, p.37, (1)] is not.
Explaining physics should not be like playing charades. The emphasis must be clear and the explanation must be right to the point.
Good illustration: [Lan1, p.32,l.−20-p.33,l.5 & p.33, Fig.9].
Poor illustrations: [Sym, p.127, Fig. 3.34] & [Go2, pp.90-94, §3-6].
-
Reading a bad science book makes one feel as though one is falling into a bottomless swamp,
becoming trapped deeper and deeper and eventually getting buried in mud. Reading a bad science book is
similar to building a house on a shaky foundation (Wrong definition: [Sym, p.493, l.−5]; correct definition: [Haw,
§6-2 & §6-11]). No matter how far you may proceed, you must start all over. In
contrast, a good book provides easy access to subtlety, insight and depth.
Besides the definition of tensor, we need to provide efficient tests [Haw, p.99, §6-11] and counterexamples [Haw, p.196, l.−2] for absolute tensors. Abstraction or generalization can easily make these subtleties hard to recognize or obscure their motives. [Lan2, p.17, l.16-l.20] gives a partial reason why e ilkm is not a tensor, while [Haw, p.196, l.−2] tells the whole story.
The insight (The origin of [Haw, p.16, (1-21) &(1-22)]: [Haw, p.15, Fig. 1−12 & p.88, Fig. 5-10]) or key point usually comes from the author's experiences in application. Without understanding the insights, an elegant theory can be reduced to meaningless manipulating of definitions.
Depth: [Haw, pp.201-204, §13-7] provides proofs for the equations in [Lan2, p.18, l.−6-l.−1].
Example. Expressing the Maxwell equations [Wangs, p.354, (21-30)-(21-33)] in the tensor forms so that the equations are covariant with the Lorentz transformations: [Wangs, p.520, (29-134)-(29-136)].
Remark 1. [Lud, p.54, l.15; l.-9] justify the rules of lowering and raising indices, while [Lan2, l.16, l.5-l.6] and [Haw, p.125, 8-3] fail to provide such justifications.
Remark 2. [Lud, p.55, (6.8)] motivates us to define the dual of an antisymmetric tensor (see [Lud, p.55, (6.9)]), while Landau fails to provide a motive before he defines the dual [Lan2, p.17, l.30]. Landau's definition of dual emphasizes the concept "mutual", so the dual of a dual is the original. In contrast, Ludvinsen's definition emphasizes the repeat use of the same rule. Therefore, his dual of a dual is the negative of the original [Lud, p.55, (6.11)]. The above two seemingly contradictory results do not conflict.
Remark 3. [Lan2, p.17, (6.8)] defines e0123= +1, while [Lud, p.55, l.-7] defines e0123= -1. Landau's definition is just a stipulation, while Ludvigsen's definition is based on [Lud, p.36, (4.25) & (4.28)]. I prefer Ludvigsen's definition because it is consistent with the use of the Levi-Cevita tensor.
Remark 4. The reason why a parameter function l in [Lud, p.63, l.9] is characterized by the condition vaÑal=1 can be found in [O'N, p.19, Lemma 4.6].
Remark 5. [Ken, chap. 5] emphasizes the origin of tensors. Tensors are developed as a way to allow physical laws to retain their form under general coordinate transformation [Ken, p.46, l.7-l.9]. Incidentally, [Ken, p.51, l.-5] explains why the vector and covector components are the same in rectangular Cartesian coordinates.
Remark 6. Both [Pee, p.237, (8.47)] and [Haw, p.162, (11-3)] fail to provide the physical meaning of the covariant derivative, while [Ken, p.58, l.16 & p.59, Fig. 6.2] show that the key to understand the physical meaning of [Ken, p.60, (6.2)] is to use the concept of parallel transport [Ken, p.59, l.9].
Remark 7. Preserving the tensor notation [Ashc, p.445, l.-8; p.446, (22.83)] helps us trace the source of symmetry more easily (Compare [Ashc, p.445, l.8] with [Kit2, p.85, l.4]).
Remark 8. The group properties of the tensor component transformations make it possible to formulate a precise and formal definition of a tensor [Rin, pp.155-156, §A7].
Remark 9. [Jack, p.270, l.9-l.15] gives a clearer definition about polar or axial vectors than [Lan2, p.18, l.9-l.12]. [Lan2, p.18, (6.10)] shows how a cross product can be expressed as a traceless antisymmetric second-rank tensor [Jack, p.269, l.-13-l.-12].
Remark 10. [Reic, p.542] decomposes a tensor of rank 2 into three orthogonal components using dyads [Sym, p.43].
Remark 11. (Covariant differentiation of tensors of any order [Lau, pp.100-102, §9.5])
A theory requires a general solution to the problem rather than just a list of a few examples. [Kre, p.221, (74.5)] provides a general solution to the problem that [Kre, pp.220-221, §74] discusses. All the problems of the same type can be solved using this general solution. Furthermore, the method used in the general case is consistent with that used in any special case. Thus, the unification of the methods for special cases is realized. In contrast, [Pee, p.235, l.-9-p.237. l.15] fails to provide such a conclusive general solution. Although the approach in [Lau, pp.100-102, 9.5] is more methodical than that in [Pee, p.235, l.-9-p.237. l.15], it is not as simple and organized as the approach in [Kre, pp.220-221, §74].
Remark 12. (The geometric meaning of the Christoffel symbols)
[Lau, p.118, Theorem 11.2.1] provides the geometric meaning of the Christoffel symbols. In contrast, the use of [Pee, p.237, (8.53) & (8.54)] to characterize the Christoffel symbols [Pee. p.237, l.-14-p.238, l.13] fails to provide the symbol's geometric meaning.
Remark 13. Spivak's approach: a C¥ manifold M [Spi, vol. 1, p.38, l.11] ® the tangent bundle TM [Spi, vol. 1, p.91, l.4-p.93, l.6; p.101, Theorem 1] ® a section of T*M is called a covariant vector field [Spi, vol. 1, p.156, l.10] ® a covariant tensor field A of order k [Spi, vol. 1, p.160, l.-3]. Spivak's approach is cumbersome, but it has advantages. First, it specifies the base space, a manifold, and thereby justifies the nomenclature "tensor fields". In contrast, in [Kre, p.102, Definition 30.1], it is unclear whether P refers to a point in a surface or a point in the entire space. One is not sure what manifold P belongs. Second, in differential geometry the stipulation given in [Kre, p.102, (30.1)] can be proved as a theorem [Spi, vol. 1, p.158, l.4]. Third, it is nice to point out that the tensor field of the type (11) defined by dij is the evaluation map [Spi, vol. 1, p.171, l.1]. Even though Spivak tries to catch everything by building huge machinery, he still leaves out several important perspectives. There is nothing large enough to include everything. We learn a similar lesson from set theory: there exists no set of which every object is an element [Bou, p.72, l.15-l.16]. Now we discuss the disadvantages of Spivak's approach. First, his allowable transformation group is not as flexible as that in [Kre, p.102, Definition 30.1]. For example, in special relativity we must specify the allowable transformation group as the group of general Lorentz transformations [Rin, p.15, l.-7]. Second, his tensor fields are generated by dxi and ¶/¶xj [Spi, vol. 1, p.169, l.1]. Conceptually, this definition of tensor fields is too restrictive because the concept of tensors can apply to not only geometrical quantities but also physical quantities such as electric fields. In this sense, the rules given in [Kre, p.102, (30.1a) & (30.1b)] are more flexible. We must realize that the theory of tensors strides across fields of study and is applicable everywhere. Any attempt to contain it in a single field of study is simply impossible.
Remark 14. The inner product on a vector space V can be expressed in the tensor form gij [Spi, vol. 1, p.409, l.-7], while the inner product on V* can be expressed in the tensor form gij [Spi, vol. 1, p.416, l.1-l.2]. {1} The scalar product of 4-vectors is invariant under Lorentz transformations [Lan2, p.14, l.16-l.17]. The 4-vectors can be expressed in contravariant or covariant coordinates [Lan2, p.14, l.-3]. {2} Covariant coordinates are associated with reciprocal base vectors [Haw, §1-6; p.14, (1-18)]. Reciprocal base vectors form the dual basis [Haw, p.11, l.-5-l.-3]. When we talk about contravariant tensors, our setting refers to V. When we talk about covariant tensors, our setting refers to V*. Thus, the dual basis plays an important role in the theory of tensors. I wonder why most textbooks in linear algebra fail to provide the geometric meaning of the dual basis [Haw, p.15, Fig. 1-12].
- Links {1, 2, 3}.
Each section of [Fomi] is summarized into theorem form. The hypothesis and conclusion of each theorem have been clearly specified so that one can easily apply the theorem to other readings.
In [Lan1], the material has been condensed and the main results of various topics have been systematically organized so that
- we may easily see the big picture and
- we may easily move to the front line of research.
In contrast, [Go2] is more like a CliffsNotes version of [Lan1] except that it is not documented. The regurgitation in the notes style makes it difficult for the reader to understand what is going on if he is not guided by [Lan1]. Although each topic in [Go2] is discussed in great detail, the links among topics are weak. Furthermore, both [Go2]'s structure and reasoning are loose. For example, the meaning of a definition is not always precise and the assumptions of a theorem are sometimes difficult to trace. Thus extracting desired information from [Go2] is often like searching for an auto part in a junkyard. Let me give some examples to illustrate my points.
- [Fomi, p.58, l.-15] defines the canonical variables in the general sense, while [Go2, p.340, l.17] defines the canonical variables in a very narrow sense. The origin of the quantization of energy can be traced to the boundary conditions of the solution of the Schrödinger equation. Thus, the canonical variables in the general sense play an important role in quantization.
- [Fomi, p.72] gives a geometric meaning of the Legendre transformation and shows that the transformation is involutionary, while [Go2] does not.
- [Fomi, p.71, l.5] indicates that ¶Φ/¶x =[Φ,H] is valid on the integral curve of the system [Fomi, p.70, (11)]. In contrast, the failure to indicate where [Go2, p.405, (9-94)] is valid makes the calculations in [Go2, p.405, l.-10] meaningless.
- [Fomi, p.76, l.16] relates the generating function to variational problems, while [Go2, p.382, l.11] does not.
- The origin of 4-vectors [Rob, p.81].
- The definition of 4-vectors [Rob, pp.82-83, #7.1].
- The typical method of generalizing a classical physical concept to the relativistic one [Rob, pp.83-85, #7.2].
- Vector product vs. antisymmetric tensor [Rob, pp.86-88, #7.3 & pp.88-89, #7.5].
- Precession [Lan1, p.106, l.-8-p.107, l.-8; p.116, l.1-l.15].
Remark. In [Lan1, p.112, Fig. 48], let Z-axis rotate about x3-axis with angular velocity w . If we are fixed in the rotating (X,Y,Z)-frame, we will see that x3-axis rotates about Z-axis with angular velocity - w. - Nutation: [Sym, pp.454-460,
§11.5].
In [Sym, p.457, l.-15], Symon should have pointed out that we can let 1-axis coincide with Ox in [Sym, p.455, Fig.11.5] (see [Lan1, p.111, l.19-l.21]).
- Landau introduces the action integral first. After he finds the
Langrangian, he turns the crank of formalism to obtain momentum [Lan2, p.25, l.-13] and energy [Lan2, p.26, l.3].
Remark 1. [Lan2, p.24, l.-22] says that the action is invariant under Lorentz's transformations. Landau should have said that he considers time-space as a 4-vector and the Lorentz transformation as a metric tensor [Go2, p.288, (7-40) & Lan2, p.16, l.-3]. The Lagrangian is the unique entity that characterizes the equation of motion. Although its expression changes with the coordinates we choose, its value is fixed at the specific location and time.
Remark 2. Certainly, formalism lacks motivation. Even Landau's introduction of Lagrangian lacks concrete motivation because the Lagrangian itself is abstract and the concept of tensor is very complicated. Most likely, one derives [Lan2, p.25, (8.2)] only after special relativity is established.
- In contrast, [Eis, pp.A-13-A-17] pays attention to the impact of special relativity to each individual concept in classical mechanics. Thus Eisberg generates more interfaces of special relativity with classical mechanics [1] and creates the motivation behind new concepts. For example, to preserve the conservation law for momentum, we must allow the mass of a particle to change with its speed [Eis, p.A-14, l.- 8]. Furthermore, the direct interface of special relativity with a concept in classical mechanics rather than the indirect interface with formalism greatly helps us visualize the new concept in special relativity.
- Both the example in [Rob, p.55, l.-16-l.-14] and the example in [Eis, p.A-13, Fig. A-7] lead to the same result [Rob, p.56, (5.7) & Eis, p.A-14, (A-18)]. We prefer to use the former example because it is simpler than the latter example.
- [Rob, p.57, l.-2-p.58, l.2] indicates that if the total momentum and mass of a system of particles were conserved in one inertial frame, then they would also be conserved in another initial frame, while [Eis, pp.A-13-A-15] does not.
[Sym, p.395, l.7-p.396, l.8] details important similarities between the movement of the phase "particles" and that of particles in an incompressible fluid. [Rei, pp.626-628] gives an excellent analytic proof of Liouville’s theorem. [Go2, p.427, Fig. 9-3] provides a vivid geometric interpretation; [Go2, p.428, l.1-l.5] gives the intuitive physical meaning of Liouville’s theorem [1]. It is easier to explain [Rei, p.54, l.18-l.22] by using [Go2, p.428, l.1-l.5] than using [Rei, Appendix A.13]. The way that Landau defines a statistical ensemble in [Lan5, p.9, l.!2-l.!1] immediately shows that [time average] = [ensemble average].
Remark 1. [Ashc, p.771, Appendix H] extends Liouville's theorem to semiclassical motion.
Remark 2. [Pat, p.35, (5)] can be explained more intuitively and rigorously using [Kara, p.152]. Pathria's 3-dim proof [Pat, §2.2] of Liouville's theorem is a natural approach to the problem, while Reif's 1-dim proof [Rei, Appendix A.13] is more fundamental in logic.
- noninteracting = there are no cross-terms in the expression of Hamiltonian. The normal mode is the device to reduce the complicated problem of N interacting atoms to the equivalent problem of 3N noninteracting harmonic oscillators [Rei, p.408, l.22-l.24].
- Phonons are indistinguishable [Rei, p.409, l.- 11].
- Phonons obey Bose-Einstein statistics [Rei, p.409, l.-16] not because there is infinite number of them (The reason that Reif gives in [Rei, p.338, l.3-l.4] is incorrect) but because a quantum number nr is a state index which is allowed to range from 1 to +¥ without any restrictions [Eis, p.401, l.1-l.2].
- The quantum state of the whole system is specified by the set of 3N
quantum numbers {n1, n2, …, n3N}[Rei, p.408, l.-6]. Each phonon can be in any one of the 3N states with energies
ħwr (r
=1,…, 3N) [Rei, p.409, l.15]. Therefore, from the
viewpoint of quasi-particles, the state of the system = (n1 phonons
in state 1, …, n3N phonons in state 3N). From the viewpoint of
standing wave, see [Eis, p.389, l.14].
Remark. According to [Coh, p.602, l.7-l.10], a phonon is actually characterized by a wave vector and an angular frequency W(k). The discussion about phonons in [Rei, pp.407-411, §10.1] is restricted to the condition [Coh, p.603, (82)]. - The speed of sound (acoustical waves): [Hoo, p.35, (2.3)](when atomic spacing << atom displacement << wavelength [Hoo, p.35, l.-12-l.-11]); [Hoo, p.40, (2.13); Coh, p.603, (84)](chain of identical atoms); [Hoo, p.44, l.-11](chain of two types of atoms).
- Lattice vibrations of 3-dimensional crystals: [Hoo, p.46, l.-12-l.-8].
Good illustration: [Lan5, pp.65-68, §22].
Poor illustration: [Rei, p.298, l.- 8-p.300, l.10].
- [Boh, pp.321-326,
§14.14 & §14.15].
The quality of a textbook on quantum mechanics can be determined by noting whether or not it includes a complete analysis of the Legendre polynomials. - Merits in [Col].
- Spherical harmonics Yn come from a solution of Laplace's equation that is a homogeneous polynomial of degree n [Col, chap.IV, '1.1].
- Surface harmonics in Cartesian coordinates and spherical coordinates. Their sign regions. [Col, p.232].
- Notice the 1-1 correspondence between [Col, p.232, Fig.IV.2, n=2] and [Coh, p.682, (33)].
- For the geometric origin of the generating function, the explanation in [Col, p.233, l.!4-p.234, l.!7] is much better than that in [Cou, p.85, l.11-l.18].
Quantization.
- Experimental evidence: discrete values for physical quantities [Schi, p.2, l.-3; p.3, Table 1].
- Theoretical evidence:
- Responding to the above experimental evidence, we study the corresponding eigenvalues of operators.
- Quantization stems from the formalism of classical mechanics.
- [Schi, p.132, (23.2)] and [Schi, p.134, (23.8)] allow us to establish the correspondence [Schi, p.134, (23.9)].
- A Poisson bracket does not depend on the canonical variables we choose [Lan1, p.145, (45.9)]. A commutator
bracket does not depend on the basis we choose.
- Quantization rules [Schi, p.135, l.15-l.29].
Example: second quantization [Schi, p.342, l.12; p.349, (46.3); p.350, l.1 & (46.6)].
Remark 1. Summerfeld's quantization of action implies both Planck's quantization of energy and Bohr's quantization of angular momentum
[Eis, p.110, l.-5-p.112, l.-7].
The quantization of action can be interpreted in terms of standing waves [Eis,
p.112, l.-6-p.114, l.19]. Schrödinger derives energy quantization
based on the fact that accepted solutions of the time-independent Schrödinger
equation exist only for certain value of the total energy ([Coh, pp.351-358,
Complement MIII]Ú[Eis, p.160, l.-15-p.163,
l.-15]Ú[Lan3, p.61, l.1-p.62, l.8]Ú[Mer2,
p.45, l.8-l.20]). Thus, Schrödinger
eliminates the axiomatic requirement of integralness, and traces its
origin directly to the boundary conditions of an eigenfunction ([Eis, p.163, l.-8-l.-5]
& [Lev2, p.69, (4.47); p.70, l.9; p.70, Fig. 4.2]).
Remark 2. In [Eis, p.163, l.-6], Schrödinger
attributes integralness to the finite and single-valued nature [Lev2, p.109,
l.1] of an eigenfunction. According to the theory of differential equations,
it is more appropriate to attribute the discreteness of eigenvalues to boundary
conditions [Chou, p.136, l.-18-p.137, l.4; Bir, pp.288-292].
However, it is important to point out that the discrete spectrum of the
regular S-L system [Bir, p.273, Theorem 5] inspires Schrödinger to
interpret the discreteness in the microscopic world using Schrödinger
equation. At the point when readers encounter [Eis, p.163, l.-6],
Eisberg has not yet provided enough mathematical background for them to appreciate Schrödinger's
statement. However, most textbooks that do build sufficient background forget to mention
that this
clue led to the important discovery. Thus, many textbooks often fail to
accurately reflect history when they explain the theory (see [Bir, chap.10,
§16; Jack, p.77, l.7; Coh, p.663, l.-14]). - The Poisson algebra and the commutator algebra are isomorphic Lie algebras.
Proof. The generators of the two algebras produce the same results (Compare [Schi, p.134, (23.10)] with [Coh, p.222, (B-33)].
The rules of Poisson brackets and those of commutator brackets are the same [Schi, p.135, (23.12); Coh, p.168, (10)-(14)].
- Through the canonical transformation
in [Fomi, p.93, l.14], we see that the canonical equations of motion and the
Hamilton-Jacobi equation are equivalent [Fomi, pp.88-93,
§23]. Therefore, we may express the general equation of motion in the form of the
Hamilton-Jacobi equation. Finally, we use quantization rules to establish the time-dependent Schrödinger
equation from the Hamilton-Jacobi equation.
Indeed, in the quasi-classical case [Lan3, p.20, (6.1)], the time-dependent Schrödinger
equation reduces to the Hamilton-Jacobi equation of classical mechanics [Mer2,
p.23, (2.39)].
Remark. The ultimate goal of quantization is to derive the Schrödinger
equation. Consequently, the correspondence principle should be formulated in its
strongest form. The correspondence between classical mechanics and quantum mechanics established by [Mer2, p.326, (14.61) & (14.62)] is a
weak form of the correspondence principle because Merzbacher's
formulation cannot
lead to the derivation of the Schrödinger equation. Indeed,
Schrödinger's equation implies [Mer2, p.326,
(14.62)], see [Coh, p.241, l.1-l.9]; Hamilton's equations implies [Mer2, p.326,
(14.61)], see [Lan1, p.135, l.6-l.11].
- The beauty of commutator algebra is that we jettison the complicated
calculation required with Poisson brackets and preserve its algebraic essence. The
reduction greatly simplifies qualitative discussion of physical phenomena.
Furthermore, we may apply the commutator algebra and the Schrödinger
equation to a microscopic system.
- How to use the concept of wave packets to connect classical and quantum mechanics.
- A wave packet is the wave function of a localized particle [Coh, p.26, l.-11-l.-9].
- The group velocity of the wave packet = the velocity of the (free) particle
[Coh, p.29, (C-28)].
- The correspondence principle: the classical value of a physical quantity =
the expectation value of the corresponding operator [Schi, p.26, (7.9);
p.27, (7.10)].
- Responding to the above experimental evidence, we study the corresponding eigenvalues of operators.
- Quantization stems from the formalism of classical mechanics.
- [Schi, p.132, (23.2)] and [Schi, p.134, (23.8)] allow us to establish the correspondence [Schi, p.134, (23.9)].
- A Poisson bracket does not depend on the canonical variables we choose [Lan1, p.145, (45.9)]. A commutator bracket does not depend on the basis we choose.
- Quantization rules [Schi, p.135, l.15-l.29].
Example: second quantization [Schi, p.342, l.12; p.349, (46.3); p.350, l.1 & (46.6)].
Remark 1. Summerfeld's quantization of action implies both Planck's quantization of energy and Bohr's quantization of angular momentum [Eis, p.110, l.-5-p.112, l.-7]. The quantization of action can be interpreted in terms of standing waves [Eis, p.112, l.-6-p.114, l.19]. Schrödinger derives energy quantization based on the fact that accepted solutions of the time-independent Schrödinger equation exist only for certain value of the total energy ([Coh, pp.351-358, Complement MIII]Ú[Eis, p.160, l.-15-p.163, l.-15]Ú[Lan3, p.61, l.1-p.62, l.8]Ú[Mer2, p.45, l.8-l.20]). Thus, Schrödinger eliminates the axiomatic requirement of integralness, and traces its origin directly to the boundary conditions of an eigenfunction ([Eis, p.163, l.-8-l.-5] & [Lev2, p.69, (4.47); p.70, l.9; p.70, Fig. 4.2]).
Remark 2. In [Eis, p.163, l.-6], Schrödinger attributes integralness to the finite and single-valued nature [Lev2, p.109, l.1] of an eigenfunction. According to the theory of differential equations, it is more appropriate to attribute the discreteness of eigenvalues to boundary conditions [Chou, p.136, l.-18-p.137, l.4; Bir, pp.288-292]. However, it is important to point out that the discrete spectrum of the regular S-L system [Bir, p.273, Theorem 5] inspires Schrödinger to interpret the discreteness in the microscopic world using Schrödinger equation. At the point when readers encounter [Eis, p.163, l.-6], Eisberg has not yet provided enough mathematical background for them to appreciate Schrödinger's statement. However, most textbooks that do build sufficient background forget to mention that this clue led to the important discovery. Thus, many textbooks often fail to accurately reflect history when they explain the theory (see [Bir, chap.10, §16; Jack, p.77, l.7; Coh, p.663, l.-14]). - The Poisson algebra and the commutator algebra are isomorphic Lie algebras.
Proof. The generators of the two algebras produce the same results (Compare [Schi, p.134, (23.10)] with [Coh, p.222, (B-33)]. The rules of Poisson brackets and those of commutator brackets are the same [Schi, p.135, (23.12); Coh, p.168, (10)-(14)]. - Through the canonical transformation
in [Fomi, p.93, l.14], we see that the canonical equations of motion and the
Hamilton-Jacobi equation are equivalent [Fomi, pp.88-93,
§23]. Therefore, we may express the general equation of motion in the form of the
Hamilton-Jacobi equation. Finally, we use quantization rules to establish the time-dependent Schrödinger
equation from the Hamilton-Jacobi equation.
Indeed, in the quasi-classical case [Lan3, p.20, (6.1)], the time-dependent Schrödinger equation reduces to the Hamilton-Jacobi equation of classical mechanics [Mer2, p.23, (2.39)].
Remark. The ultimate goal of quantization is to derive the Schrödinger equation. Consequently, the correspondence principle should be formulated in its strongest form. The correspondence between classical mechanics and quantum mechanics established by [Mer2, p.326, (14.61) & (14.62)] is a weak form of the correspondence principle because Merzbacher's formulation cannot lead to the derivation of the Schrödinger equation. Indeed, Schrödinger's equation implies [Mer2, p.326, (14.62)], see [Coh, p.241, l.1-l.9]; Hamilton's equations implies [Mer2, p.326, (14.61)], see [Lan1, p.135, l.6-l.11].
- The beauty of commutator algebra is that we jettison the complicated calculation required with Poisson brackets and preserve its algebraic essence. The reduction greatly simplifies qualitative discussion of physical phenomena. Furthermore, we may apply the commutator algebra and the Schrödinger equation to a microscopic system.
- A wave packet is the wave function of a localized particle [Coh, p.26, l.-11-l.-9].
- The group velocity of the wave packet = the velocity of the (free) particle [Coh, p.29, (C-28)].
- The correspondence principle: the classical value of a physical quantity = the expectation value of the corresponding operator [Schi, p.26, (7.9); p.27, (7.10)].
- Theoretical proof from the wave point of view
(See [Coh, pp.286-289, Complement CIII], where
DQ is the variance of a distribution function).
Remark. Bohr's complementarity principle [Schi, p.8, l.4] can be considered as the physical idea behind the proof. - A precise and simultaneous measurement is physically
impossible because of the interaction between the apparatus and the
measured particle. In this case, Dx
represents inaccuracy.
- Examples.
- Localization experiment.
- [Schi, p.9, l.8-p.10, l.11] or [Eis, p.67, l.-16-p.68, l.-11].
When the momentum of the electron is known, the measurement of its position involves inaccuracy [Schi, p.9, (4.1)] and introduces an uncertainty into the momentum [the Compton effect: Schi, p.9, l.-10].
Remark. In order to separate the scattered photons from the incident beam, the direction of the incident beam should be oriented as in [Schi, p.9, Fig. 2], not [Eis, p.67, Fig. 3-6]. - Diffraction experiment [Hec2, p.5, Fig. 1-1].
When the momentum of the photon is known, the measurement of its position involves inaccuracy [Hec2, p.5, l.6] and introduces an uncertainty into the momentum [Hec2, p.5, (1) & (4)].
- [Schi, p.9, l.8-p.10, l.11] or [Eis, p.67, l.-16-p.68, l.-11].
- Momentum determination experiment [Schi, p.10, l.16-p.11, l.18].
When the position of the particle is known, the measurement of its momentum involves inaccuracy [the Doppler effect: Schi, p.11, (4.8)] and introduces an uncertainty into the position [Schi, p.11, (4.7)]. - Diffraction experiment with photon indicators [Schi, p.12, Fig. 3].
If the interaction between a photon and an indicator were so weak that would not destroy the original diffraction pattern, the uncertainty in py for a particular photon produced by its encounter with an indicator would have to be small, as stipulated in [Schi, p.12, (4.9)]. Because [Schi, p.12, (4.12)] contradicts [Hec2, p.6, (6)], it is impossible to determine through which slit the photons pass without destroying the diffraction pattern [Schi, p.12, l.-12-l.-10].
- Localization experiment.
- Applications.
- The limits of geometric optics [Lan2, p.144, l.-11-l.-1].
- The shell model of many-electron atoms.
[Lev2, p.338, Fig. 11.6] summarizes [Coh, complements AXIV and BXIV]. The central-field approximation [Coh, p.1411, l.-4] explains why we start with electron configurations [Coh, p.1413, (10); p.1414, (11)] and why the interelectronic repulsion can be treated as a perturbation [Coh, p.1412, l.11].
From configuration to terms [Lev2, p.327, Table 11.2]: (a). Equivalent electrons [Lan3, p.254, l.6-l.28; Coh, p.1423, (23)]; (b). Nonequivalent electrons [Lan3, p.254,l.1-l.5]. - The electron gas [ neglect interactions between electrons].
- Free electrons enclosed in a box.
- There is a one-to-one correspondence between the lattice points in the k-space and the wave functions of an electron [Coh, p.1434, l.5-l.7].
- The ground state of the electron system with the Fermi energy [Kit, p.183, l.13]: [Coh, p.1392, l.-5-l.-3]. The definition of the Fermi energy in [Coh, 1435, (6)] is more precise than that of [Kit, p.183, l.13]. Note that Pauli's exclusion principle applies not only to the electron gas [Coh, p.1434, l.-6-l.-1] but also to the electron system of a solid [Coh, p.1443, l.-23; p.1161, Fig.4].
- Periodic boundary conditions.
- The motive of periodic boundary conditions is to simplify calculations [Coh, p.1440, l.-12-p.1441, l.8].
- When the interatomic spacing decreases, the splitting increases because the coupling increases [Coh, p.1159, Fig. 2].
- The stationary states of an individual electron are all delocalized [Coh, p.1159, l.2].
- The deeper the band's location, the more narrow it is [by the tunnel effect; Coh, p.1161, Fig. 4].
- Due to Pauli's exclusion principle, only the electrons with energies close to the Fermi energy are
important for the following applications:
- deriving the correct formula of specific heat for the electron gas.
- deriving the correct formula of magnetic susceptibility for the electron gas.
- explaining why some solids are good electrical conductors while others are insulators.
- Free electrons enclosed in a box.
- Coulomb's law Û Gauss' law [Cor, pp.50-51, (3.19)-(3.22); Sad, pp.126-127, §4.6.A].
- Electric multipoles [Wangs, chap. 8].
- A dipole
- Its potential: [Wangs, p.114, (8-21)].
- Its field: [Wangs, p.120, (8-50)].
- The interaction energy of a dipole in an external electric field: [Wangs, p.127, (8-73)].
Remark. [Wangs, p.124, l.-13-l.-6] gives a physical reason why we are not interested in studying the energy changes of the external charges. - The torque on a dipole in an external electric field: [Wangs, p.127, (8-75)].
- A quadrupole
- Its potential: [Wangs, p.115, (8-30)].
- Its field: [Wangs, p.123, (8-55)].
- The interaction energy of a quadrupole (with an axis of rotational symmetry) in an external electric field: [Wangs, p.130, (8-81)].
Remark 2. If both the monopole moment and the dipole moment are zero, then the quadrupole moment becomes the dominant feature of a charge distribution [Wangs, p.115, l.-17-l.-15].
Remark 3. [Wangs, p.80, (5-48)] is the common background used to build [Wangs, p.99, (7.6)] and [Wangs, p.125, (8-62)]. - A dipole
- Conductors [Wangs,
pp.83-95, chap. 6]
Remark. [Wangs, p.54, (3-13)] can be easily derived using Gauss' law [Jack, p.28, (1.11)].- The outward force p per unit area at the surface of the conductor is the
product of the surface charge density
and the external electric field [Jack, p.43, l.2-l.4].
Proof. The electric field Esheet generated by a sheet charge distribution is s/2e0 above the sheet and is
- (s/2e0) below the sheet [Wangs, p.54, (3-13)]. In order to let Etotal satisfy [Wangs, p.83, (6-1); p.85, (6-4)], we must add Eexternal = s/2e0 to Esheet. The field Esheet locally generally by the sheet cannot exert a force on itself, therefore p = s Eexternal = s2/2e0. - Electrostatic screening [Wangs, p.87, l.-3].
- Systems of conductors [Wangs, §6-2,
§6-3; Chou, p.90, l.9-p.94, l.2].
Remark. The definition of [Wangs, p.89, (8-12)] depends on the particular point chosen on the ith conductor [Wangs, p.88, l.19-l.20]. In order to prove the uniqueness of pij's and the existence of cij's, we must use the uniqueness theorem [Chou, p.91, l.-2-l.-1] to establish the one-to-one correspondence between F and Q [Chou, p.91, (2.138)]. Note that [Wangs, (6-12)] has the advantage that it can be easily translated to a computer program if the surface charge density distribution is known. Actually, [Chou, p.92, l.-10-l.-5] shows not only the non-singularity but also the positive-definiteness of the (pij). As for the proof of the fact that (pij) and (Cij) are symmetric, I prefer [Wangs, p.89, l.-6-p.90, l.13] to [Chou, p.93, l.5-p.94. l.2]. The former proof is constructive and insightful, while the latter proof uses formalism.
- The outward force p per unit area at the surface of the conductor is the
product of the surface charge density
and the external electric field [Jack, p.43, l.2-l.4].
- Electrostatic energy [Wangs, §7-3,
§7-4 §10-8,
§10-9].
- A system of charges [Wangs, p.99, (7-10)].
- A system of conductors [Wangs, pp.100-101, §7-2].
- An electric field [Wangs, p.102, (7-28)].
- Electrostatic forces on conductors [Wangs, p.107, l.15-p.108, l.7].
- The discussion of electrostatic energy is divided into two classes: constant free charge (if the system is isolated) and constant potential difference (if the system is connected to an external energy source) [Wangs, p.105, l.8-p.106, l.-10; p.165, l.11-l.22].
- Boundary conditions.
- Static
electric fields
- dielectric-dielectric [Sad, p.183, Fig. 5.10)].
- conductor-dielectric [Sad, p.185, Fig. 5.12].
- Potential continuity between two media [Wangs, p.139, (9-20)].
- Potential discontinuity across a dipole layer [Jack, p.34, (1-27) or "§Potential of Uniform Dipole Layer" in <http://web.mit.edu/6.013_book/www/chapter4/4.5.html>].
- Steady conduction currents: [Wangs, p.136, (9-21) & p.209, (12-26)].
- Static
electric fields
-
- (Equilibrium)
A perfect conductor cannot contain an electric field below its surface [Sad, 165, Fig. 5.2]. - (From disturbance to equilibrium)
The relaxation time of a conductor (dielectric) after introducing charge at some interior point [Sad, p.181, (5.49)].
- (Equilibrium)
- Biot-Savart's law [Sad, pp.263-266, §7.2]
Û Ampère's
circuital law (Proof. Þ:
[Wangs, pp.237-241] or [Jack, pp.178-179, §5.3]. Ü:
[Sad, pp.274-275, §7.4.A].
Remark 1. In proving Ampère's circuital law, [Wangs, pp.237-241] uses the line integral [Wangs, p.225, (14-2)] for B, while [Jack, pp.178-179, §5.3] uses the volume integral [Jack, p.178, (5.14)] for B. The steps of reasoning in Wangsness' proof can easily conjure accompanied physical images, while those of Jackson's cannot.
Remark 2. In proving Ampère's circuital law Þ Biot-Savart's law, we must assume knowledge of the direction of B due to a current [Wangs, p.242, l.-7] in order to find the magnitude of B. Thus, we have used a bit of information of Biot-Savart's law to derive the entirety of Biot-Savart's law. Therefore, strictly speaking, Biot-Savart's law and Ampère's circuital law are not exactly equivalent. - Magnetic multipoles [Wangs, chap. 19].
- A
magnetic dipole [Cor, pp.337-340].
- Its potential: [Wangs, p.302, (19-22)].
- Its induction: [Wangs, p.302, (19-24)].
- The interaction energy of a magnetic dipole in an external magnetic induction: [Wangs, p.306, (19-36); p.307, (19-40)].
- The torque on a magnetic dipole in an external magnetic induction: [Hall, pp.541-543, §30-4; Wangs, p.308, (19-42)].
- A
magnetic dipole [Cor, pp.337-340].
- Magnetic energy
[Wangs, chap. 18; §20-6; Jack,
§5.16].
- Magnetic forces on circuits: [Wangs, pp.290-295,
§18-3].
Remark 1. It is better to use [Cor, p.480, l.5] to explain the second of the three equalities in [Wangs, p.291, (18-38)].
Remark 2. Wangsness uses the sign of a magnetic force alone to determine whether the force is attractive or repulsive [Wangs, p.293, l.22; p.295, l.13]. His strategy is very confusing. However, if we follow Corson's method by considering the dot product of the magnetic force and the infinitesimal displacement [Cor, p.480, (26-37)], then it will become much easier to determine whether the force is attractive or repulsive.
Remark 3. The discussion of electrostatic forces on conductors [Wangs, p.104, Fig. 7.1] is divided into two cases: constant charge and constant potential difference. The discussion of magnetic forces on circuits [Wangs, §18-3] is divided into two cases: constant currents and constant flux [Wangs, p.218, Fig. 13-1]. At first glance, the divisions seem to depend on the devices we choose. In fact, if we look deeply into the matter, the choices of divisions are fundamentally determined by the characteristics of fields [Fan, p.75, l.23-l.25]. The divisions cannot be made different regardless of device. - [Chou, p.286, l.6-l.10] explains why the second integral of [Jack, p.213, (5.146)] vanishes without any extra assumption [Jack, p.213, l.-11].
In order to fully understand the concept of magnetic energy, we must perform a series of clarifications and comparisons.
- (Total magnetic energy vs. interaction energy) [Wangs, pp.285-286, Example].
- (System: a single circuit with constant current I) If the flux change through the circuit is dF, then the work done by the sources (of current) is dW=I dF [Jack, p.212, l.-11].
- (System: a steady-state current distribution [Jack, Fig. (5.20)]) The total increment work done against the induced
emf
[Wangs, p.284, l.-9] by external sources due to a change
dA or dB is [Jack, (5.144)
or (5.147)]. The total work [magnetic energy] to bring the fields (of the
system) up from zero to their final values is [Jack, (5.148)].
Remark. dA or dB refers to the change of the system made by external sources. - (System: a permanent magnetic moment) Compare [Jack, (5.150)] with [Jack,
(5.72)] [Jack, p.214, l.-4-p.215, l.3].
Remark. Note that before placing [Jack, p.214, l.7] the magnetic moment in the external field, the magnetization M in [Jack, (5.150)] does not exist [Jack, p.215, l.2]. - The discussion of magnetic energy is divided into two classes: constant currents (if the system
is connected to an external energy source) and constant flux (if the system is
isolated) [Wangs, p.290, l.-22-p.292, l.5; Jack,
p.214, l.-16-l.-5].
Remark. Whenever we speak of a flux, we must specify the current source that produces the flux. Without such a specification, people may wonder whether DF in [Chou, p.282, l.-6] includes the flux from self-inductance.
- Magnetic forces on circuits: [Wangs, pp.290-295,
§18-3].
- Boundary conditions [Sad, p.331, (8.41); p.332, (8.45)].
- (General case) In lossy dielectrics [Sad, pp.417-422, §10.3].
- (Special cases)
- Plane waves in lossless dielectrics [Sad, p.423, §10.4].
- Plane waves in good conductors [Sad, pp.425-428; §10.6].
- The Laue condition: Constructive interference occurs if and only if
Dk is a reciprocal lattice vector.
Proof. Þ: [Kit2, p.35, l.-6].
Ü: [Ashc, p.98, (6.4)-(6.7)]. - The Ewald construction of diffraction peaks [Ashc, pp.101-104].
- The Laue method using a range of wave lengths.
- The rotating-crystal method.
- The powder (randomly oriented grains) method.
- From the viewpoint of equilibrium [Go2, pp.16-21,
§1-4]
The key idea: (D'Alembert's principle) The infinitesimal work [F-(dP/dt)]·dr is zero [Go2, p.17, (1-44)] when the system is nearly in equilibrium.
The procedure:- Eliminate the appearance of the forces of constraints [Go2, p.18, l.8].
- Transform the constraint coordinates to the generalized coordinates [Go2, p.18, l.10].
- From the viewpoint of action [Fom, §9
& §21].
The key idea: (Hamilton's principle) The infinitesimal action change is zero near the actual path. In other words, the action integral along the actual path [Go2, p.36, (2-1)] is stationary.
The construction of normal coordinates in [Kit2, p.639, (5)] is much simpler than that in [Sym, pp.469-471, §12.3] or that in [Lan1, p.68]. I would like to try to explain why Kittel's construction is a natural way to decouple the equation of motion [Kit2, p.641, (19)] and the total energy [Kit2, p.641, (21)] even though my explanation is not precise and complete.
- The reciprocal lattice corresponds to the basis of the Fourier expansion of a periodic function [Kit2, p.32, (5)].
- There is a one-to-one correspondence between the lattice points and the reciprocal lattice points [Ashc, p.87, l.-18].
- The energy of a harmonic oscillator is quantized by its frequency [Coh, p.494, (B-34)].
- The direct enumeration of all the wavelike solutions [Hoo, p.37, (2.8)] can be viewed as a method of decoupling [Hoo, p.38, l.17; p.40, l.11-l.16; Kit2, p.101, Fig. 5] even though decoupling the equation of motion is traditionally considered the first step toward finding the solutions.
- The dispersion relation [Hoo, p.38, (2.9); Kit2, p.640, (15)] is the major link between [Hoo, p.37, (2.8)] and [Kit2, p.639, (5)].
- The uncertainty principle implies that the Fourier transforms of two strongly-coupled, broad wave packets in position space are two distantly-separated, narrow wave packets in momentum space. Thus, the use of Fourier transforms facilitates the decoupling process of equations of motion in a lattice.
Remark 2. [Mari, p.501, (12.142)] is an extremely powerful device for decoupling (see [Mari, p.501, l.-1]).
Remark 3. In [Rei, p.408, l.22], Reif says that the concept of normal variables reduces the complicated problem of interacting atoms to the equivalent problem of noninteracting harmonic oscillators. However, he only justifies his statement from the viewpoint of energy [Rei, p.408, (10.1.8)]. In fact, whenever we call certain variables normal variables we must routinely test whether they satisfy the following requirements in classical and quantum mechanics.
- The requirements in classical mechanics.
- Decouple the total energy [Coh, p.580, (20)]: Express the total energy in
terms of the energies which can be associated with each of the modes.
Examples. [Coh, p.596, (47) & (50)] (when x and p are considered as normal variables); [Coh, p.597, (52) & (53)] (when a is considered as a normal variable). - Decouple the equations of motion [Coh, p.577, (11)].
- Decouple the total energy [Coh, p.580, (20)]: Express the total energy in
terms of the energies which can be associated with each of the modes.
- The requirements in quantum mechanics.
- Decouple the total energy [Coh, p.600, (76) & (77)].
- Decouple the equations of motion [Kit2, p.641, (19)].
- Redecompose the state space as the tensor product of eigenspaces [Coh, pp.583-584, §c; especially, p.583, l.2-l.3]: The old component eigenspace is not invariant under the coupling operator [Coh, p.598, l.-6-l.-5]. We must redecompose the state space as a tensor product of new eigenspaces ([Coh, p.600, (79)] define the new ground state. The new tensor product can be generated by creation operators [Coh, p.600, l.-11].)
- The uncertainty principle [Coh, p.597, (54)].
- Any pair of component operators corresponding to different modes commute: Position and momentum operators [Coh, pp.581-582, (26)-(31); p.597, (54)]; annihilation and creation operators [Coh, p.600, (72-a)]; the total Hamiltonian [Coh, p.600, (79)].
- bound states: the energies are bounded [Coh, p.357, l.3] and discrete [Coh, p.354, l.-10].
Energy bands for a periodic potential [Coh, p.372, Fig. 2 & p.379, Fig. 4].
Remark 1.
Remark 2. At this general stage, we can only have a qualitative (i. e. geometric) analysis
for the big picture. For
example, we can discuss the structure of its reciprocal lattice. As the case
becomes more specific, more physical meanings can be precisely
associated with [Coh, p.379, Fig. 4].
Remark 3. How an energy gap arises (the mathematical (quantum) explanation
(Energy gaps must exist somewhere, but we cannot pinpoint their locations.): matching conditions [Coh,
p.369. l.-8; Eis, p.p.458, l.-15];
the physical explanations (At a zone boundary, the symmetric wavefuncton and
the antisymmetric have different energies.): qualitative [Eis, p.459, l.-6-p.460,
l.18]; quantitative [Kit2, p.179, (6)]).
- The general theory of an electron in a solid: The main feature of this
approach is that the Hamiltonian is not specified [Coh, pp.1161-1168,
Complement FXI,
§2]. The Hamiltonian can refer to a free electron or an electron bound
to an atom.
- The allowed energy band: [Coh, p.1163, (9) & Fig. 5].
- Stationary states: Bloch functions [Coh, p.1164, (14), (15), and (16)].
Remark. The delocalization of the electron: [Coh, p.410, (C-20)] ®
[Coh, p.1159, l.2] ® [Coh, p.1164, (17)].
- Nearly free electron theory [Hoo, pp.100-104,
§4.1].
Remarks.
- We can only focus on one theory at a time. Aiming at too many goals will
lead nowhere. [Ashc, chap. 9] and [Kit2, chap. 7] assume that their readers do
not have a background in perturbation
theory, so they try to develop both perturbation theory and nearly free
electron theory at the same time. It turns out that both approaches fail to
provide a clear picture of energy bands. For example, n in [Hoo, p.102, (4.4)]
is associated with the standing wavefunction sin(npx/a)
[Hoo, p.102, l.14] and the n-th term of the Fourier expansion of the
potential. In contrast, the meaning of n in [Kit2, p.187, l.-18]
and [Ashc, p.162, l.17] is not as specific enough as it could be. I like Hook's approach because it
focuses on nearly free electron theory and assumes that his readers have a
background in perturbation theory. Furthermore, I prefer having a complete understanding of
a 1-dim lattice to
having a vague picture of a 3-dim lattice [Ashc, pp.152-166].
- Hook's approach
shows insight. Although his approach is not perfect, it is amenable to
improvements.
- We may use [Kit2, p.183, l.13] to prove that the only important term in
the lattice potential of [Hoo, p.101, (4.2)] is V1cos(2px/a)
[Hoo, p.129, l.11].
- We may use [Ashc, pp.155-156, Case 2] to prove that y has the form
aeikx+bei(k-2p/a)x [Hoo, p.129, l.13;
Ashc, p.156, (9.22)].
- [Kit2, p.179, (6)] is not as good as [Hoo, p.102, (4.4) & (4.5)] because
the former only calculates the energy gap of the first band, while the latter
calculates the energy gap of the n-th band for every n.
- The tight binding approximation [Iba, pp.137-142,
§7.3; Ashc, pp.176-184, §General formulation;
§Application to an s-band from a single
atomic s-level].
Remark 1. The caption of [Coh, p.1161, Fig.4] gives a more fundamental
reason than that given in [Iba, p.141, ii)] to explain why a deep lying band
is narrower than the shadow lying band.
Remark 2. Both [Abr, p.10, (1.21)] and [Iba, 139, (7.31)] are based on the Ritz method [Iba, p.139, l.13]. Although the latter formula is more
intuitive, the former formula has the following advantages: (1). The inversion
theorem [Ru2, p.199, Theorem 9.11]; (2). The complicated computation given in [Abr, p.10, (1.23)] is
actually a simple consequence of
[Ru2, p.202, (13)], a fact that Abrikosov probably did not recognize. [Kit2, pp.245-248, §Tight
binding method for energy bands] fails to fully use these advantages of
Fourier analysis. Note that [Abr, p.10, (1.21)] is based on [Ru2, p.192,
(4)], but the physical interpretations of the two formulas can be different:
The domain of wn is cleverly preserved as the
position space, while the domain of f^ is often interpreted as the momentum space (The
position variable disappears because it becomes the dummy variable of
integration).
Remark 3. A scholar should not just discuss trivialities and avoid discussing
difficult issues by pretending not to see them. Most textbooks in solid state
physics fail to
explain why g(R) in [Ashc, p.182, l.-9]
is the same constant for each of the atom's 12 nearest neighbors. Some of the
above books still lack
any improvement on this point even after many editions. [Ashc] is one
exception. However, Ashcroft gives only a vague hint
[Ashc, p.182, l.-12-l.-9].
Ashcroft's argument would be clarified if he were to add that he uses the formula [Ru2, p.186,
§8.27, (1)].
- The H2+ ion-covalent bonding [Hoo, pp.111-115,
§4.3.2].
-
The physical meaning of the limits of the first allowed band is given by [Hoo, p.114, Fig.
4.7(a); Coh, p.1159, Fig.2 & p.1179, (48)].
- Quantum resonance: [Coh, p.1177, l.-15-l.-9].
- The origin and stability of the chemical bond [Coh, p.1179, l.-15-l.-6].
- The way to improve the result of the variational method is to enlarge the
family of trial kets [Coh, p.1182, l.-9; p.1183,
Table I; p.1173, Fig. 2].
- A 1-dim chain.
The physical meaning of the n-th band refers to the n-th principal quantum
number for a single atom [Ashc, p.183, Fig. 10.4].
Remark 4. The physical meaning of [Ashc, p.141, (8.50)] is given by [Hoo, p.116, l.-6-p.117, l.6].
Remark 5. Both nearly free electron theory and the tight binding approach have similar dispersion
relations [Hoo, p.119, l.-17-p.120, l.-8].
[Iba, p.106, Fig. 6.1] explains why the results derived from the two theories
are consistent.
Remark 6. A scholar should be brave enough to face a challenge and should
not sweep what he does not understand under the rug. [Cra, p.8, l.9-l.17;
Ashc, p.140, footnote 17] explain why E(k) is a continuous function of k. In
contrast, [Kit2, chap.7 & chap.9] and [Abr, chap. 1] do not even mention such a
problem. Unless he or she is extremely careful, an average reader will not be able to
detect these authors have left out something important.
- The allowed energy band: [Coh, p.1163, (9) & Fig. 5].
- Stationary states: Bloch functions [Coh, p.1164, (14), (15), and (16)].
Remark. The delocalization of the electron: [Coh, p.410, (C-20)] ® [Coh, p.1159, l.2] ® [Coh, p.1164, (17)].
Remarks.
- We can only focus on one theory at a time. Aiming at too many goals will lead nowhere. [Ashc, chap. 9] and [Kit2, chap. 7] assume that their readers do not have a background in perturbation theory, so they try to develop both perturbation theory and nearly free electron theory at the same time. It turns out that both approaches fail to provide a clear picture of energy bands. For example, n in [Hoo, p.102, (4.4)] is associated with the standing wavefunction sin(npx/a) [Hoo, p.102, l.14] and the n-th term of the Fourier expansion of the potential. In contrast, the meaning of n in [Kit2, p.187, l.-18] and [Ashc, p.162, l.17] is not as specific enough as it could be. I like Hook's approach because it focuses on nearly free electron theory and assumes that his readers have a background in perturbation theory. Furthermore, I prefer having a complete understanding of a 1-dim lattice to having a vague picture of a 3-dim lattice [Ashc, pp.152-166].
- Hook's approach
shows insight. Although his approach is not perfect, it is amenable to
improvements.
- We may use [Kit2, p.183, l.13] to prove that the only important term in the lattice potential of [Hoo, p.101, (4.2)] is V1cos(2px/a) [Hoo, p.129, l.11].
- We may use [Ashc, pp.155-156, Case 2] to prove that y has the form aeikx+bei(k-2p/a)x [Hoo, p.129, l.13; Ashc, p.156, (9.22)].
- [Kit2, p.179, (6)] is not as good as [Hoo, p.102, (4.4) & (4.5)] because the former only calculates the energy gap of the first band, while the latter calculates the energy gap of the n-th band for every n.
Remark 1. The caption of [Coh, p.1161, Fig.4] gives a more fundamental reason than that given in [Iba, p.141, ii)] to explain why a deep lying band is narrower than the shadow lying band.
Remark 2. Both [Abr, p.10, (1.21)] and [Iba, 139, (7.31)] are based on the Ritz method [Iba, p.139, l.13]. Although the latter formula is more intuitive, the former formula has the following advantages: (1). The inversion theorem [Ru2, p.199, Theorem 9.11]; (2). The complicated computation given in [Abr, p.10, (1.23)] is actually a simple consequence of [Ru2, p.202, (13)], a fact that Abrikosov probably did not recognize. [Kit2, pp.245-248, §Tight binding method for energy bands] fails to fully use these advantages of Fourier analysis. Note that [Abr, p.10, (1.21)] is based on [Ru2, p.192, (4)], but the physical interpretations of the two formulas can be different: The domain of wn is cleverly preserved as the position space, while the domain of f^ is often interpreted as the momentum space (The position variable disappears because it becomes the dummy variable of integration).
Remark 3. A scholar should not just discuss trivialities and avoid discussing difficult issues by pretending not to see them. Most textbooks in solid state physics fail to explain why g(R) in [Ashc, p.182, l.-9] is the same constant for each of the atom's 12 nearest neighbors. Some of the above books still lack any improvement on this point even after many editions. [Ashc] is one exception. However, Ashcroft gives only a vague hint [Ashc, p.182, l.-12-l.-9]. Ashcroft's argument would be clarified if he were to add that he uses the formula [Ru2, p.186, §8.27, (1)].
- The H2+ ion-covalent bonding [Hoo, pp.111-115,
§4.3.2].
- The physical meaning of the limits of the first allowed band is given by [Hoo, p.114, Fig. 4.7(a); Coh, p.1159, Fig.2 & p.1179, (48)].
- Quantum resonance: [Coh, p.1177, l.-15-l.-9].
- The origin and stability of the chemical bond [Coh, p.1179, l.-15-l.-6].
- The way to improve the result of the variational method is to enlarge the family of trial kets [Coh, p.1182, l.-9; p.1183, Table I; p.1173, Fig. 2].
- A 1-dim chain.
The physical meaning of the n-th band refers to the n-th principal quantum number for a single atom [Ashc, p.183, Fig. 10.4].
- Faraday's observations [Jack, p.208, l.-16-l.-6].
- For a static situation, there is no connection between the electric field and the magnetic field. Faraday's law of induction establishes their connection only for a nonstatic situation [Wangs, p.263, l.-27-l.-23].
- Sometimes we define flux as the product of density and velocity [Wangs, p.393, l.3-l.6]; sometimes we define flux as the dot product of a vector field and an area (e.g, the magnetic flux [Wangs, p.251, (16.6)]). What is the relationship between these two ideas? Answer: [Coh, p.238, l.20-21]. Thus, a generalized concept keeps only a small number of the properties of its original concept.
- Electromotive force [Hall, pp.518-519, §29-1]; Lenz's law [Hall. pp.577-579, §32-3; p.580, l.25-l.30; Wangs, p.264, l.-17-p.265, l.-10].
- Faraday's law written in the form of [Wangs, p.272, (17-30)] is independent of the motion of the medium [Wangs, p.272, l.9].
- [Jack, p.210, (5.137)] is [Chou, p.251, (6.18)]. Its proof is given in [Chou, §6.3]. d/dt in [Chou, p.251, l.5] refers to a fixed charge (particle) in the moving circuit (fluid). For its physical meaning, see [Lan6, p.3, l.1-l.3]. ¶/¶t refers to a fixed point in space. For its physical meaning, see [Sym, p.313, l.25-l.26; l.-3-l.-1]. The argument given in [Chou, §6.3] follows closely the formalism given in [Chou, Appendix I] which has well established physical interpretations. The proof given in [Wangs, §17-3] is well tailored to this particular problem, and is simple, direct, and clear in the mathematical sense. However, there is a gap in the deduction from [Wangs, p.271, (17-25)] to [Wangs, (17-26)]. The gap can be filled using [Jack, p.209, l.-15-l.-5] ([Wangs, p.266, (17-8)] is invariant under the Galilean transformation when v <<c) or using the argument in [Cor, §23.2 & §23.7] ([Cor, (23-28)] is invariant under the Lorentz transformation [Cor, (23-61)] when v's magnitude is comparable to that of c).
- A has only a jˆ component
[Wangs, p.260, Fig. 16-6]. Inside the solenoid, A is given by [Wangs, p.259,
(16-49)]. Outside the solenoid, A is given by [Wangs, p.259, (16-50)].
Remark. [Cor, p.350, l.5] gives a direct physical reason why A¹0 outside the solenoid. - By symmetry, B is independent of z and of j [Cor, p.355, l.9].
Br=
0 [Cor, p.355, l.14]. Inside the
solenoid, Bj
is given by [Cor, p.356, l.15] and Bz
is given by [Wangs, p.260, l.-5]. Outside the
solenoid, Bj
is given by [Cor, p.356, l.11] and Bz
is given by [Wangs, p.260, l.-4].
Remark. The direct physical reason why Bz=0 outside the solenoid can be attributed to the following two facts: 1. [Wangs, p.226, l.23]. 2. The denominator of the integrand in [Wang, p.227, (14-11)] is large.
- Proofs
- First proof [Ashc, pp.133-135; Kit2, pp.179-180].
- The Hamiltonian is periodic [Ashc, p.134, l.16]. (Proof. Let y=x+R. Then ¶/¶y=¶/¶x.)
- Considering the lattice symmetry [Hoo, p.328, l.-9-l.-4], we must require that the wave function satisfy [Kit2, p.160, (8)]. [Ashc, p.134, l.26-l.30] shows that this physical requirement is theoretically feasible. If the wave function is degenerate, there will be some difficulty in proving [Ashc, p.134, (8.12)], but this difficulty can be overcome by the method indicated in [Coh, pp.141-142, (ii)]. Thus, the first proof is still valid even without Kittel's extra assumption that yk is nondegenerate [Kit2, p.179, l.-3-l.-2].
- The proof given in [Tin, p.38, (3-26)] is also based on the idea of diagonalization, but its discussion is limited to a special case [Tin, p.38, l.11-l.14. Here, the group of the Schrödinger equation [Tin, p.33, l.-11] must be cyclic] and uses the language of the group representation theory.
- Second proof [Ashc, pp.137-139; Kit2, pp.183-185].
- The Fourier series expansion of the wave function: [Ashc, p.137, (8.30)], where {q}=all the values of the wavevector permitted
by the Born-Von Karman boundary conditions (see [Ashc, p.136, (8.27)]; [Kit2,
p.183, (25)]).
Remark. For the physical origin of the Born-Von Karman boundary conditions, see [Iba, p.83, l.-8-p.84, l.9]. The advantage of the Born-Von Karman boundary conditions is that we can base our discussion of a finite crystal on the model of an infinite crystal [Ashc, p.136, (8.27)] rather than restart the discussion from scratch ([Coh, Complement OIII partially repeats the discussion of [Coh, Complement FXI]) - Decouple the family of {cq} in [Ashc, p.137, (8.30) into subfamilies ck+K [Ashc, p.138, l.-11], where k's are defined by [Ashc, p.136, (8.27)]. We label the decoupled wave function y as yk [Kit2, p.184, l.7-l.10]. [Kit2, p.235, l.-9-l.-3] and [Hoo, p.330, l.-13-l.-7; p.331, l.-7-p.332, l.-1]-332, §11.4.1] say the same thing, but Kittel's formulation is more concise and precise.
- The Fourier series expansion of the wave function: [Ashc, p.137, (8.30)], where {q}=all the values of the wavevector permitted
by the Born-Von Karman boundary conditions (see [Ashc, p.136, (8.27)]; [Kit2,
p.183, (25)]).
- Third proof [Coh, p.1162,l.1-p.1164, l.-4].
- First proof [Ashc, pp.133-135; Kit2, pp.179-180].
- The dashed curves in [Ashc, p.133, Fig. 8.1] are derived from [Coh, p.790, (C-4)].
- The crystal momentum is not the electronic momentum [Ashc, p.139, (8.45); Kit2, p.205, (11)].
- [Ashc, p.141, (8.50)] is clearly explained by the labeling scheme in A.b.ii. The steps in A.b.ii pinpoint the reason why the second proof allows the yk to be degenerate [Kit2, p.185, l.-1].
- The origin of the set {enk
| where k is fixed and n is any integer} in
[Ashc, p.141, (8.50)].
- From the viewpoint of eigenvalues: the roots of the determinant of [Kit2, p.187, (32)].
- From the viewpoint of eigenfunctions: [Cra, p.13, l.5-l.7].
- The essential ideas of the above three proofs are the same (decoupling). The second proof uses Fourier analysis to convert the equation of motion into decoupled linear systems of algebraic equations. The first proof uses linear algebra to find a basis to simultaneously diagonalize the Hamiltonian and translation operators. The third proof specifies the wavefunction [Coh, p.1164, (13)] and is a special case of the first proof [Coh, p.1164, l.-2-p.1165, l.19].
- Empty lattice approximation [Kit2, p.188, l.-4-p.189, l.-7]: let the potential functions Un(x) ® 0 uniformly in x as n®+¥; the displacements indicated in the caption of [Kit2, p.236, Fig. 3] are justified by [Kit2, p.237, (2)].
- In the case of no near degeneracy, by [Ashc, p.155, (9.13)], the shift in energy from the free electron value is second order in U [Ashc, p.155, l.9].
- In the nearly degenerate case, by [Ashc, p.156, (9.19)], the shift in energy from the free electron value is linear in U [Ashc, p.155, l.10].
- Through the careful estimation from [Ashc, p.155, (9.16)], we shift our attention
from [Ashc, p.152, (9.2)] to [Ashc, p.156, (9.19)]. Kittel jumps from [Kit2,
p.186, (31)] to [Kit2, p.191, l.20-l.21] by observing the superficial
similarity between [Kit2, p.177, (5)] and [Kit2, p.191, (49)]. Thus, Kittel's
argument is not as rigorous and careful as Ashcroft's. The argument in [Iba,
p.135, l.-2-p.136, l.19] is also better than
Kittel's.
The reason given in [Hoo, p.101, l.-4] why we should give up the method used for the nondegenerate case is inadequate because the fact that the first-order energy correction=0 should not stop us from pursuing the second-order energy correction. In contrast, [Abr, p.14, l.1-l.8] gives a good reason why we should switch to nondegenerate case. Furthermore, [Abr, p.14, l.9] gives more choices than those given in [Hoo, p.101, l.-2-p.102, l.5] - The caption of [Coh, p.409, Fig. 11] says that the two perturbed levels "repel each other". The meaning of this statement is not clear. In contrast, [Ashc, p.155, l.4-l.7] defines the phrase "two energy levels repel each other" clearly and mathematically.
- The equation of motion in k space of an electron in an energy band.
- in a uniform electronic field: [Kit2, p.204, (4)].
- in a uniform magnetic field: [Kit2, p.204, (7)].
Remark 1. [Kit2, p.204, l.-3-p.205. l.3] illustrates [Ashc, p.229, Fig. 12.6].
Remark 2. The projection of a real space orbit in a plane perpendicular to the field is an orbit of the same shape and rotation direction as the k-space orbit, but rotated 90° around the field direction [Ashc, p.230, l.10-l.13; Hoo, p.375, Fig. 13.7].
- A hole.
- wavevector: [Kit2, p.206, (17)].
- energy: [Kit2, p.207, (18)].
- velocity: [Kit2, p. 208, (19)].
- effective mass: [Kit2, p.208, (20)].
- equation of motion: [[Kit2, p.208, (21)].
- Thermal expansion [Iba, pp.91-94, §5.5; Hoo, pp.63-66, §2.7.1].
- Heat conduction by phonons [Iba, pp.94-99, 5.6; Hoo, pp.67-74].
Remark 1. [Hoo, p.69, (2.73)] is the mathematical proof of the physical formulas [Hoo, p.67, (2.68) & (2.69].
Remark 2. [Hoo, p.70, (2.75)] and [Iba, p.96, (5.43)] are the same. The former formula is derived from elementary kinetic theory, while the latter formula is derived from the consideration of the canonical distribution [Rei, p.205, l.10] [1].
Remark 3. Normal processes versus umklapp processes [Hoo, p.67, Fig. 2.17(b) versus Fig. 2,17(c); Iba, p.97, Fig.5.6(a) versus Fig. 5.6(b); Kit2, pp.134-135, Fig. 16a,c versus Fig. 16b,d].
- The tangents in [Iba, p.114, Fig. 6.6 & p.115, Fig. 6.7] help clarify the procedure for estimating the small fraction of the free elections that can absorb thermal energy.
- The estimate in [Hoo, p.82, (3.16)] is better than that of [Iba, p.115, (6.36)]. See [Iba, p.117, (6.46)].
Remark. The tensor design serves to keep the measurement of physical quantities covariant with coordinate transformations so that physical laws will retain the same form.
- The strong equivalence principle [Ken, p.11, l.-12-l.-10;
p.12, l.7].
Remark 1. The strong equivalence principle based on the weak equivalence principle [Ken, p.10, l.-15] is an extension of the first postulate of special relativity [Ken, p.11, l.-6-l.-3].
Remark 2. A frame in free fall can cover the space-time manifold locally but not globally [Ken, p.12, l.3; p.40, l.7-l.-9; Pee, pp.231-233, § The Metric Tensor].
Remark 3. The principle of generalized covariance [Ken, p.63, §6.4] can be considered the tensor version of the strong equivalence principle. - If we express the physical laws in special relativity in terms of tensors,
they will retain the same form in any other accelerated frame. In
particular, if a formula involves derivatives, the derivatives in the
corresponding formula under a coordinate transformation should be replaced by
covariant derivatives [Ken, p.81, l.-15-l.-10].
- Mass affects the metric of the space-time manifold: The Schwarzschild metric
equation [Ken, p.44, (4.10)] reduces to the Minkowski metric equation [Ken,
p.44, l.8] in the limit of zero mass.
Remark 1. Geodesics in (space ® Minkowski space ® curved space-time) [Ken, p.41, l.10-l.18]. The length of a geodesic in space is a minimum, while the length of a geodesic in the space-time of special relativity is a maximum [Ber, p.56, l.4-p.57, l.-5]. This is because the metric tensor in space is positive definite, while the metric tensor in space-time is indefinite.
Remark 2. The Schwarzschild metric tensor can be derived from [Pee, p.271, (10.84); p.273, (10.92)]. Another proof can be found in [Ken, p.15, l.-3-p.17, l.15; Ber, p.75, l.1-l.8]. The first equality in [Ken, p.16, l.12] can be derived from [Rin, p.40, (17.1)]. The second derivation of the Schwarzschild metric tensor can be made rigorous by using Einstein's field equation [Ken, Appendix D, pp.195-196]. - Newton's second law [Ken, p.63, (6.11)].
- The conservation laws of the four vector momentum [Ken, p.81, (7.13)].
- In the Newtonian limit, Einstein's equation [Ken, p.83, (7.19)] will reduce to Newton's law of gravitation [Ken, p.85, l.7].
- Mass affects the metric of the space-time manifold: The Schwarzschild metric
equation [Ken, p.44, (4.10)] reduces to the Minkowski metric equation [Ken,
p.44, l.8] in the limit of zero mass.
- The tangential acceleration vs. the normal acceleration [Cou2, vol. 1, p.396, (41) & (42)].
- It is easier to recognize the outline of electromagnetic properties of matter in [Fur, §2.4] than in [Wangs, pp. 546-568]. Furthermore, few books explain [Fur, p.104, Fig. 2.18] as clearly as [Fur]. However, it is better to study [Kit2, pp.380-392] before one reads [Fur, §2.4]. This is because [Kit2, pp.380-392] provides rigorous definitions of applied electric field, the macroscopic electric field, and the local electric field. The prerequisite to understanding [Kit2, pp.380-392] is [Wangs, chap. 10 and chap. 23].
- For clarity, [Wangs, p.548, Fig. B-1] should be supplemented with [Hall, p.472, Fig. 26-12].
Remark. [Wangs, p.338, l.22-l.32] illustrates the theoretical advantage of using a Rowland ring, while [Cor, p.375, footnote] explains why Rowland rings are no longer used in practice.
- [Ashc, p.466, l.3] To be consistent with the Dulong and Petit law at high temperatures, the area under the theoretical curve gD(w) [Ashc, p.466, l.1] must be the same as that under the experimental curve [Rei, p.410, Fig. 10.1.1].
- [Ashc, p.466, l.4] To obtain the correct specific heat law at low temperatures, the theoretical curve must agree with the experimental curve in the neighborhood of w = 0. Thus, the Debye scheme should adopt the simplification given in [Ashc, p.456, l.1-l.10; Fig. 23.1].
- The energy [Lan1, p.14, l.10], momentum [Lan1, p.17, l.-14-l.-12], and angular momentum [Lan1, p.20, l.-8-p.21, l.9] of a closed system.
- Conservation laws for the energy-momentum tensor of the electromagnetic field:
- Special relativity: [Lan2, p.82, (33.6)].
- General relativity: [Ken, p.81, l.16].
- Conservation of crystal momentum [Ashc, p.786, (M.7)]:
- Isolated insulator [Ashc, p.787, (M.18)].
- Scattering of a neutron by an insulator [Ashc, p.788, (M.22)].
- Isolated metal [Ashc, p.788, l.-7-l.-5].
- Scattering of a neutron by metal [Ashc, p.788, l.-4-p.789, l.2].
Remark 2. In order to understand the precise meaning of Noether's theorem, one needs an elaborate analysis like Sagan's. Compare [Sag, p.120, Definition A2.16] with [Fomi, p.80, Definition].
- The formula for thermal conductivity [Ashc, p.500, (25.30) & (25.31)]. The derivation of the formula can be found in [Rei, p.479, Fig. 12.4.2 (1-dim) ® Ashc, p.500, Fig. 25.3 (3-dim)]. The arrow implies that the basic idea in the two cases is the same.
- The reasons why a perfectly harmonic crystal would have an infinite thermal conductivity.
- The phonon states are stationary states [Ashc, p.496, l.-11]
Û There are no collisions between different phonons
[Kit2, p.133, l.23] (i.e. there is no thermal resistivity).
Remark. The scattering of phonons means that the wave functions of phonons evolve with time. - A nonvanishing mean velocity is given by [Ashc, p.141, (8.51)] (see [Ashc, p.497, footnote 15]). This mean velocity is not driven by a temperature gradient [Kit2, p.134, Fig. 16a, l.5].
- [Pei, p.40, (2.56); l.10-l.11].
- The phonon states are stationary states [Ashc, p.496, l.-11]
Û There are no collisions between different phonons
[Kit2, p.133, l.23] (i.e. there is no thermal resistivity).
-
- At high temperatures (T >> QD): [Ashc, p.501, (25.32) & (25.33)].
- At low temperatures (T << QD): As the temperature decreases, the conductivity will increase [Ashc, p.504, (25.40) & p.500, (25.31]. The phonon mean free path will increase up to the length limit imposed by lattice imperfections, impurities, or size. Hence, the phonon mean free path will become independent of temperature. Thus, the temperature dependence of the conductivity is determined by the specific heat. Specifically, the conductivity will rise as T3. The rise will reach a maximum at a temperature where umclapp processes [Ashc, p.502, l.1] become frequent [Ashc, p.504, (25.39)] enough to yield a mean free path shorter [Ashc, p.504, (25.40)] than the temperature-independent one. Beyond this temperature, the conductivity continues to decline as exp(T0/T) [Ashc, p.504, (25.40)] up to temperatures well above QD. After this the exponential decline is quickly replaced by a slow power law [Ashc, p.501, (25.33)].
- The expectation value of the Hamiltonian: [Ashc, p.333, (17.14) or Ost, p.111, (3.2)].
- The Hartree-Fock equations: [Ashc, p.333, (17.15) or Ost, p.114, (3.14)].
Remark. Peebles' oversimplified introduction to this metric [Pee, p.54, (5.9)] fails to stress its insight: the Gaussian curvature is invariant. The proof of Theorema egregium in [Ber, Appendix B, pp.160-163] is awkward. A better proof can be found in [Lau, p.65, Theorem 5.5.1].
- How we synchronize clocks [Rin, p.9, l.-13-l.-9].
- Why the transformation from one inertial frame to another is linear [Rin, p.11, l.17-l.27].
- The analogy between a rotation and a Lorentz transformation [Cou2, vol. I, §4.1.j].
- Reif's approach goes from the easy to the complicated: using average velocity v
to express the collision frequency [Reif, p.470,
(12.2.7)] ® using
the distribution function f(r,v,t) to formulate the Boltzmann equation
[Reif, p.525, (14.3.8)]. In contrast, Huang's approach jumps to the
complicated directly [Hua, chap.3]. Thus, Huang leaves out the following two important
turning points of the theory's development:
Flux: [Reif, p.470, (12.2.6)] ® [Reif, p.497, (13.1.3)].
The Boltzmann equation: [Reif, p.509, (13.6.2)] ® [Reif, p.525, (14.3.7)]. The equivalence [Reif, p.510, l.1] of the two formulations enables us to jump from a crude approach [Reif, p.504, l.3-l.6] to an more accurate approach. - Huang fails to prove du=du' [Hua, p.60, l.-13], while Reif gives a rigorous proof [Reif, p.521, l.15].
- Reif establishes a relationship between s(v1,v2ïv1',v2') and s(W) [Reif, p.520, (14.2.4)], while Huang does not. Therefore, the statement in [Hua, p.69, l.-8] is not clear. Similarly, [Reif, p.524, (14.3.3) is clear, while [Hua, p.66, (3.29)] is not.
- The generalization from an inversion [Reif, p.522, l.1-l.2] to a rotation or reflection [Hua, p.63, l.9-l.10] is unnecessary because it does not have any other useful application than the inverse collision.
- [Reif, p.523, l.-18-l.-15] imposes an essential assumption on f(r,v,t) to justify the format of the mathematical expression in [Hua, p.56, (3.2)]. The reasons given in Huang's justification [Hua, p.56, l.8-l.14] are related, but are not essential.
- The equality in [Hua, p.96, l.8] is derived from [Reif, p.529, (14.4.20)] and its corresponding formula for the inverse collision.
- The Collision frequency: [Reif, p.470, (12.2.7)] is too crude and [Reif, p.470, (12.2.8)] is too sophisticated. [Reic, p.660, (11.14)] gives an appropriate interpretation of the Collision frequency.
- [Hua, p.106, (5.72)] is correct, but Huang's argument for its derivation is incorrect. It would be better to use brute force to calculate each coefficient of Lkl in the summation on the right-hand side of [Hua, p.106, (5.71)].
- (Unifications) The conservation theorem [Hua, p.96, (5.14)] unifies the conservation laws of mass, momentum, and energy [Hua, p.98, (5.21)-(5.23)]. Huang derives the conservation theorem from the Boltzmann transport equation [Hua, p.67, (3.36)], which involves the concept of differential cross section. In contrast, [Reic, pp.534-537, §10.B.1] derives the conservation laws of mass, momentum, and energy without using the concept of differential cross section. The entropy source [Reic, p.539, (10.26)] helps define the generalized currents and forces [Reic, p.539, l.-11-l.-5]. Thus, the discussion in [Reic, pp.537-541, §10.B.2] is an indispensable step toward recognizing that transport coefficients are the generalized conductivities of a hydrodynamic system [Reic, p.539, l.-4-p.540, l.1;p.541, l.5-l.10; p.543, (10.29)-(10.31)]. Putting transport coefficients and conductivity into the same category is a kind of unification that stride across different fields.
- Ensemble [Hua, p.141, l.8].
Remark. If we can prove a statement directly, we should not take a detour. [Hua, p.141, (7.6)] can be directly derived from the definition of a partial derivative. Huang's detour approach [Hua, p.141, l.-13-l.-12] indicates that he does not understand the definition of a partial derivative very well. - The density of states [Man, pp.324-335, Appendix B].
Remark. [Man, p.334, (B-38)] can be proved using [Kit2, p.87, Fig. 18]. - A system in a heat bath [Man, pp.52-64, §2.5].
Remark 1. The proof of [Man, p.57, (2.29)] can be found in [Reif, p.213, (6.5.8)].
Remark 2. We need not repeat the historical approach. The classical method of counting states must be fully justified in terms of quantum mechanics. Compare [Reif, p.51, l.8-l.16] with [Man, p.174, l.-7-l.-1]. - Fluctuations
- Energy [Reif, p.110, (3.7.14); p.213, (6.5.8) or Man, p.58, (2.31) (the canonical ensemble)].
- Occupation numbers [Hua, p.82, (4.54) (the ideal gas)].
- The canonical ensemble evolves from the microcanonical ensemble:
- The drawback of the microcanonical ensemble with respect to calculations [Hua, p.153, l.7-l.12].
- The new constraint imposed on the canonical ensemble [Hua, p.157, l.2-l.4].
- The ideal gas.
Remark 1. When considering ideal gases, the first thing one has to do is to throw away all the world's documents about ideal gases. One should study only [Reif, §9.1, §9.2, §9.6, §9.7, §9.8, §9.10], except for any discussions about Maxwell-Boltzmann statistics they contain. If one needs the required background on quantum mechanics, one should read only [Coh, §XIV,C.3.d]. This approach relieves one of the burden of studying a tremendous amount of incorrect physics. To stop the practice of torturing physics students, the future authors of physics textbooks should follow my advice.
Remark 2. Mandl points out that [Hua, p.146, (7.22)] is based on [Hua, p.152, (7.52)]. However, Mandl's strategy to prove [Man, p.188, (7.70)] does not work. It is better to follow Huang's calculation scheme [Hua, p.152, l.9-l.10].
Remark 3. In classical mechanics, a rigorous definition of physical states [Coh, p.1392, (C-9)] for a system of identical particles does not exist. Therefore, for the partition function of the ideal gas, the classical method of counting states requires a correction when compared with the correct quantum result. The only book in classical mechanics that contains a clear definition of a macrostate is [Zem, p.279, l.11], but the concept is borrowed from quantum mechanics. The goal of counting states in classical mechanics is to lead to a rigorous definition of physical states. A good classical method of counting states should facilitate accomplishment of this goal. For example, the first term of [Man, p.168, (7.9)] corresponds to [Coh, p.1390, (C-11)] and the second term of [Man, p.168, (7.8)] corresponds to [Coh, p.1390, (C-10)] (up to the normalization factor). Even so, the classical derivation of [Man, p.169, (7.10)] is not as rigorous as the quantum mechanical derivation of [Reif, p.361, (0.10.3)]. - (Paramagnetism) The discrepancy between [Reif, p.208, (6.3.7)] and [Pat, p.81, (14)] is due to different averaging methods. The former averages the magnetic susceptibility over the two spin states [Reif, p.207, (6.3.3)], while the latter averages the magnetic susceptibility over all solid angles [Pat, p.80, (7)].
- (Microcanonical ensemble) Reichl fails to explain why CN
= N! h3N in [Reic, p.348, (7.16)]. N! can be
explained using the strategy given in [Reic, p.359, l.8]. h3N
can be explained by [Man, p.174, l.-1]. Similarly,
Huang fails to explain the Gibbs correction factor in [Hua, p.195,
(9.42)]. Intrinsically, Microcannonical ensemble is a classical design. Its
shortcomings are discussed in [Man, p.182, l.9-l.18]. The problem with [Hua,
§9.5] is that Huang throws quantum
particles into a classical design without explaining why it is justifiable to
do so. A theory should be built with its essential features. Building a theory should not be like making a
pizza with every topping on it. it should not involve throwing all the knowledge into one pot. A
cumbersome theory that has no
application or that is designed to solve every problem is trash. Even just looking at [Hua, p.194, Fig. 9.1] makes
one dizzy. The discussion that goes with this figure is even more confusing.
One should apply a method in a
flexible manner instead of being entrapped in its mathematical structures.
Furthermore, a model
should be as simple as possible. Consequently, the discussion of an
ideal gas in [Reic, p.348, Exercise 7.2] is better than that in [Hua, p.196,
l.-3-p.197, l.16]. The same remark applies to [Pat,
§6.1], Cliff's notes of [Hua].
Remark. Landau uses the fact that levels broaden into bands [Lan5, p.15, l.12; p.22, l.-12-l.-9] to explain why the microcanonical ensemble, a classical design, still applies to quantum statistics. - The grand partition function
- The justification of the definition given in [Hua, p.190, (9.27)]: [Reif, p.347, l.1-l.18].
- Its simplified relationship with the partition function [Reif, p.347, (9.6.6)].
- Equalities [Hua, p.198, (9.61) & l.-3-l.-1].
- Links {1}.
- Einstein's gravitational field equation [Pee, p.268, (10.65)] ® Gravitational field equations for nonrelativistic material [Pee, p.269, (10.69); Rin, p.103, l.12-l.14].
- Electromagnetic field equations [Rin, p.103, (38.3); p.104, (38.5) & (38.7)] Û the Maxwell equations [Rin, p.107, (38.20), (38.21) & (38.23)].
- The Lorentz relation [Chou, p.76, (2.92)].
- The Clausius Mossotti relation [Chou, p.76, (2.95)].
- Electronic polarization (induced dipoles) [Chou, p.77, (a); p.78, (2.96)].
- Orientation polarization (permanent dipoles) [Chou, p.77, (b); p.79, (2.101)].
- Formal solutions of the Poisson equation [Chou, p.31, l.-2-p.32, l.9].
- The existence of solutions of the Poisson equation with Dirichlet or Neumann boundary conditions [Chou, §3.2].
- The uniqueness of solutions of the Poisson equation with Dirichlet or
Neumann boundary conditions [Chou,
§3.2].
Remark 1. The assumptions of this problem are carefully written in [Chou, §3.1]. The argument in [Jack, §1.9] cannot be considered rigorous because Jackson fails to state these assumptions clearly.
Remark 2. All of the following statements are justified by the uniqueness theorem.- [Chou, p.115, l.-10-l.-8].
- [Chou, p.117, l.2-l.5].
- [Chou, p.120, l.1-l.2].
- The method of images [Chou, §3.4; Sad,
§6.6; Jack, §2.1-§2.5]].
- The image charge must be external to the region of interest [Jack, p.57, l.-9-l.-8].
- The solution of the Poisson equation is provided by the sum of the potentials of the charges inside the region of interest [Jack, p.57, l.-6-l.-5].
Remark 2. [Sad, p.240, l.9-p.241, l.6] provides a piece of general guidance that helps to solve boundary-value problems using the method of images. This guidance, based on experiences, can only be described by guidelines rather than specific details. The success of applying these guidelines relies on one's skill and experiences.
Although guidelines are valuable advice, they do not guarantee the success of problem solving. Driving is an example. Driver A with ten year experience is accident free now. Driver B just received his driver license for the first time. Even if Driver A gives Driver B good guidelines about safe driving, the latter still has to go through many accidents during the first year to learn to become a safe driver. Similarly, to become a skilful problem solver, one has to practice constantly and compile new guidelines from one's own experiences. [Lau, p.67, l.12-l.16] provides another interesting example. - Complex-variable methods [Chou, §3.5].
- Conformal representation [Chou, §3.6].
- Solutions for the spherical boundary conditions: [Jack, §2.6].
- Boundary-value problems with azimuthal symmetry
- Dielectric sphere in a previously uniform electric field: [Cor, pp.231-233, Example], [Wangs, pp.194-197, Example] and [Chou, pp.148-150, (ii)] all give the formula of the electrostatic potential. Of the three proofs of this formula, Corson's proof is the best. His concept is clear and his analysis is rigorous. In [Wangs, p.197, Fig. 11-13], Wangsness says the lines belong to the E field. In fact, they belong to the D field (see [Cor, p.232, Fig. 12-2]).
- A useful device: [Jack, p.101, l.-2-p.104,
l.4].
Remark 1. Although Jackson elegantly uses the uniqueness theorem to prove [Jack, p.102, (3.38)], the proof of [Wangs, p.112, (8-12)] is a natural approach which links Legendre polynomials more closely to their generating function [Guo, §5.3].
Remark 2. Although Jackson applies the device only to the boundary-value problems, the key idea of this device is actually based on [Ru2, p.226, Corollary].
- Mixed boundary conditions (e.g., conducting plane with a circular hole) [Jack,
§3.13}
Remark. The equations of [Jack, p.132, (3.179)] can be solved using [Guo, p.406, (8) & (9)]. - Boundary-value problems with dielectrics [Jack,
§4.4].
Remark. For a plane, we use the method of images [Jack, p.154, l.-2-p.157, l.9]; for a sphere or spherical cavity, we use separation of variables in spherical coordinates and expand the solution in a series using the basis of the Legendre polynomials. These methods are essentially the same as those of finding the green functions [1].
- The Ewald-Oseen extinction theorem [Born,
p.101, l.4-l.7]
The dipole field is the sum of two terms [Born, p.102, (21)]: one cancels out the incident wave [Born, p.102, (23)], whereas the other satisfies the wave equation with velocity c/n [Born, p.100, (10)].
Remark 1. (Internal references) The validity of the statement in [Born, p.101, l.4-l.7] is not well documented, so one may not catch its meanings immediately until one finishes reading [Born, §2.4.2]. However, if Born had pointed out where the readers can find the proof for each phrase of the statement in this long section [Born, §2.4.2] as I did above, the readers would catch the meaning at the first reading and would have a clearer picture for understanding the rest of material in [Born, §2.4.2]. The mathematics textbooks written by N. Bourbaki are famous for their internal references: The validity of almost every statement is well documented whether the proof is given before the statement or after.
Remark 2. For various electric fields in dielectrics only [Kit2, pp.380-392] provides clear definitions. Therefore, it is important to identify the effective field E' in [Born, p.85, l.23] with the local field Elocal in [Kit2, p.386, (14)] or the polarizing field Ep (producing the displacement of charges) in [Wangs, p.547, l.-14] and identify the mean field E in [Born, p.85, l.24] with the total macroscopic electric field E in [Kit2, p.384, (7)].
Remark 3. The assumption [Born, p.104, (32)] is not used in [Born, p.104, l.8-p.107, l.12]. [Born, p.104, (32)] is proved by [Born, p.107, (49); p.105, (41)] with the assumption [Born, p.104, (33)]. The purpose of presenting [Born, p.104, (32)] before its proof is to help create [Born, p.104, Fig. 2.4] so that we know what is going on.
Remark 4. The extinction theorem provides the insightful relationship between the incident field and the dipole field. This relationship based on the microscopic viewpoint (dipoles) is so powerful that it can be used to derive both the law of refraction [Born, p.107, (52)] and the Fresnel formulae [Born, p.107, (55a) & (55b)]. - Molecular polarizability and electric susceptibility [Jack,
§4.5]
- The Clausius-Mossotti equation [Jack, p.162, (4.70)].
- The Lorentz-Lorenz equation [Jack, p.162, l.-1].
Remark. [Born, p.87, (17)] serves to link the microscopic quantity a [Born, p.92, (30)] to the macroscopic phenomena (e and n). The Lorentz-Lorenz equation implies that the refractive index depends on frequency [Born, p.92, (31)]. The proof given in [Born, §2.3.3] is valid only for the first approximation [Born, p.85, l.12]. In contrast, the proof given in [Born, §2.4.2] is rigorously derived from an integral equation concerning polarization [Born, p.100, (4)].
- Electrostatic Energy in dielectric media [Jack,
§4.7].
Remark. The material in [Jack, p.166, l.-2-p.167, l.17] is treated by Jackson as part of the content of his advanced textbook. However, in [Wangs, p.164, l.1-l.4], Wangsness treats the same material as an exercise of his elementary textbook. It is too difficult for the reader of an elementary textbook to encounter an exercise that is accorded extensive coverage in an advanced textbook. There is difference between writing a paper and doing an exercise. Similarly, it is not proper to put an exercise from an elementary textbook into the content of an advanced textbook. Considering the intended reader, it is clear that one of the above two authors must be seriously wrong.
E I;W = E near;J and
E;J = E p;W - E i;J
= (E ;W + E O;W + E I;W) - (E near;J - E P;J)
= E ;W + E O;W + E P;J .
The above comparison is only a temporary remedy. In the future, we must unify the terminology in this area so that physicists can speak the same language.
The proof of [Jack, p.189, (5.69)] is incorrect. The notation m´Ñ in [Jack, p.189, (5.67)] is problematic. This notation is not defined in any math textbook because multiplication and differentiation are not commutative: m(¶f/¶x)¹¶(mf)/¶x. Furthermore, [Jack, p.189, (5.68)] is incorrect. For a correct formula of Ñ(m×B), see [Wangs, p.34, (1-112)]. Thus, [Jack, p.189, (5.67)] should have been
Fi = S eijk[m´ÑBk(0)]j; [Jack, p.189, (5.68)] should have been
F = m´(Ñ´B) + (m×Ñ)B = Ñ(m×B).
Remark 1. Jackson's serious mistakes reveal the urgent need to strengthen the teaching staff in today's institution of American higher education.
Remark 2. Using [Chou, p.214, (5.62)], Choudhury gives an elegant proof of [Chou, p.214, (5.63)].
Remark 3. There is no inconsistency between [Jack, p.189, (5.69)] and [Wangs, p.537, (A-35]. We can use [Wangs, p.533, (A-20)] to explain why the two formulae look different.
- A classical treatment [Jack, p.190, (5.73)].
- A quantum mechanical treatment [Coh, pp.1247-1256, Complement A XII].
Remark 2. [Jack, p.145, l.-7-p.146, l.-5] gives a rigorous proof of the statement in [Coh, p.1066, l.6].
Remark 3. The formula given in [Coh, p.1249, l.-2] and the formula given in [Jack, p.190, l.-7] are the same. The latter formula is derived from [Jack, p.176, (5.5)] by replacing the x in [Jack, p.175, Fig. 5.1] with -x (where x is the position of the electron).
Remark 4. [Jack, p.190, l.-13-l.-11] tells us what the hyperfine interaction is, while [Coh, p.1248, (5)] traces to the origin of the hyperfine interaction.
A substance with permanent magnetization: B and H [Jack, §5.10].
- Without an external field [Jack, p.198, (5.105) & (5.106)].
- In an external field [Jack, p.200, (5.112)].
ò [0, a] = ò [0, r] + ò [r, a]. The difficulty of the method using the vector potential [Jack, p.199, l.-12-p.200, l.6] lies in calculating the curl. The method given in [Jack, p.198, l.6-l.-1] does not have these difficulties, so it is the simplest.- A paramagnetic or diamagnetic substance: the magnetization is the result of the application of an external field [Jack, p.200, (5.115)].
- A ferromagnetic substance: the phenomenon of hysteresis allows the creation of permanent magnets
[Jack, p.201, Fig. 5.12].
Remark. For the basics of hysteresis, see [Sad, p.328, l.5-p.329, l.-1].
- Analogies between a conductor and a body with high permeability
- The field lines outside and near to the surface [Jack, p.201, l.-17-l.-15].
- Cavities [Jack, p.201, l.-15-l.-13].
- The dipole moment and the inner field [Jack, p.202, (5.121); p.203, Fig.5.14].
Remark. The discussion of surface tension in [Zem, §2-9 & §3-8] is ambiguous. and raises many questions. The above two web sites will help answer your questions.
- Thermodynamic equilibrium [Zem, §1-5 & §2-1]; equations of state [Zem, §2-5; §2-8-§2-12]; macroscopic states and thermodynamic variables [Zem, p.26].
- Quasi-static transformations [Hua1, p.4, (f)]. In order to
warrant the use of an equation of state, we must perform a quasi-static
process. Methods of performing a quasi-static process [Zem, p.51, l.-9-l.-8;
p.56, l.14-l.16; p.57, l.6-l.7; p.85, l.-14-l.-4].
Remark. Slow free expansion is quasi-static [Hua1, p.4, l.11-l.12]; fast free expansion is not quasi-static [Zem, p.113, l.11]. - Reversible transformations
- Adiabatic reversibility [Zem, §7-1-§7-7].
- Reversibility involving heat transfer: reversibility in this case refers to the universe [Zem, p.85, l.-13-l.-4; §8-5-§8.6].
- Ideal-gas temperature = Kelvin temperature [Zem, §7-8-§7-11].
The following three statements are equivalent:
- No process is possible whose sole result is the absorption of heat from a reservoir and the conversion of this heat into work.
- No process is possible whose sole result is the transfer of heat from a cooler to hotter body.
- Whenever an irreversible process takes place the entropy of the universe increases.
A Þ C [Zem, §8-5-§8-8].
C Þ B [Man, p.115, l.-9-l.-1].
Remark 1. If you compare [Zem, p.154, 1] with [Hua1, p.10, l.-18-l.-7], one can easily find that T1 in [Hua1, p.10, l.-8] should have been T2. This error remained undetected through two editions of [Hua1] (1963 & 1987). This reveals the fact that in these forty years, either no one reads the publications of MIT professors or no one cares about the books published by MIT professors.
Remark 2. [Hua1, p,19, l.13-l.-6] discusses some subtle points that we should pay attention to when we apply the second law.
The most concise and insightful proof is given by [Reic, p.28, l.5-p.31, l.4]. [Reic, p.30, Fig. 2.5] clarifies the confusion contained in other proofs. The proof of [Zem, p.180, (8-3)] is based on [Zem, p.173, (7-13)]. The inexact differential in [Zem, p.173, (7-13)] has a specific form. The inequality in [Hau1, p.14, l.-8] conveys Clausius' subtle point about the inexact differential đQ. However, the proof of the Clausius theorem in [Hua1, pp.14-15], omits too much detail. A detailed proof using the same argument can be found in http://en.wikipedia.org/wiki/Clausius_theorem.
[Zem, p.247, l.-12] mentions the fact that the vapor pressure P(T) is a function of T only, but does not provide the proof. [Hua1, p.33, (2.3)] does give the proof.
Let us compare [Reif, §8.2, §8.3 and §8.10] with [Zem, §14-8]. Note that [Zem, §14-7] emphasizes the following subtle points:
- Even though the initial states of the phases are not in chemical equilibrium, it is still possible to describe them in terms of thermodynamic coordinates. This is because these phases are in mechanical and thermal equilibrium [Zem, p.366, l.11-l.17].
- The functions that express the properties of a phase when it is not in chemical equilibrium must reduce to those for thermodynamic equilibrium when the equilibrium values of the n's are substituted [Zem, p.388, l.-7-l.-4]. In other words, in thermodynamic equilibrium the n's are fixed values, but when the system is not in chemical equilibrium, these n's are variables.
Remark 2. The proof of [Reif, p.314, (8.7.18)] is excellent, while the proof given in [Zem, p.372, l.-7-p.373, l.6] is very confusing.
- Without chemical reaction [Zem, §16-2 & §16-3].
- With chemical reaction [Zem, §16-4 & §16-5].
- Why do we use cavity radiation to represent black-body radiation?
Because
- Cavity radiation is in thermal equilibrium so that the thermodynamic coordinates can be defined [Man, p.246, l.-15].
- A small hole in a wall has the same absorbing and emitting power as a black-body. Key idea: [Man, p.246, l.-6-l.-3]. Proof: [Zem, p.91, (4-17)].
- [Man, Appendix B] proves the formula for the density of states using both particle [Man, §B.2] and wave [Man, §B.3] approaches. [Man, §10.3] proves Planck's law using both the particle and wave approaches.
- In order to prove Wien's displacement law, [Reif, §9.13] obtains the maximum by drawing the graph of the function [Reif, p.375, Fig. 9.13.1], while [Zem, §17-14] obtains the maximum using calculus.
- Planck's radiation equation [Zem, p.446, (17-27)] reduces to
- The Rayleigh-Jeans law [Man, p.253, (10.21)] or the equipartition theorem [Man, p.253, l.-6] in the limit of low frequencies.
- Wien's law [Man, p.254, (10.23)] in the limit of high frequencies.
- We may prove the formula for radiation pressure [Zem, p.451, (17-32)] using
- The kinetic theory [Zem, p.451, l.9-l.-1].
- The partition function [Man, p.255, l.5-p.256, l.11].
Remark 2. [Man, Appendix B] gives a comprehensive discussion on the density of states. There are two points worth noting: First, the density of states is independent of boundary conditions [Man, p.330, l.1-l.2]. Second, the discussion of density of states naturally leads us from the wave equation [Man, p.324, (B-1)] to the Schrödinger equation [Man, p.331, l.-6-l.-2; Reif, p.353, l.-3-p.354, l.9].
Remark. [Wangs, p.276, l.15-p.277, l.8] can be used as a stepping stone to understand the two examples in [Cor, pp.399-404].
Remark. [Wangs, p.450, l.-2-p.451, l.8] discusses the physical significance of the neglect of the displacement current from the viewpoint of energy loss and the viewpoint of the time needed for propagation of signals, while [Chou, p.255, l.15-p.256, l.2] discusses the physical significance from the latter viewpoint alone.
Remark 1. Both Jackson and Choudhury call the details of the proof gory [Jack, p.255, l.-10; Chou, p.304, l.-1]. If this trivial proof is considered gory, I wonder what adjective should be used to describe Tycho Brahe's or Kepler's work.
Remark 2. A formula should be written in its simplest form. [Chou, p.309, (7.44)] can still be reduced to [Jack, p.256, (6.96)]. Both [Chou, p.309, (7.44)] and [Jack, p.256, (6.96)] are incorrect as they stand. Sn should have been inserted in front of Sr,s in [Chou, p.309, l.2]. The expression inside the [ ] in [Jack, p.256, l.7] should have been (Qn')ag(vn)b-(Qn')gb(vn)a.
[Chou, p.315, l.3-l.7] can be directly derived from [Chou, p.585, l.3-l.4]. The argument in [Chou, p.314, l.6-p.315, l.1] basically repeats the argument in [Chou, p.584, l.7-p.585, l.1].
- In order to decouple the equations of motion [Hoo, p.38, l.17], we transform from the position space [Hoo, p.37, (2.7)] to the momentum space [Hoo, p.38, (2.9); Man, p.324, (B.1)] using [Hoo, p.37, (2.8); Man, p.330, (B.19)]. This method of finding normal coordinates has a physical origin [Hoo, p.39, Fig. 2.5]. [Kit, pp.102-106] fails to point out the main purpose of phonons: decoupling the equations of motion.
- In the one dimensional case, g(w) is given by [Hoo, p.53, (2.33)]; the assumption w = vS k is equivalent [Hoo, p.59, l.20-22] to taking g(w) as given by the broken line on [Hoo, p.54, Fig. 2.11].
- [Wu, p.45, (I-17)] is easier to derive and evaluate than [Man, p.160, (6.27)].
Remark. Some earlier editions of this book use summation instead of integration. I never like this practice. After I read [Sea1, §9-6, §9-7], I realized that the presentation of the 6th edition using integration is much better than [Hall, §12-5] or anything about moment of inertia existing on the web.
[Coh, chap.VII, §C.3.c] gives a detailed explanation. [Mer, p.266, l.-14 & l.-12] make a few improvements.
[Rob, p.21] discusses the Doppler effect from the viewpoint of time dilation. [Matv, p.33, l.1-l.36] uses the tensor approach. The tensor approach automatically shows that all the formulas on relativity are covariant with Lorentz transformations, and effectively leads to a quick answer. It also condenses three cases (The source is moving toward the observer, away from the observer, or along a line normal to the line to the observer) into one formula [Matv, p.33, (2.62)]. However, Matveev's approach is not as insightful as Bobinson's approach. For example, it is easier to see that [Matv, p.33, (2.65)] is a purely time dilation effect from the context of [Rob, p.21] than that of [Matv, p.33, l.14-l.36].
[Hec, §4.8; Wangs, §24-3 & §25-6; Matv, p.120, §Color of bodies, Sec. 19 & Sec. 20] discuss the optical properties of metals. All the above books facilitate our understanding in some aspects, but none of their discussion are complete. We must piece together their discussions to see the entire picture.
- Color of gold: For a chunk of gold, we can only see the reflected light [Wangs, p.423, l.-2-l.-1; Hec, p.131, l.c., l.-14-l.-11]. By [Hec. p.129, r.c., l.-12-l.-8], the gold appears reddish yellow. When the light source is on the other side of a thin foil of gold, we can only see the transmitted light, so the gold appears greenish [Wangs, p.423, l.14-l.20].
- Some alkali metals are transparent to ultraviolet [Hec, p.129, l.-3-p.130,
l.c., l.19].
Remark. For the proof of wp = (Nqe2/e0me)1/2, see [Wangs, p.401, (24-138)]. - A metal (s =
+¥) is an extension of an dielectric (s
= 0).
- The dispersion equation (compare [Hec, p.71, (3.72)] with [Hec, p.129, (4.79)]).
- For plane waves, insulators and conductors are two extreme limiting cases and have corresponding discussions [Wangs, p.387, l.10-p.388, l.-12].
- Any problem in geometrical optics can be solved either using formulas or using graphs. The latter method not only has the visual advantage, but also can be used as a check for calculations from the former method. Example: [Jen, pp.86-87, Example 2].
-
- Virtual objects
- Illustrated in a figure: [Hec, p.155, Fig. 5.11].
- Described in words: An object is virtual when the rays converge toward it [Hec, p.155, r.c., l.-7-l.-6].
- Characterized by the object distance: so < 0 [Hec, p.163, Table 5.2].
- Virtual images
- Illustrated in figures: [Hec, p.152, Fig. 5.5(c); p.155, Fig. 5.10].
- Described in words: An image is virtual when the rays diverge from it [Hec, p.155, r.c., l.-8-l.-7].
- Characterized by the image distance: si < 0 [Hec, p.163, Table 5.2].
- Virtual objects
- Only after understanding the meaning of [Jen, p.55, Fig. 3J] may one understand the construction of [Hec, p.151, Fig.5.3(a)].
- Comparing the proof of [Jen, p.56, (3n)] with the proof of [Hec, p.154, (5.8)]: Although the former proof is simpler, the latter proof is more methodological.
- If m>0, the image will be virtual [Jen, p.54, l.15]. This can be seen by [Morg, p.30, (2.11)(ii); Jen, p.49, Fig. 3E].
- The focal plane of a lens [Hec, p.160, Fig. 5.17 (where the radius of s is determined by [p.155, (5.10)]), and Fig. 5.18].
- Geometrical optics uses a lot of modeling. By comparing the arrangement of sections in [Jen, chap. 3] and that in [Jen, chap. 4], we see that the theory of thin lenses is parallel to the theory of refracting surfaces. The theory of spherical mirrors is a special case of the theory of lenses [Morg, p.35, l.18]. The following three theories-thin lenses, thin-lens combinations, and thick lenses- are parallel because they use the same parallel-ray method to form images (compare [Jen, p.69, Fig. 4H] with [Jen, p.80, Fig. 5B(b)]; compare [Jen, p.75, Fig. 4M] with [Jen, p.83, Fig. 5E]). Consequently, the corresponding formulas in these three theories are the same if we properly choose the reference points. For example, [Jen, p.84, (5k)] and [Morg, p.67, (5.24)] can be considered identical. A systematic approach to the problems in geometrical optics entails mastering all the above patterns.
- A system of lenses can be treated as a thick lens [Morg, p.67, l.-7-l.-1].
- Treating mirrors as lenses
- Reflection is considered as refraction [Matv, p.163, l.4-l.14].
- (Sign conventions) Identify [Hec, p.184, Table 5.4] with the combination of [Hec, p.154, Table 5.1] and [Hec, p.183, Table 5.2].
- (Properties) Apply the same graphical constructions used for lenses to mirrors (e.g., identify [Jen, p.101, Fig. 6E] with [Jen, p.63, 4D]; ray 8 in [Jen, p.106, Fig. 6I] is constructed based on [Jen, p.47, Fig. 3C]), apply the same formulas for lenses to mirrors, and identify [Hec, p.185, Table 5.5] with [Hec, p.163, Table 5.3].
- Thick mirrors [Jen, §6.5] can be considered as thick lenses.
- For a detailed and systematic study of the effects of stops, see [Jen, chap. 7].
- In [Hec, §6.2], the method of ray tracing applies only to paraxial rays. That is, it is used only for the first-order approximation. Actually, in principle, the graphical method of ray tracing [Jen, chap. 8] and the matrix method [Jen, p.143] can be exact.
- [Matv. Sec. 21-Sec. 23] condense geometrical optics into 21 pages and are ready for practical application using computers. In addition, Matveev proves every statement that he presents in these sections. His rigorous reasoning and ability to organize are impressive. In contrast, [Hec, chap.5 & chap. 6] use 132 pages to discuss geometrical optics and leave many statements unproved (e.g., [Hec, (6.1)-(6.4); (6.34); (6.36)-(6.37)]). In one place, Hecht claims he has proved [Hec, (6.34)]. Actually, he uses unproven [Hec, (6.2)] to prove [Hec, (6.34)]. Thus, all he has done is state the formula [Hec, (6.2)] twice. For a detailed proof, see [Matv, p.167, (23.19)]. However, logic is not the only tool to facilitate our understanding. For example, the definitions of principle points in [Matv, p.166, l.-1] is not as good as the definitions given in [Hec, p.243, Fig. 6.1]. The graphical constructions given [Jen, §3.6 and §3.7] should not be deemphasized for they have an visual advantage. Matrix methods are a useful tool only for computer calculations. A tool is used when needed. If we use methods to discuss topics other than computer calculations, the tool will become a burden rather than an advantage. In view of [Fur, chap. 3], the theory of geometrical optics are indeed made more organized and compact by the matrix method. All the necessary information on rays is essentially contained in a single matrix. However, the theory's formulation given in [Fur, §3.1-§3.4] is not as well prepared for application [Fur, §3.5] as that given in [Hec, §5.1-§5.6] for application [Hec, §5.7].
- [Hec, p.154, (5.8)] is derived from Fermat's principle, while [Fur, p.145, (3.26)] is derived from Snell's law. Although both approaches consider a bundle of rays, the latter approach is more natural and straightforward.
- Superposition of two plane waves [Born, p.19, Fig. 1.5].
- Superposition of oscillations with equidistant frequencies [Matv, p.97, Fig. 53].
- Group velocity: the velocity of the maximum of the wave packet [Coh, p.30, (C-31); Fig. 6].
- In vacuum or microscopic fields: [Fur, p.44, l.6-l.9].
- In matter (macroscopic fields)
- Average over a volume that is macroscopically small but microscopically large: [Fur, p.60, l.1-l.4].
- In terms of (controllable) free charges and free current densities: [Fur, p.65, l.14-l.17].
- Suppose rf = 0 and Jf = 0. In terms of the material parameters: [Fur, p.68, l.3-l.6].
- Geometrical light rays [Born, p.114, l.-18-l.-17].
- I = |<S>| [Wangs, p.357, (21-58); Matv, p.61, (7.12)].
- Proofs of the eikonal equation: The proof given in [Born, p.112, l.1-l.9] uses the first-order approximation, while the proof given in [Born p.112, l.16-p.113, l.2] uses the second-order approximation. Therefore, the latter proof is more refined.
- Proofs of the law of refraction
The proof given in [Hec, §4.4.1] is restricted to plane waves and planar interfaces. The method lacks potential to be applied for generalization. The proof given in [Hec, p.107, l.c., l.1-l.14] uses Fermat's principle which is artificial; The proof given in [Jack, §7.3] uses the basis of a vector space which is also artificial. In addition, the way the boundary conditions are used in [Jack, (7.34)] differs from the way they are used in [Born, p.5, Fig. 1.2], which complicates matters. The proof given in [Born, §3.2.2] is the most natural proof because it is directly derived from the boundary conditions. The method meets the requirement for axiomatization: any theorem in electromagnetism should be able to be derived from Maxwell's equations. This enables us to trace the theorem to its source. In addition, the derivation of [Born, p.125, (17)] is the same as that of [Born, p.6, (23)], which is good for unification. Furthermore, the proof given in [Born, §3.2.2] applies to the general case [Born, p.125, l.-11-l.-7]. It is the only proof that establishes a strong link to electromagnetism. I wonder why other textbooks leave out such an insightful proof. - [Born, p.126, (23)] represents a normal congruence; [Born, p.126, (22)] represents a normal rectilinear congruence.
For the proof of the former statement, see [Wea1, vol I, §105]. [Sne, p.21, Theorem 5] provides a proof of the identity given in [Wea1, vol. I, p.202, l.-12].
Remark. In the early twentieth century, the textbooks of optics discussed the topics in differential geometry and the textbooks of differential geometry discussed the topics in optics. Each subject solidified the other's foundation and stimulated the other's growth. Now in the twenty-first century, optics and differential geometry have become mutually exclusive subjects. The textbooks in optics are devoid of questions about differential geometry and the textbooks in differential geometry are devoid of questions about optics.
Proof. Ñf (r,q,f) = (¶f/¶r)r^+r-1(¶f/¶q)q^+(r sin q)-1(¶f/¶f)f^ [Wangs, p.33, (1-102)].
Ñ(|r+n|-1)×(r/r) = Ñ(|r+n|-1)×r^ = ¶(|r+n|-1)/¶r.
ò [0,+¥] ¶(|r+n|-1)/¶r dr = |r+n|-1 úr = 0¥ = -1.¬
Tension per unit width = Constant T; Vertical deflection = w(x,y,t).
Consider the displacement of an element of area dxdy at time t.
x-direction: width = dx; left slope = tan q»q; right slope = q+dq.
q = ¶w/¶x Þ dq = [¶(¶w/¶x)/¶x]dx = (¶2w/¶2x)dx.
Vertical component of the tension in the x-direction: left end: -T(dy) tan » = -T(dy)q; right end: T(dy) (q+dq).
Net vertical force from x-direction tension is T(dy)dq = T(¶2w/¶2x)dxdy.
Similarly, the net vertical force from y-direction tension is T(¶2w/¶2y)dxdy.
Total vertical force on dxdy is T(¶2w/¶2x+¶2w/¶2y)dxdy.
Let r be the mass per unit area. Then (rdxdy)(¶2w/¶2t) = T(¶2w/¶2x+¶2w/¶2y)dxdy.
Therefore, r(¶2w/¶2t) = T(¶2w/¶2x+¶2w/¶2y).
The following figure is viewed along the positive y-direction: