Enter your search terms Submit search form
	Web www.lcwangpress.com

Proofs That Are Divided into a Large Number of Cases in Mechanics

    For a proof that is divided into a large number of cases, most textbook writers simply state the result without proof. However, avoiding the trouble of supplying the proof details is not proper for a scholar to solve the problem. The readers feel as though they are abandoned at sea because they are not given any directions about the proof. They may check some cases when needed, but they may not have a clear idea of how to find a systematic method to get them all. Thus, they fail to complete the proof. Some may say a computer can do this mechanical work. However, a computer can only follow the program; it cannot reduce the original argument to improve the effectiveness of the program. Furthermore, these cases may have similar or different arguments. Therefore, it is important to study the following two questions: How do we organize and classify these cases based on the type of their arguments? How do we find an systematic and effective method to check all the cases without missing any?

1. The zero components of the metric connection [Ken, p.195, l.-10].
   Proof. Consider G^m_sr (m, s, r = 0, 1, 2, 3) [64 cases]. There are 13 cases for the non-zero components of the metric connection [Ken, p.195, l.-9-l.-5]. If any two of {m, s, r} are distinct, then G^m_sr = 0 [24 cases].
   1. m = 0
      1. s = 0, 1, 2, 3.
         G ⁰_ss = 0 [4 cases].
      2. s = 2, 3.
         G⁰_s0 = G⁰_0s = 0 [4 cases].
   2. m = 1
      1. s = 0, 2, 3.
         G¹_s1 = G¹_1s = 0 [6 cases].
   3.  m = 2

      1. s = 0, 1, 2.
         G ²_ss = 0 [3 cases].

         s = 0, 3.
         G²_s2 = G²_2s = 0 [4 cases].

   4. m = 3

      1. s = 0, 1, 2, 3.
         G ³_ss = 0 [4 cases].

         s = 0.
         G³_s3 = G³_3s = 0 [2 cases].

   
   
2. The elements of the Riemann curvature tensor G ^a_bgd [Ken, p.197, l.12-l.19].
   Remark 1. We should not check the cases haphazardly because there are too many cases. Disorganization may easily lead to an incomplete or ineffective count. Only after a systematic and complete count may we discover how easy it is to leave some cases out.
   Remark 2. (Taking advantage of the system's special features) Our task is to check that the claim in [Ken, p.197, l.12-l.19] is correct. It is easier than establishing the claim from scratch. We first assume that it is correct and infer that the nonzero elements are included in cases a = g or a = d. Once we obtain this piece of intelligence, we can easily design a strategy to classify the cases effectively. In other words, in the following solution we will classify the cases with this feature and [Ken, p.189, (B.3)] in mind so that our analysis will follow the texture of the Riemann curvature tensor.
   Remark 3. We display nontrivial cases in order to show cancellations. A nontrivial case means that at least one of the four terms on the right-hand side of [Ken, p.74, (7.3)] is not zero.
   Solution. Consider G ^a_bgd [ 4⁴ = 256 cases]. G ^a_bgg = 0 [64 cases].
   1. Consider G ^a_bad , where (d ¹ a) [48 cases].
      1. 
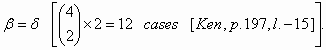         R¹₀₁₀  = -mZ/r³; R²₀₂₀  = R³₀₃₀  = mZ/2r³.
         R⁰₁₀₁  = m/r³Z; R²₁₂₁  = R³₁₃₁  = -m/2r³Z.
         R⁰₂₀₂  = R¹₂₁₂  = -m/2r; R³₂₃₂  = m/r.
         R⁰₃₀₃  = R¹₃₁₃  = -m sin² q /2r; R²₃₂₃  = m sin² q /r.
         
      2. b ¹ d.
         1. b = a [12 cases].
         2. b ¹ a [4´2´3 = 24 cases].
            R³₁₃₂  = G ³_{12, 3} - G ³_{13, 2} + G ³₂₃ G ²₁₂ - G ³₃₂ G ³₁₃
            = 0 - 0 + (cot q)(1/r) - (cot q)(1/r).
            R³₂₃₁  = G ³_{21, 3} - G ³_{23, 1} + G ³₂₃ G ²₂₁ - G ³₃₁ G ³₂₃
             = 0 - 0 + (cot q)(1/r) - (1/r)(cot q).
   2. G ^a_bda = -G ^a_bad [Ken, p.189, (B.3)], where (d ¹ a) [48 cases].
   3. G ^a_bgd = 0, where a ¹ g, d ¹ a and d ¹ g [4´4´3´2 = 96 cases].
      1. a =1.
         R¹₃₃₂ = -R¹₃₂₃ = G ¹_{32, 3} - G ¹_{32, 2} + G ¹₃₃ G ³₃₂ - G ¹₂₂ G ²₃₃
         = 0 - (2r/B) sin q cos q + (-r sin q/B) cot q - (-rB)(-sin q cos q) = 0.
      2. a =2.
         R²₃₃₁ = -R²₃₁₃ = G ²_{31, 3} - G ²_{33, 1} + G ²₃₃ G ³₃₁ - G ²₂₁ G ²₃₃
         = 0 - 0 + (-sin q cos q)(1/r) - (1/r)(-sin q cos q) = 0.
      3. a =3.
          R³₃₁₂ = -R³₃₂₁ = G ³_{32, 1} - G ³_{31, 2} + G ³₃₁ G ³₃₂ - G ³₃₂ G ³₃₁
         =0 - 0 + (1/r) cot q - (cot q)(1/r) = 0.