Video Feedback Oscillator
|
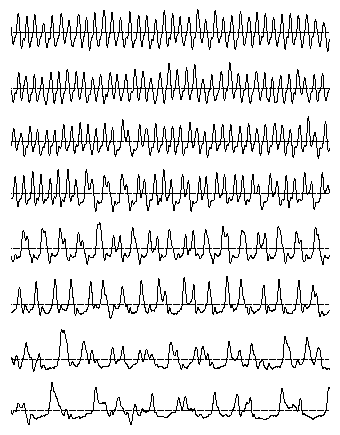
To make the graphs on this page, I turned a video feedback loop into a simple non-linear oscillator, and recorded its behavior as a control (gain, also known as brightness) was adjusted. A video camera was aimed at a monitor displaying the output of the video camera. The camera was rotated slightly and the zoom set so that the image of the monitor was about the same size as the monitor. To create the oscillator, an LED (light emitting diode) was taped to the monitor where the camera could see it. Controls were adjusted so that when the LED went on, it created a pulse of light which cascaded into a large rotating pattern which, left to itself, eventually died out. The input to the LED came from a light sensitive resistor arranged so that when bright light fell on the resistor, the LED would go off, and when no light hit the resistor, the LED would go on. A large magnifying glass focused the image of the entire monitor onto the resistor. Thus when the monitor was dark, the LED would go on, creating a cascade of light in the video feedback loop until the monitor was bright enough to turn the LED off. This oscillation was recorded by digitizing the voltage across the resistor, and filtering to remove the 30 Hz component. Note that the resistor was most sensitive to the red end of the spectrum. In the 8 timeseries shown below, the gain control on the camera was increased from a low setting (top graph) to a high setting (bottom graph). As the gain in the feedback loop increased, the oscillations became more and more irregular. This illustrates the general principle that in a non-linear system, increasing a control parameter can lead the system through various modes of behavior, such as from a periodic to a chaotic pattern.
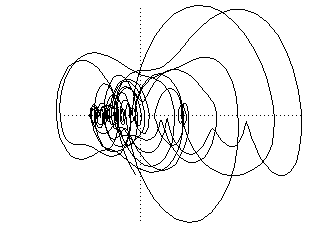
Note that in the third and fourth timeseries, there are still long sections of approximately periodic behavior, with occasional shifts to a slightly different pattern. In the sixth trace, the oscillation has approximately period-doubled. Period doubling is another common property of non-linear systems. Finally the last two traces show highly chaotic behavior. Phase portraits of the first, third, fourth, and eighth timeseries are shown below. A phase portrait plots the data variable on the horizontal axis, and its derivative (or velocity) on the vertical axis. Note how the relatively smooth oscillation of the first phase plot twists and changes into the chaotic pattern of the last plot. |



|
Phase portraits are important in gaining understanding of complex non-linear systems, because they allow a geometrical view of the behavior, and allow identification of critical points in the phase space, such as the point to the left of the vertical axis where the trajectory starts to twist in on itself. Studying the behavior of a system around these points can often lead to an understanding of the global behavior of the system. |