MOTION IN 2 DIMENSIONS
For motion in 2 dimensions we can calculate components of velocity and acceleration by differentiating x and y as functions of time. We can then use Pythagorean Theory to get the total value
PROJECTILE MOTION
SoftBall Projectile Some Observations
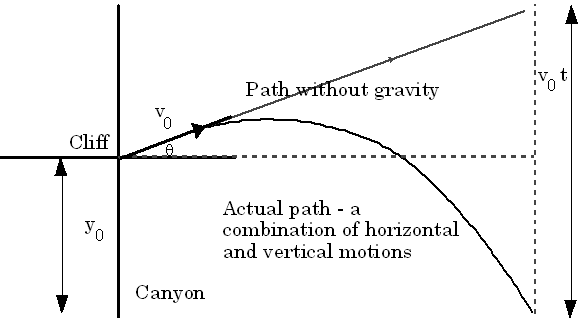
So far we have been dealing with horizontal motion along a straight line and vertical motion along a straight line separately. Here we would like to study motions in a plane such as the motion of a thrown softball or the circular orbit of a satellite.
If a softball is thrown off a cliff with a certain initial velocity in the x-direction and y-direction, it will continue to move forward in the x- direction and at the same time fall in the y-direction as a result of the attraction between the earth and the ball. The two-dimensional motion that a result is known as projectile motion.
Why is it that the projectile keeps the same horizontal velocity?
Jien-Tze Drop and Kick
NAME ____________________________ PARTNER ________________________ DATE _______
PURPOSE
This activity or lab investigates the use of vectors to solve physics problems with the use of a Traditional Taiwanese Toy (Jien-Tze) and a variety of other materials available.
MATERIALS
Assorted Jien-Tze, assorted balls or other materials chosen by students, timing devices, and measurement devices.
Situation A
Karen and Sarah find some Jien-Tze toys near the edge of a cliff in the local park. They know they can calculate the height of the cliff by finding the time it takes the Jien-Tze to fall to the ground and then using the formula d = 1/2gt2. They wonder if the formula will work for a Jien-Tze kicked off the cliff instead of dropped straight down over the edge. Karen and Sarah design an experiment to find the answer. Karen drops one Jien-Tze over the edge at the exact moment Sarah kicks the other Jien-Tze off the cliff.
Make a Prediction
1. Predict which Jien-Tze will hit the ground first - the Jien-Tze dropped over the edge or the Jien-Tze kicked outward off the cliff. Assume there is no air resistance.
Design a method or experimental procedure to confirm or refute your prediction:
2. List the forces acting on each Jien-Tze as it falls. In which direction, x or y, do these forces act?
3. Was your prediction correct? Explain the results in terms of the force vectors acting on each
Jien-Tze.
4. How do the vertical positions of the falling Jien-Tze compare?
5. Using the results of the experimentation and the formula d = 1/2agt2 , calculate the height of the cliff (balcony) you used (ag = 10.00 m/s2).
Situation B
Karen and Sarah now decide to investigate what will happen when one Jien-Tze is thrown vertically upward while the other is kicked upward and outward. Assume both the Jien-Tze have the same initial vertical velocity.
Make a Prediction
6. Predict which Jien-Tze will hit the ground first - the Jien-Tze thrown upward or the Jien-Tze
kicked upward and outward. Assume there is no air resistance.
Design a method or experimental procedure to confirm or refute your prediction:
7. Was your prediction correct? Explain the results in terms of the force vectors acting on each Jien-Tze.
8. Explain what happens to the Force of gravity vector as the Jien-Tze fall.
9. Describe what happens to the Velocity vector for each of the Jien-Tze as they fall. Explain why the Velocity vector for the kicked Jien-Tze changes magnitude and direction during the fall.
Jien-Tze PROJECTILE METHOD (Formal Lab Report)
OBJECTIVE
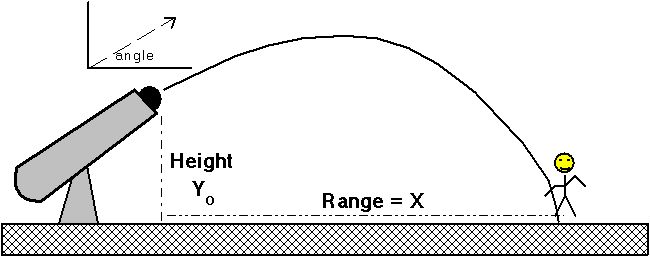
To determine the range of a projectile as a function of projection angle.
MATERIALS
Projectile firing apparatus for use with a Jien-Tze, meter stick or tape measure.
PROCEDURE
STEP 1 Finding the speed of the Jien-Tze
- You probably should do this experiment outdoors (if the weather is cooperative) so that the projectile doesn't hit anything (actually the Jien-Tze won't harm a thing, it's just a nice opportunity to get outside); otherwise an empty hallway may be adequate. Set the firing apparatus on a table or flat surface in such a way that it can be fired at an angle 0o relative to the horizontal. Aim the projectile where it won't hit someone or something. At some angles it will have a range of around 5 meters and a maximum height of nearly 3 meters.
y = yo + vo sin q t - 1/2 agt2 x = xo + vo cos q t
use yo = height then when it hits the ground y = 0
use xo = 0
- Measure the height of the Jien-Tze from the floor. Shoot the Jien-Tze at 0o several times; use the range, X- position when it hits the ground, to find the initial speed of the Jien-Tze.
STEP2 Projected at Same Height as Lands: Measuring Range
- After you have found the initial velocity of the projectile using the table and zero degrees, you will shoot the projectile from ground level and use a box or a few books so that it lands at the same altitude it was shot; yo = yf = 0. Place a piece of tape at the expected impact point, then run two or three trials for each angle in a chart like the one below. Do this for each of the angles (but not zero degrees). Station a lab partner near where the projectile strikes the box. He is to measure the average range of the two or three trials. Measure the average range for each angle of projection and record the data.
STEP3 Projected at Same Height as Lands: Calculating Range
- If you have taken trigonometry, using Trig identities you should be able to show that the range is
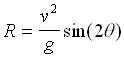
. Use the initial velocity, vo, from procedure 2 above at zero degrees in all your calculations and fill in the Theoretical Displacement in your chart.
Angle Net Vertical Displacement Theoretical Horizontal Displacement Actual Horizontal Displacement 20 30 40 50 60
- On one graph plot both the theoretical and the actual range versus the angle of projection, drawing a smooth curve through each series of points.
STEP 4 Projected from a Cliff: Measuring Range
- For the chart below you will shoot the Jien-Tze from a ledge or table that is at least 80 cm high. Run two or three trials for each angle and record the actual height and range in the chart. [Keep height same throughout]
Angle Net Vertical Displacement Theoretical Horizontal Displacement Actual Horizontal Displacment 20 30 40 50 60 STEP 5 Projected from a Cliff:Calculating Range
- It's too hard to calculate the range in this case, so what we are going to do is to make a table of height vs. time for each angle, and see at what time the projectile hits the ground. Then find the x value at that time.
- On one graph plot both the theoretical and the actual range versus the angle of projection, fitting a smooth curve (parabola) through each series of points.
- From the graph, determine the angle of projection for the maximum range and record the below. Compare with the theoretical prediction of tan q =
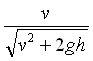
RANGE:
From Actual Graph_________ From Theory Graph _________ From Formulas ______
The essential fact is that all the pictures
which science now draws of nature . . .
are mathematical pictures.
Sir James Jeans
ANALYSIS / CONCLUSIONS
Compare the methods for accuracy and precision. To do this you will need to compare results with several other students. Determine which method is consistently accurate. Explain why this method is both accurate and precise. Why is the theoretical angle for maximum range different from your actual angle? Why is the smaller angle usually more accurate than the larger one? Do a vector analysis for one of the methods utilized in this experimental activity.