Fundamentos De Análisis Vectorial

Indice

1. Algebra de vectores
2. Suma de vectores
3. Diferencia de dos vectores
4. Producto de un vector A por un esclar m
5. Leyes del álgebra de vectores
6. Vector unidad
7. Vectores unidad rectangulares
8. Componente de un vector
9. Producto escalar o interno de dos vectores A y B
10. Leyes del producto escalar
11. Producto vectorial de dos vectores A y B
12. Leyes del producto vectorial

Las magnitudes que intervienen en la mayoría de los campos de las ciencias exactas (particularmente física) pueden clasificarse en 2 clases: los que sólo tienen valor numérico y las que tienen valor numérico, dirección y sentido. De su estudio se facilitan varias nociones para la comprensión abstracta y estudio dimensional de los números.

- Cantidades Escalares.- Son aquellas que quedan determinadas por un número real y, por lo tanto, no tienen dirección. Como ejemplos podemos citar: el tiempo, la masa, la densidad, la longitud, el área, el volumen, la temperatura, el trabajo, la energía, el capital.

Las cantidades escalares se indican por letras de tipo ordinario, como en álgebra elemental. Las operaciones con magnitudes escalares siguen las mismas reglas que en álgebra elemental.

- Cantidades Vectoriales.- Son aquellas que para quedar determinadas precisan un número que exprese su valor absoluto (llamado módulo), una dirección y un sentido, por esto se las llama cantidades dirigidas. Como ejemplos tenemos el desplazamiento, la velocidad, la fuerza, la aceleración.

Gráficamente, una cantidad vectorial se representa por una flecha trazada a escala. La longitud de la flecha representa el módulo, la dirección de la flecha representa la dirección del vector, etc. Un vector tiene siempre un punto O llamado origen del vector y un punto P llamado punto terminal.

Analíticamente, una cantidad vectorial se representa por una letra con una flecha encima y su módulo por el valor absoluto del vector o la letra sin flecha encima. Aquí usaremos el tipo negrita para representar un vector A y |A| o A indican su módulo. De modo similar se puede denotar un vector OP, el cual tiene su origen en O y finaliza en P.

1. Algebra de los Vectores:

Las operaciones de adición, substracción y multiplicación de cantidades escalares (conocidas en álgebra), con una definición conveniente, pueden extenderse al álgebra de vectores. Para este fin debemos conocer las siguientes definiciones:

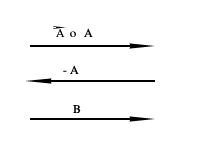
• Dos vectores A y B son iguales si tienen el mismo módulo, dirección y sentido. También son llamados equipolentes. Debemos notar sin embargo, que no necesariamente produciran efectos físicos similares, especialmente en cuerpos rígidos. Esto dependerá de dónde esté situado su origen.
• Un vector que tenga el mismo módulo y dirección que un vector A, pero sentido opuesto, se designa por -A.
• Se llama resultante de un número n de vectores al vector único que produce los mismos efectos que todos los vectores originales juntos.
• Se llama equilibrante de un número n de vectores al vector que equilibra a todos los vectores originales tomados juntos. Este tiene un módulo igual al vector resultante, pero sentido opuesto a éste.

2. Suma de Vectores:

Dados 2 vectores A y B, podemos definir la suma de los 2 como el vector resultante C = A + B. Este se obtiene fácilmente moviendo el vector B a continuación del vector A. Esto se produce a causa da la ley del paralelogramo, que dice: la suma o resultante de dos vectores viene dada en dirección, magnitud y sentido por la diagonal del paralelogramo construido sobre los dos vectores como lados consecutivos.

Esta última definición se extiende a la suma de tres o más vectores: para sumar dos o más vectores, se trazan a escala, unos a continuación de otros, con su propio módulo, dirección y sentido, de modo que el origen de cada uno coincida con el término del anterior. El vector que une el origen del primero con el punto terminal del último es la suma pedida. Esta definición es comunmente llamade la ley del polígono.

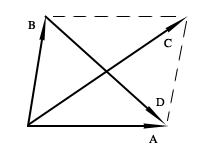
3. Diferencia de dos vectores:

Dados 2 vectores A y B, el vector D = A - B es el vector que sumado con el sustraendo B nos da el minuendo A. Por esto la diferencia de dos vectores esta dada por la diagonal no concurrente del paralelogramo construido sobre los vectores dados como lados consecutivos, tomada esa diagonal en el sentido del sustraendo al minuendo.

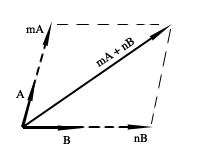
4. Producto de un vector A por un escalar m:

Es un vector mA de módulo |m| veces el módulo de A y con igual sentido u opuesto que el de A, según m sea positivo o negativo. Si m = 0, mA es un vector nulo. Esta definición resulta de sumar m vectores iguales.

5. Leyes del Álgebra de Vectores:

Dados los vectores A, B y C y los valores escalares m y n, se tiene:

1. Ley conmutativa de la adición.- A + B = B + A
2. Ley asociativa de la adición.- A + (B + C) = (A + B) + C
3. Ley conmutativa de la multiplicación.- mA = Am
4. Ley asociativa de la multiplicación.- m (nA) = (mn) A
5. Ley distributiva.- (m + n) A = mA + nA ; m (A + B) = mA + mB

6. Vector Unidad:

Es un vector cuyo módulo vale la unidad. Si A es un vector cuyo módulo es diferente de cero, entonces A/A es un vector unidad que tiene la misma dirección y sentido que A. De la misma manera, cualquier vector A puede representarse por un vector unidad a, tomado en la dirección y sentido de A, multiplicando multiplicado por el módulo de Aí. En simbolos: A = Aa.

7. Vectores Unidad Rectangulares:

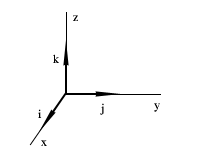
Son importantes los vectores unidad que tienen los sentidos positivos de los ejes OX, OY y OZ de un sistema de coordenadas rectangulares tridimensionales, estos se designan respectivamente por i, j, k.

Emplearemos sistemas de coordenadas dextrorsum, nombre derivado del hecho de que, si un que sacacorchos gira desde OX hacia OY en un ángulo menor a 180º, avanza en el sentido positivo de OZ. Esto se aplica también a tres vectores cuyos orígenes coinciden y no son coplanarios.

8. Componente de un vector:

Una componente de un vector en una dirección dada es su proyección sobre dicha dirección. Por ejemplo: la componente horizontal de un vector es su proyección sobre la dirección horizontal. Un vector puede considerarse como la resultante o suma de sus componentes según las tres direcciones del espacio. Para vectores con origen en O en el sistema dextrorsum tenemos que: A = A1i + A2j + A3k, siendo A1, A2, A3componentes rectangulares de A en las direcciones X, Y, Z, respectivamente.

El módulo de A será entonces: A = raíz cuadrada de (x^2 + y^2 + z^2)

En particular, el vector de posición o radio vector r desde O al punto (x,y,z) se escribe: |r| = xi + yj + zk

9. Producto Escalar o Interno de dos vectores A y B:

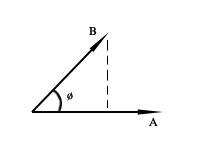
Es el número obtenido multiplicando el producto de sus módulos por el coseno del ángulo comprendido entre ámbos. Se indica poniendo un punto entre los factores. Simbólicamente: A · B = AB cos (ø) ; 0 ≤ ø ≤ π. En otras palabras, el producto escalar de dos vectores es el producto de uno de los vectores por la proyección del otro sobre él.

10. Leyes del Producto Escalar:

1. Ley conmutativa.- El producto escalar de dos vectores es independiente del órden en que se tomen los factores, porque A, B y cos (ø) son tres números. Por esto mismo, siendo A y B módulos, el producto es positivo si ø es agudo, negativo si ø es obtuso y nulo cuando ø = 90º. Dado que el producto puede ser nulo sin que ninguno de los factores lo sea, la división por un vector no puede realizarse.
2. Ley distributiva.- A · (B + C) = A · B + A · C
3. Siendo m un escalar.- m(A · B) = (mA) · B = A · (mB) = (A · B)m
4. Para los vectores unitarios.-i · i = j · j = k · k = 1 ; i · j = j · k = k · i = 0
5. Para componentes rectangulares.-A · B = (A1i + A2j + A3k) · (B1i + B2j + B3k) = A1B1 + A2B2 + A3B3 ; A · A = A1^2 + A2^2 + A3^2

11. Producto Vectorial de dos Vectores A y B:

Es simbolizado por A x B o también [A · B] y es el módulo igual al producto de los módulos por el seno del ángulo que forman los vectores. Simbólicamente: C = A x B = AB sen (ø) ; 0 ≤ ø ≤ π. La dirección de este valor es perpendicular al plano determinado por ambos vectores y cuyo sentido es determinado por el método dextrorsum. Si A = B o si A es paralelo a B, entonces sen (ø) = 0 y A x B = 0.

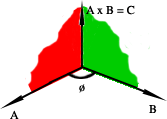
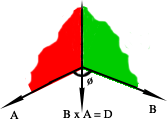
12. Leyes del Producto Vectorial:

Órden de los factores.- A x B = - B x A

Propiedad distributiva.- A x (B x C) = A x B + A x C

Siendo m un escalar.- m (A x B) = mA x B = A x mB = (A x B) m

Vectores unitarios.- Existe una regla simple para estas operaciones: Se escribe la secuencia: "i j k i j" y si el producto va hacia la derecha será positivo, si va a la izquierda será negativo. El valor es el que le sigue según el caso. Por ejemplo: j x k está yendo hacia la derecha en nuestra secuencia, por lo tanto será positivo e igual a i. De manera análoga: j x i va vacia la izquierda en la secuencia, por lo tanto será negativo e igual a k.

Determinantes: A x B puede calcularse por el determinante:

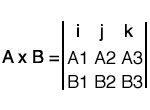
El módulo de A x B vale lo mismo que el área de un paralelogramo cuyos lados son A y B.

Si A x B = 0 y A y B son vectores no nulos, entonces A y B son paralelos.

2004 :: Frank Veverka A. | Información