The Angle between a Line and a Plane; an application of the Angle between two Lines

Problem:

Find the angle between the line parallel to the vector [2, -1, 0] and the plane given by the vector equation r.[3, 0, 4]  = 5
A diagram of this is shown on the right. 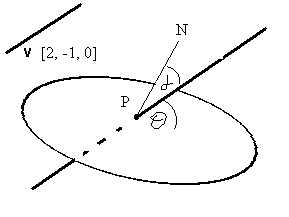v is the vector to which the line is parallel.

P is the point of intersection of the line and plane.

N is the normal to the plane through P.

θ is the angle between the line and plane.

α is the angle between the normal and the line.
The angle, α, between the normal and the line can be easily found using  'the angle between two lines'  method.

The required angle, θ, is then the difference between α and one rightangle.



From the equation to the given plane, r.[3, 0, 4]  = 5, the normal to the plane is parallel to the vector [3, 0, 4]. The line is parallel to the vector [2, -1, 0].

The angle between the normal to the plane and line is therefore, the angle between the two vectors [3, 0, 4] and [2, -1, 0];

                             [3, 0, 4] . [2, -1, 0] = | [3, 0, 4] | × | [Graphics:Images/index_gr_1.gif] |cosα


                                                     cosα =  [Graphics:Images/index_gr_2.gif]    
                                                       
                                                            α = [Graphics:Images/index_gr_3.gif][Graphics:Images/index_gr_4.gif]
                                                            
                                                                =  1 radian
                                                                
The angle between the line and the plane, θ is given by;


                            θ = [Graphics:Images/index_gr_5.gif]  -  1
                            
                               =    0.57 radians                                                

  
Note, if the value of α had been greater than one right angle, that is, the obtuse angle between the line and plane then, θ would be α -[Graphics:Images/index_gr_6.gif].
 

HOME