The Line of Intersection between two Planes

Problem: Find theline of intersection between the two planes given by the vector equations r1.[3, 4, 0] = 5 and r2.[1, 2, 3] = 6
A diagram of this is shown on the right.		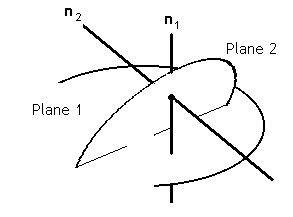is a normal vector to Plane 1 is a normal vector to Plane 2. By simple geometrical reasoning; the line of intersection is perpendicular to both normals.
To find the position vector, r, of any point on the line of intersection; find a vector, v, to which the line is parallel, find the position vector, a, of specific apoint on the line, then; r = a + tv, is the required result.	To find v; the cross product of two vectors gives a third vector which is perpendicular to both vectors. v is perpendicular to both and , therefore, v will beparallel to × , From the equations to the planes, .[3, 4, 0] = 5 and, .[1, 2, 3] = 6 = [3, 4, 0] and = [1, 2, 3] therefore × = [3, 4, 0] × [1, 2, 3] = = i - j + k = [12, -9, 9] 1. To find a; at any point on the line the position vector, , = let the point be (x, y, z), then; From the equations to the planes, (x, y, z) . [3, 4, 0] = 5 and (x, y, z) . [1, 2, 3] = 6 3x + 4y = 5 and x + 2y + 3z = 6 Let the point have an x co-ordinate = 0 then; y = and z = a is therefore [ 0, , ] 2. Substituting result 1. and 2. into r = a + tv gives; r = [ 0, , ] + t [12, -9, 9] or, more simply, r = [ 0, , ] + t [4, -3, 3] since the vector [12, -9, 9] is parallel to [4, -3, 3]

HOME

The Line of Intersection between two Planes

Problem:Find theline of intersection between the two planes given by the vector equations r1.[3, 4, 0] = 5 and r2.[1, 2, 3] = 6

Problem:

Find theline of intersection between the two planes given by the vector equations r1.[3, 4, 0] = 5 and r2.[1, 2, 3] = 6