In constructing the MoQ wimple model, I have attempted to build a model in the most simple terms the universe makes possible...in other words, using 4 points in space. Many years ago while most people my age were going to college, I happened to spend a whole lot of my time studying Buckminster Fuller's Synergetics 1 & 2 for reasons that weren't exactly clear, other than I could see value in it.
In Volumn 1 near the end, Fuller delved into what he called indigs. Indigs are integrated numbers created by adding any 2 or more digit numbers together until there is only one number left. In this way, Fuller shows that there are only 9 numbers, 1 through 9, and all other numbers are combinations of these numbers.
Zero is an invented symbol to facilitate mathematics. Before the invention of Zero, or the cypher, 9 was used to denote a plus-ness or minus-ness value- lessness. We can still do that by using a method called casting out nines to check sums of large numbers for correctness. By casting out nines and other numbers whos total is nine, the outcome of the problem is not effected in terms of value.
Using these clues, Fuller saw that an octave wave ran thru sequences of large numbers in this fashion...+1, +2, +3, +4, -4, -3, -2, -1. What this tells us is that there are only 4 'real' numbers in the universe. When I first read Lila, I could not help but be reminded of my long ago studies of Bucky Fullers work. In using indigs as the most fundamental four-ness of math as a starting point, I felt that constructing a model with them would perhaps show Pirsig's MoQ in real space.
Originally I wanted to develop this idea first, but when I began using my working MoQ wimple model, I suddenly was overwhelmed with the vastness of what it is I am dealing with. Therefore, I am attempting to scratch the surface first before proceeding, and have decided to construct a series of pages as jumping off points into the model.
This will be one such jumping point...the jump into Octave Wave models of MoQ. As my knowledge is at best fuzzy now with the passage of time, I am reaquainting myself with Fuller's work and will proceed with more construction as the ideas flow to me.
I am hopeful that by incorporating an Octave wave pattern into the MoQ wimple model, that we can show DQ as carrier waves with their internal-external valuelessness accomodating any wavelength or frequency, multiplying in respect to any convergent-divergent system (SQ) in the universe.
While that may sound easy for me to say, what it really means is, I hope by using the MoQ wimple model, we can explain quantum physics in everyday terminology that even a six year old can comprehend.

Yes, Yes, I know my artwork is terrible, but this is not an art page and I will hopefully be able to supply better graphics as my web skills increase. But this gives a good illustration of what I am attempting to do by introducing Fullerian math into the model. We are not examining the model itself here, but rather the underlying causal features that allow the universe to exist in the first place.
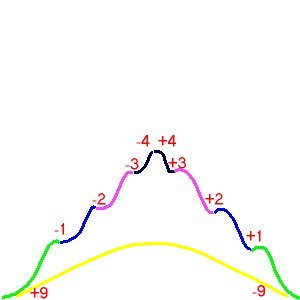
What I have tried to show is SQ in the model with the 9 indigs each assigned to a specific place within the underlying wave. Each Point is called a Chreode, or a canal in which Quality can manifest itself as SQ, which to our perception is real.
Underneath, I have placed a DQ wave with its value-lessness plus-ness and minus-ness assigned as well. This is a simple way of viewing a mathematical progression to infinity. It is a closed system by virtue, or by the nature of Quality itself.
When dealing with indigs, a distinct pattern emerges. Certain integers invariably produce discretely amplifying or diminishing alternative effects upon other integers. One produces a plus one-ness, two a plus two-ness, three a plus three-nes, four a plus four-ness, whereas it then reverses and a five produces a minus four-ness, six a minus three-ness, seven a minus two-ness and eight a minus one-ness.
Indig congruences demonstrate that nine is valueless and that the number system is inherently octave and corresponds to the four positive and four negative octants of the two polar domains (obverse and reverse) of the MoQ wimple model, and also govern the eight 45 degree angle constituent limits of 360 degree unity in the trigonometric function calculations.
Furthermore, the inherent +4, -4, 0, +4, -4, 0, +4, -4, 0 (and so on) of numbers also correspond (a) to the four varisized spheres integrating tritangentially to form the tetrahedron (the MoQ wimple model) and (b) to the octantation of the Coupler by its eight all-space filling mites which, being inherently plus-or-minus biased, though superficially invariant (i.e. are conformationally identical); altogether provide lucidly synergetic integration (at a kindergarten level) of cosmically basic number behavior, quantum mechanics, synergetics, nuclear physics, wave phenomena in general, and rational accoutability of experience in general.