Page Under  Construction

Introduction
My position in the working paper Internal Rate of Return Revisited⁽²⁾ differs from that in the Principles of Corporate Finance⁽³⁾ textbook by Richard A. Brealey and Stewart C. Myers.  Questions (polite challenges) have been posed the most times in a Brealey and Myers (B&M) context.  This paper addresses those questions, illustrated with spreadsheets from the Olin School of Business.⁽⁴⁾

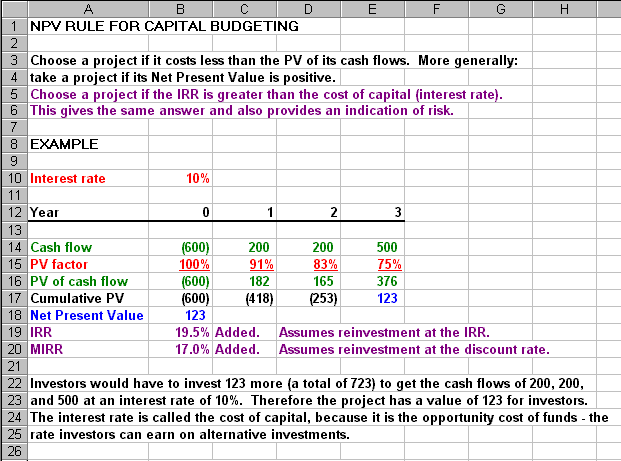
Net Present Value Rule
The NPV Rule is sound.  It is the value of a cash flow stream with the time value of money incorporated.  IRR (Internal Rate of Return) is equally sound and easily calculated.  The purple and teal markups are my additions to the spreadsheets.  The Excel IRR function assumes reinvestment at the IRR.  The MIRR (Modified IRR) function assumes reinvestment at the discount rate.

 .

Internal Rate of Return Rule
Three issues or problems are cited by the Olin School from B&M.   Commonly though, the first two and sometimes others are incorporated into a single demonstration.  This is unnecessarily confusing.  Separately they are understandable and manageable.

1. We usually keep track of lender or borrower outside the actual calculations.  Interest rate tables do not differentiate between them, but it is safe to assume the borrower will pay interest and the lender receive it.  Why should we expect more from discounting?
2. The first positive IRR is relevant.  The second is useful for identifying an upper limit for a meaningful discount rates and NPVs.   When IRR is incalculable as it sometimes is, NPV is suspect as well and may be nonsensical.
3. Larger projects should be expected to have higher NPVs.  IRR is useful with different sized projects, those with different economic lives and those that begin at other than the base year.  This difficulty is easily resolved by using incremental cash flows.

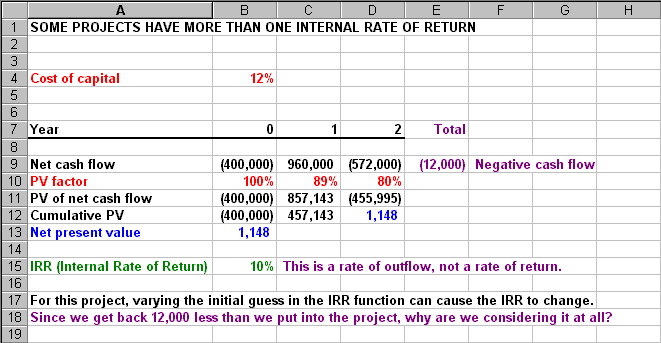
Multiple IRRs
Mixing borrower or lender with multiple rates of return is a common practice not limited to B&M.  It is unnecessarily confusing:

• Mixing obscures the fact that the 12 percent cost of capital is higher than the the relevant IRR.  The discount rate is in the nonsense zone where NPV increases with increasing discount rates. This implies increasing value with increasing cost.  It is absurd.
• Cash flows here are net negative, though the total is excluded.  No amount of rational discounting can make them positive.  If there is something to be analyzed here, it is for whomever cash flows are net positive--on the other side of the transaction.

Multiple IRR Plots
Column B reflects discount rates and NPVs as presented, plotted in the top graph.   The 12 percent discount rate is in a nonsense zone where NPV increases with it.  In this example, we should attempt to increase our cost of capital toward 19 percent, since doing so will increase NPV.

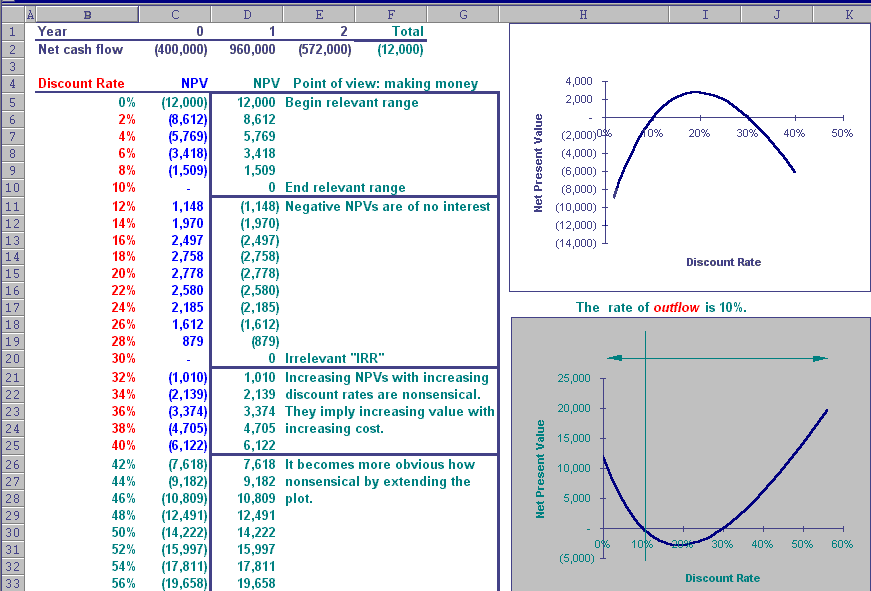
The rearranged bottom plot, viewed from the other side of the transaction, is less confusing.  The relevant range is defined by NPV at a zero discount rate to the relevant IRR where NPV is zero.  The 12 percent discount rate and other rates in the range 10-30 percent are of no interest or are nonsensical from this side of the transaction as well, since NPV is negative at all discount rates.  Beyond a 30 percent discount rate, we enter an extended nonsense zone where NPV continues to increase with the discount rate. The combined implications of both plots, are to increase shareholder wealth we should:

• maximize our cost of capital past 30 percent,
• look for projects with convoluted cash flows like this one, and
• figure out how to be on the side of the transaction where cash flows are net positive.

Incremental Cash Flows
Incremental NPV is recommended by B&M.  Incremental IRR is equally useful.  There is no NPV/IRR conflict.   IRR is calculable on public sector projects using incremental cash flows.

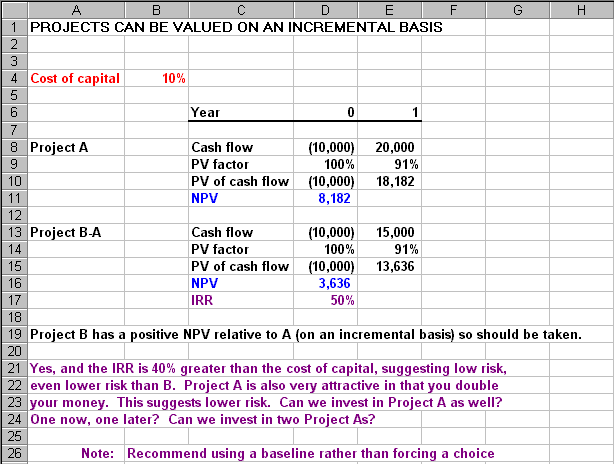
Mutually Exclusive Projects ⁽⁵⁾
Equal risk is assumed in "mutually exclusive (different sized)" projects, but ceteris paribus it is not.  Financial risk is higher with Project B, i.e., more money is at risk.  Further, larger projects usually have more tasks, more things to go wrong, than smaller ones.  Both projects are attractive, with the key tradeoffs between risk and return.  Risk is covered in another chapter in B&M, but risk and return are inseparable for decision making.

B&M are not necessarily "wrong."⁽⁶⁾  If you work at it sufficiently, you can construct a restrictive scenario where Project B is the only choice and is really best.⁽⁷⁾  This simply means that more money is better than less, even when discounted.  But focusing on this fact misdirects attention from other important considerations.   More realistic scenarios suggest several opportunities.  Two are:

• Execute one now, one later.  The sequence should probably be Project A first, then B.  In addition to having lower risk, Project A generates cash to finance the larger Project B.
• Execute Project A twice.  This normalizes Project A to Project B, with two Project As the better choice than one B.  Executing the same project twice or more should reduce risk since learning from the first execution is applicable to subsequent ones.⁽⁸⁾

Regardless, financial analysts should be able to accommodate any apparent contradictions rather than ignore them or dismiss IRR because it can be troublesome.  There are no contradictions between NPV and IRR in these examples.  Rather they highlight the need for both. The two measures complement each other.

Brealey & Myers Template
This B&M template is quite useful and available from the Olin School Corporate Finance Spreadsheets.  The template is more useful with the IRR and MIRR calculations.  If funds are to be reinvested at the IRR, use the IRR function.  If funds are to be reinvested at the cost of capital and not the IRR, then use the MIRR function.

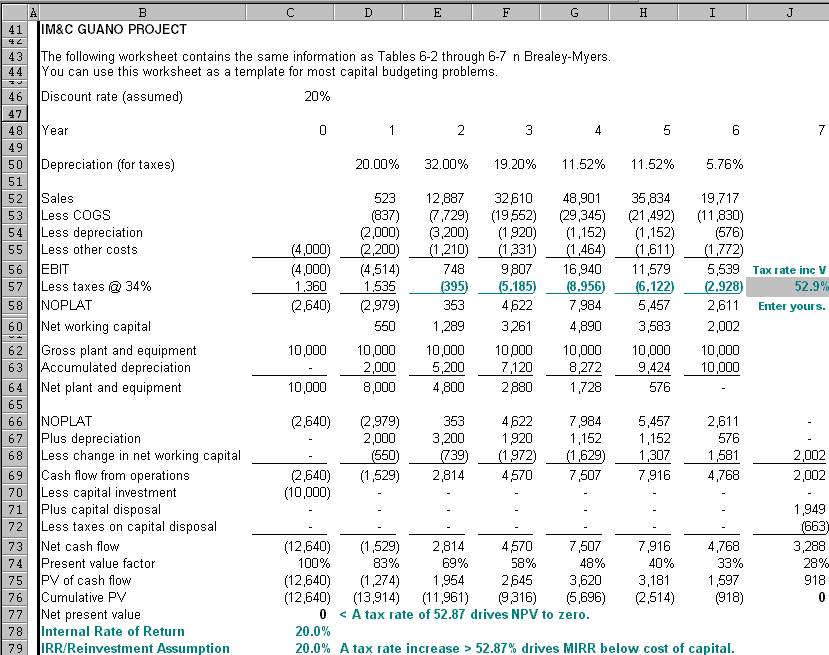
If the latter is the correct assumption, this may not be an attractive project.  At 24.3 percent (not shown), MIRR it is only 4.3 percent above the discount rate.  This suggests it is somewhat risky.  Even small changes in the cash flows, especially in early years, could drive IRR and MIRR below the discount rate and NPV negative.  For example, a tax rate increase from 34 percent to 52.9 percent starting in Year 2 drives NPV to 0 and IRR/MIRR to the discount rate.   The risk of a tax change is, for the most part, outside the control of the firm.

Conclusion
In my opinion Brealey and Myers:

• overemphasize NPV, while unnecessarily excluding IRR;
• overstate minor difficulties with IRR while ignoring the coexistent difficulties with NPV;
• assume unrealistically equivalent risk for different sized projects;
• overemphasize the easy-to-quantify aspects of capital budgeting decision-making;
• under emphasize the more difficult-to-quantify aspects, especially risk; and
• fail to prepare financial analysts for challenges that will invariably arise as a result.⁽⁹⁾

Notes

1. This working paper was done in Netscape Composer 4.0 for my use in responding to E-mail.  It uses a mix of fixed and proportional fonts plus font colors and styles. Other browsers may not present the way it was originated.  If you have trouble reading this page, contact me, Ray_Martin@AltaVista.net, and I will E-mail the graphics and text to you.  The most current versions of relevant papers and the Olin School of Business spreadsheets are available from the menu at URL:  https://members.tripod.com/~Ray_Martin/RMenu.html.
2. Internal Rate of Return Revisited at takes the position that NPV and IRR have essentially equivalent utility and that IRR is not inferior to NPV.
3. Richard. A. Brealey and Stewart C. Myers, Principles of Corporate Finance, 5th edition, Irwin-McGraw-Hill, 1996.  "Brealey and Myers" is used extensively in corporate finance.  It was in approximately the 3rd edition when I was introduced to it.  The authors present IRR as inferior to NPV for capital budgeting.
4. This paper is out of context and will be difficult to understand unless you are familiar with references 2. and 3 above.  The Excel spreadsheet screen captures are from Corporate Finance Spreadsheets, http://www.wuolin.wustl.edu/faculty/back/general.htm, at the Olin School of Business.  Using the Olin spreadsheets is for convenience in that address all the B&M questions posed to date.  None of the questions came from the Olin School of Business or any member of the faculty or student body.
5. Annual cash flows with and end-of-year discounting is a poor assumption in this problem for other than illustration.  Monthly cash flows would be more appropriate.  End-of-month discounting is appropriate if that is when cash is paid and received.
6. Questions are often posed in terms of right and wrong.  I prefer relevant and irrelevant (for the intended purpose).
7. Identical economic lives for greatly different sized (mutually exclusive) projects is another strained assumption.  Larger projects take longer and have more tasks, ceteris paribus.  The cumulative risk of more tasks is likewise greater.
8. "Learning curve" theory explains why, though it primarily applies to production.  Typically cost go down and schedules shorten on subsequent executions of a project as well.
9. Visualize a young financial analyst trying to explain the Multiple IRR problem above to a panel of senior decision makers.  A favorite sanity check at such reviews is to add the numbers.  This analysts is going to have to try to convince a senior group that a project in which they will receive $12,000 less than they invest is a smart thing to do because "NPV" at $1,184 is the largest one.  Fortunately such convoluted cash flows rarely, if ever, occur in practice.

1. 

   Access Since August 10, 1998: