Exercises in Differential Equations

Exercises in Differential Equations

Prove G_x(x⁺, x) = G_x(x, x^-) [Bir, p.54, l.-3].
Proof. G(x+e, x) = f(x)g(x+e)/p₀(x+e)W(x).
G(x, x-e) = f(x-e)g(x)/p₀(x-e)W(x).
G_x(x ⁺, x) = f(x)g'(x)/p₀(x)W(x) =G_x(x, x^-).

Prove [Go2, p.380, (9-8)].
Proof. [Fom, p.36, Remark 1 & Remark 2].

Prove the last equality of [Guo, p.147, (11)].
Hint. Use [Guo, p.22, (10)] and [Ru2, p.27, Theorem 1.34].

Prove the equality (i.e., the second expression for R'_k) in [Guo, p.163, l.6].
Hint. If f(s)®b and f '(s)®0 as s®a, then (fg)'(s)®bg'(a) as s®a. Let f(s)=p(s+b+k)csc p(b+s).

Prove (a). If n is not an integer, [sin (m+n)p]/[sin (m-n)p] ® -1 as m ® an integer.
          (b). If n is an integer, [sin (m+n)p]/[sin (m-n)p] ® +1 as m ® an integer [Hob, p.265, l.-8].
Proof. (a). e^(m+n)pi - e^-(m+n)pi = e^mpi (eⁿ^pi - e^-npi) if m is an integer.
           (b). Use l'Hôpital's rule.
Remark. From this exercise, one learns that one should be careful in applying l'Hôpital's rule.

Prove [Hob, p.196, (21)] by following the scheme described in [Hob, p.196, l.-5-p.197, l.9].
Remark. This exercise helps one understand the rules of phase assignment and how a transformation affects phases.

Prove that the expression in [Hob, p.265, l.7; there is a misprint in this expression: sin np in the numerator should be replaced by cos np] is zero.
Proof. Express sin and cos in terms of exponential functions.
Remark. sin (n-m)p is not necessarily equal to (-1)^msin np because m may not be an integer.

Prove the formula in [Guo, p.404, l.3-l.4].
Proof 1. Evaluate the contour integral òc {[cos (a-b)z-cos(a+b)z]/t²}dz, where C is the contour given by [Gon, p.703, Fig. 9.19].
Proof 2. cos (a-b)z-cos(a+b)z=(1-cos(a+b)z)-(1-cos (a-b)z). [Ant, p.243, (6.2.14] still holds if we replace P_n(z)eⁱlz (l>0) by 1-eⁱ^lz (the proof is similar to that of the original statement).
Remark. Jordan's Lemma [Gon, p.680, lemma 9.2] requires that l=a-b>0.

Prove S _nÎI e^inq=2pd(q) [Reic, p.294, l.13].
Proof. Use the Poisson summation formula [Zyg, vol. 1, p.68, (13.4)].

Prove all the statements in [Jack, p.34, l.13-l.19].
Hint. [Chou, p.60, Fig. 2.26] may help identify the inner side mentioned in [Jack, p.34, l.15].
Remark. This exercise tests if one understands the concept of solid angles thoroughly.

Prove the statement in [Chou, p.604, l.9].
Hint. d^m+2/dx^m+2 = (d²/dx²)(d^m/dx^m).

Prove [Jack, p.100, (3.26)].
Hint. Use induction and recurrence relations to prove [Guo, p.279, Exercise 8].

Prove that [Kre, p.63, (19.2)] is a general allowable representation of class r [Kre, p.63, l.-11].
Hint. Choose a 2x2 sub-matrix A of rank 2 from the Jacobian matrix [Kre, p.60, (17.1)]. Then A[du¹/dt, du²/dt]^t ¹ 0.

Suppose r << R. Prove that the length of the broken line in [Ken, p.28, Fig. 3.4 (ii)] is 2pR sinh (r/R).
Proof. In order to overcome the obstacle of imaginary angles, we use the Gaussian curvature (a more general concept) instead of the radius of curvature in our calculations.
C_N= 2pr[1-(1/6)(r/R)²+…] [Ken, p.28, l.-8]
= 2pr[1-(K/6)r²+…]
= 2pr[1+(|K|/6)r²+…] (K<0)
= 2p(-K)^-(1/2)[r(-K)^1/2+(1/6)(r(-K)^1/2)³+…]
= 2p(-K)^-(1/2)[exp (r(-K)^1/2) - exp (-r(-K)^1/2)]/2
= 2p(-K)^-(1/2) sinh (r(-K)^1/2).

Prove every statement in the following paragraph:
    On a sphere the sum of the angles of a geodesic triangle always exceed 180°, and may be as great as 900° . For small geodesic triangles on a sphere the angle sum exceeds 180° only slightly [Ber, p.61, l.-12-l.-9].
Proof. [Wea1, vol. 1, p.117, l.1-l.3].

Prove the second equality of [Jack, p.183, (5.45)].
Proof. Use [Guo, p.216, (4); p.239, (3)].

Prove [Jack, p.184, (5.47)].
Proof. Use [Guo, p.219, (6); p.239, (3)].

Prove [Chou, p.614, (IV.60)].
Proof. Use [Bir, p.256, (1'); p.259, l.3].

Prove
[Chou, p.618, (IV.85)].
[Chou, p.618, (IV.86)].
Proof. (A). Use [Guo, p.423, l.11] and then [Guo, p.349, (11)].
(B). Use [Barr, p.601, Corollary 1] and then [Chou, p.613, (IV.53) & (IV.54)].

Prove that the cross product transforms as a pseudovector [Jack, p.269, (6.147)].
Proof. [Jack, p.269, l.-16; Haw, p.197, l.2].

Prove [Matv, p.87, (10.1)].
Proof. [Lin76, p.181, l.15].

Prove the last two statements on [Matv, p.90].
Proof. A. Let f₁(x) = F₁(x-w₀); f₂(x) = F₂(x-w₀); f = f₁f₂; F(w)=f(w-w₀).
B. Use [Bor, p.126, l.6; p.128, l.-9; p.128, l.6].

(a). Verify [Hec, p.179, Fig. 5.45].
Solution. Read [Fin, §85] or prove [Tho, p.336, Remark 3].
(b). For each case in [Hec, p.180, Fig. 5.47], prove that a light source at one focus will form its image at the other focus.
Proof. (b). Read [Fin, §106] or the hint given in [Edw1, p.613, Problem 25].

Prove all the functions in [Coh, p.1470, (7), (8), (9), (10), and (11)] approach d(x) as e→0.
Proof. (ii). [Pat, p.494, (44)]; (iii). [Born, p.755, (3)]; (iv). [Born, p.758, (20) & (21)]; (v). [Lan3, p.152, l.-10].

Prove that [Morg, p.418, (A.4)] represents the evolute to the ellipse x²/n² + y²/(n²-1)² = 1.
Proof. [Mur, p.273].
Remark. This exercise teaches one how to find the coordinates of the center of curvature. It also gives one a hands-on feeling for the curvature of a plane curve [Mur, p.269, (2)]. [Mur, p.269, (2)] is a simple case of [O'N, p.69, Theorem 4.3]. Even though a case is simple and specific, one cannot conclude that it is not important and can be ignored. On the contrary, in physics applications, we use formulas for plane curves more often than those for space curves. It is a nuisance that every time we apply a formula for a plane curve, we have to derive it from the corresponding formula for a space curve. It is better to use the formulas for plane curves as the reference base and then treat the formulas for space curves as a natural generalization. In addition, it is easier to integrate the formulas for plane curves into a single set than those for space curves. Incidentally, this exercise reveals that modern textbooks on differential geometry emphasize new tools such as moving frames, but fail to give students hands-on experiences.

Prove [Fur, p.119, (2.171)].
Hint. (x+a)^-1-(y+a)^-1 = b
Þ y-x = b(x+a)(y+a) = b[(y+a)-(y-x)](y+a).

Show that the last integral in [Born, p.761, (6)] tends to zero as a®0.
Proof. dS' contains a factor a²; G contains a factor a^-1. Therefore, the integral contains a factor a. This factor a can be taken outside of the operator ¶/¶x.

Prove the second mean-value theorem for integrable functions [Jef, p.52, (5)].
Proof. Replace Hypothesis 1 in [Wid, p.163, Corollary 4.1], g(x) Î C, with "Let g(x) be a Lebesgue integrable function". The argument and conclusion of [Wid, p.163, Corollary 4.1] remain valid.
Remark. For the generalization from a specific point of view, we must keep our argument as specific as possible until the stage reaches the related specific viewpoint. The proof of this exercise is divided into four stages: [Wid, p.160, Theorem 2] ® [Wid, p.162, Theorem 3] ® [Wid, p.163, Theorem 4] ® [Wid, p.163, Corollary 4.1]. Our goal is to generalize the statements so that they will remain valid for integrable functions. Shall we generalize the first stage statement? The generalized theorem for integration by parts would be meaningless. Shall we generalize the second or third stage statement? It would be unnecessary for our purpose. Therefore, we generalize only the fourth stage statement. The fourth stage is the proper stage to weaken the related hypothesis.

Prove the equality given in [Born, p.754, (20)].
Proof. Change variables to eliminate the cross term:
ax²+bh²+2gxh
= x'h' (solve the quadratic equation)
= x"²+h"² (rotate the coordinate axes by p/4).
Use [Ru2, p.186, §8.27(1)] and then [Reif, p.607, (A.2.6)].

Prove [Born, p.107, (55b)].
Hint. Make cross products for both sides of [Born, p.107, (54)] with the unit normal of the plane of incidence. Substitute T₀ = T_|| + T_^ into the resulting equation. In order to calculate the cross products and properly use the law of cosines, it is better to have [Wangs, p.415, Fig. 25-12] at hand.

Prove the formula for the Gaussian curvature given in [Born, p.754, l.-4].
Proof. Use [O'N, p.212, Corollary 4.1; p.219, Exercise 2].
Remark. When one can find a reference in a modern textbook, one should not refer readers to very old ones unless they are very special. In [Born, p.754, l.-5], Born refers his readers to a textbook published in 1912, 68 years before [Born] was published. Perhaps it was a textbook that Born used during his college years. It may be a convenient reference for Born, but modern readers would have a hard time accessing it.

Prove the equality given in [Wea1, vol. 1, p.121, l.9-l.10].
Proof. Do not use the identities given in [Wea1, vol.1, p.121, l.3-l.5] until you read [Wea1, vol. 1, p.121, l.11].
Eu'[(d/ds)(Vu')]=Vu'Eu"+Eu'²(V₂v').
2Eu"= -E₁u'²-2E₂u'v'+G₁v'²   [Wea1, vol. 1, p.100, (3)].

Prove the equalities given in [Wea1, vol. 1, p.119, l.-11].
Proof 1. cos w = F/(E^1/2G^1/2) = F/(H²).
H²= EG - F² = H⁴-F².
Proof 2. du = 0
Þ ds = G^1/2 dv [Wea1, vol. 1, p.55, l.18]
Þ sin w = [H/(E^1/2)] G^-1/2     [Wea1, vol. 1, p.56, (7)]
= H^-1.
Proof 3. The geodesic distance u in [Wea1, vol. 1, p.119, Fig. 18] can be regarded as du.
Draw a curve PQ parallel to v=0. The curve PQ intersects u=0 at Q.
Then the arc length of PQ equals E^1/2 du.
By definition, sin (p-w) = du/(E^1/2 du).

Prove that the indicatrix at any point of a central quadric is similar and similarly situated to the parallel central section [Wea1, vol. 1, p.130, l.19-l.21].
Proof. The elliptical intersections of parallel planes with an ellipsoid are similar (Substitute z=px+qy+r [where r is a parameter] into [Wea1, vol. 1, p.124, (1)]). Then use the statement given in [Wea1, vol. 1, p.75, l.4-l.7].

Prove the equality given in [Wea1, vol. II, p.64, l.16].
Proof. Let r₂´r₃ = ar₁+br₂+cr₃.

Prove the equality given in [Sne, p.74, (8)].
Proof. (z²-a²x²)^1/2 = ay+b Þ zdz = a²xdx + (z²-a²x²)^1/2 ady.
dp/(-q²) = dq/(pq) Þ (p²+q²)=a² Þ pz = a²x Þ q² = a²-a⁴x²/z².
Remark. Because the answer is given, we know what p and q would look like. The question and the answer are like a container with a piston at each end. When we squeeze toward the middle from the two ends, the method for obtaining the solution is inescapable.

Prove that d_j in [Dug, p. 298, Ex. 2] is totally bounded.
Proof. Find two balls, one containing -¥ and the other containing +¥. The complement of the union of the above two balls is compact.

Prove the two statements in [Dug, p.325, Ex. 8].
Proof. (a). Drag vertical lines (1/n)´I down to 0. Then drag the horizontal line I´0 leftward to 0.
(b). The line segment 0´I cannot stay intact as the nearby vertical lines (1/n)´I are dragged down to 0.

Let B and C be two bases of a vector space. Then Card (B) = Card (C).
Proof. [Leu, p.25, Theorem 2.9 & p.34, Theorem 3.3].

Prove [Mun00, p.498, Corollary 82.2].
Proof. Þ: [Mun00, p.486, Lemma 80.4].
Ü: [Mun00, p.495, Theorem 82.1; p.346, Theorem 54.6(a)].

Show that the topology of (St¯ x)´I is coherent with the subspaces A_a´I [Mun00, p.504, l.-9-l.-8].
Proof. St¯ x is the largest topology for which p|_{A_a}: A_a® St¯ x is continuous
Û St¯ x is the largest topology for which p: È_aA_a® St¯ x is continuous (È_a refers to the free union [Dug, p.127, l.-10])
Û p: È_aA_a® St¯ x is a quotient map [Dug, p.121, Proposition 1.2]
Þ p´i_I : (È_aA_a)´I ® (St¯ x)´I is a quotient map [Mun00, p.186, Exercise 11]
Û (St¯ x)´I is the largest topology for which p´i_I : (È_aA_a)´I ® (St¯ x)´I is continuous
Û (St¯ x)´I is the largest topology for which p|_{A_a}´i_I : A_a´I ® (St¯ x)´I is continuous.

[Spi, vol. 1, p.473, Exercise 9].
Proof. Write the equality given in [Spi, vol. 1, p.473, l.2] in the matrix form: [g'_ab]=U[g_ij]V. Take their inverses and then transpose both sides.
Remark. This exercise enables us to prove [Kre, p.108, Definition 31.2] as a theorem using [Kre, p.108, Definition 31.1] if det (g_ij) ¹ 0. This nonsingular case can be used as a model that motivates us to define the general case given in [Kre, p.108, Definition 31.2].

Construct a continuous and surjective map f: S¹ ® V² [Dug, p.344, l.20-l.21].
Solution. Let f satisfy f [0, 1/2] = V²[Dug, p.105, Theorem 4.4]. Let f [1/2, 1] be the line segment from f(1/2) to f(0).

Solve the Schoenflies problem for n=1.
Solution. [Dug, p.363, l.16-l.20] & [Ru2, p.302, Theorem 14.8; p.310, Theorem 14.9; p.311, l.7-l.8]. However, [Ru2] does not provide a proof for the statement given in [Ru2, p.311, l.7-l.8]. We can use [Dug, p.356, Theorem 1.2 (4)] to prove this unproven statement: Fix a point x on the Jordan curve J; choose a small neighborhood V of x and a point y which belongs to V and the bounded component; draw a line segment L from x to y; choose z Î L-{x} before L intersects J twice.

(The number of integration constants; the number of parameters of integral curves)
Prove the statement given in [Cou, vol. 2, p.2, l.-14-l.-11] and the statement given in [Born, p.720, l.-8-l.-6].
Proof. [Bir, p.143, l.-6; Spi, vol. 1, p.199, Theorem 4; Arn1, p.305, Corollary 2].
Remark. Both "integration constants" and "parameters" refer to initial conditions. [Spi, vol. 1, p.199, Theorem 4; Arn1, p.305, Corollary 2] specify the domain of the initial conditions.

There exists a set of m linearly independent "generalized" eigenvectors of B [Was, p. 19, l.-4-l.-3].
Proof. [Jaco, vol. II, p.70, Theorem 3].

Prove the existence of a polynomial n(l) ¹ 0 of degree < kq such that en(A) = 0 [Jaco, vol. II, p.71, l.12-l.13].
Proof. Express f_i as eg_i(A).

For Jordan normal form, each numeral "1" in [Jaco, vol. II, p.95, the second matrix] and [Har, p.59, (5.15)] is below the diagonal, while each numeral "1" in [Her, p.301, Definition] and [Cod, p.63, matrix J_i] is above the diagonal. Explain why the definitions of the same form have different appearances.
Explanation 1. Let T be a linear transformation on a vector space. Suppose T is represented by matrix A if we use a row vector to represent a vector. Then the same transformation T will be represented by the transpose A^t of A if we use a column vector to represent a vector [Her, p.298, l.1-l.2].
Explanation 2. Someone may argue with me by pointing out that both [Her, p.298, l.1-l.2] and [Jaco, vol. II, p.37, (9)] use row vectors, but [Her, p.294, Theorem 6.5.1] and [Jaco, vol. II, p.99, Exercise 2] still have different appearances. Let us examine their proofs. The proof of [Her, p.295, Lemma 6.5.4] uses reduction to absurdity which involves a long argument in order to reach a contradiction. Herstein calls his argument sticky [Her, p.294, l.-1]. I call it ineffective. If one puts Herstein's argument into practice, one will find it is essentially based on trial and error. The following proof of [Jaco, vol. II, p.99, Exercise 2] is more effective, methodical and systematic.
Proof. Let m(l) be the minimum polynomial of (a). Then m(l) | l^k.
By [Jaco, vol. II, p.92, l.-10-p.93, l.8; p.98, l.-11], d_q=m(l).
Then "j£q, d_j has the form l^m (m£k).
By [Jaco, vol. II, p.72, (9) & (10)], we complete the proof.
    In my opinion, an effective proof preserves the order, while an ineffective proof destroys the order. Furthermore, if we compare the proof of [Her, p.294, Theorem 6.5.1] with that of [Jaco, vol. II, p.99, Exercise 2], we notice that the former proof does not use complicated theorems such as [Jaco, vol. II, p.70, Theorem 3]. However, this advantage does not necessarily make the former proof a more effective approach. Unless we measure our progress according to effectiveness, we may spend our effort only to fall back or circle around rather than advance.¬¬¬

Prove the statement given in [Har, p.85, l.-8-l.-6].
Proof. Þ: [Har, p.73, Corollary 11.1; p.59, (5.18)].
Ü : By choosing a proper basis, the matrix of any linear transformation can be expressed as a Jordan normal form. For the same l(j), k can be restricted to 0£k£h(j) because {t^l(j)(log t)^k | k assumes more than h(j) values} must be linearly dependent.

There is a 2-family of characteristic curves in xyz-space for the system [Joh, p.9, (4.3)]. (see [Joh, p.10, l.2-l.3])
Proof. The intersection of the two surfaces given in [Sne, p.51, (5)] is a characteristic curve. c₁ and c₂ are two parameters.

(a). Prove the equality in [Inc1, p.121, l.4].
(b). D_i/D_i-1 = log* (v₁, …, v_i) [Inc1, p.121, l.8].
Proof. (a). u₁, …, and u_n satisfy [Inc1, p.121, l.4]. Consequently, so does u.
(b). By [Inc1, p.120, l.4; p.121, l.4], (D_r-1/D_r)(D_r-1/D_r-2) = v_r^-1.
Let x_r = D_r/D_r-1.
Then x_r-1/x_r = v_r^-1, i.e., x_r = v_r x_r-1. Let x₀ =1.

Let P and Q be given as in [Inc1, p.131, l.11-l.12]. Then
(a). PQ º QP º D³- 5x^-2D³+ 15x^-3D²- 30x^-4D + 30x^-5.
(b). P³ º Q² º D⁶ - 6x^-2D⁴ + 24x^-3D³ - 72x^-4D² + 144x^-5D - 144x^-6.
Remark. [Inc1, p.131, l.l.14] fails to give the expansion of the product as in (b) above. Since the product of two differential operators is not commutative, their product usually produces many more terms than the product of two polynomials even though a differential operator can be represented in polynomial form. Thus, we must constantly fight against the strong inclination to cause errors. It is easy for us to find where we made a mistake if the expansion of the product is given. Otherwise, one will not know what to do if one unfortunately finds that P³ does not equal Q² in one's calculation.¬

(a). Prove [Ahl, p.186, (6)].
(b). If n_n > log M_n, then lim_n®¥ M_n^1/n_{^{_{^_n}}} /|b_n| = 0 [Ahl, p.186, l.15].
Proof. (a). P_n((z-b)^-1) - p_n(z) can be considered the last term of the right-hand side of [Ahl, p.125, (28)], where f_n(z) can be calculated by [Ahl, p.126, (29)].
(b). log M_n <n_n Þ M_n^1/n_{^{_{^_n}}} <e.¬

(a) Prove Sin (iK', l) = i [Gon1, p.416, l.6].
(b). Prove Tan (iK'/2) = i Tan (K/2) [Gon1, p.418, (5.15-17)].
Proof. (a). Cos (iz, l) = Cos (z, -l) [Gon1, p.412, l.-11].
Tan (iz, l) = i Tan (z, -l) [Gon1, p.403, (5.10-1)].
K'_-l = K_l [1].

Prove cn z = cos (am z) [Gon1, p.428, l.-6].
Proof. By [Gon1, p.428, (5.17-16)], -(p/2) £ f £ p/2.
Consequently, cos f ³ 0.
By [Gon1, p.428, l.9; Fig. 5.20], -K £ x £ K.
By [Gon1, p.388, Fig. 5.6], çTan x÷ £ 1.

Prove f (-1/2 - t/2) = 0 [Guo, p.506, l.-9].
Proof. Use [Guo, p.501, (4)] to prove J₄'(-1/2 - t/2)/J₄'(-1/2 - t/2) = ip.
Use [Guo, p.501, (4)] to prove J₁'(-1/2 - t/2)/J₁'(-1/2 - t/2) = ip.

Prove w(e₁ - e₃)^1/2 = K [Guo, p.513, l.4].
Proof. x = e₁ Þ t = 1 [Guo, p.513, (15)]
Þ v = 1/2 [Guo, p.510, (1)]
Þ u = pJ₃² /2 [Guo, p.510, (1)]
= K [Guo, p.511, (6)].
w = z [Gon1, p.451, l.6]
= K (e₁ - e₃)^-1/2 [Guo, p.513, (15)].
Remark. [Guo, pp.526-527, Exercise 9.10] uses transformations which involve many unnecessary calculations. Using Guo's method, we have to consider the sign problem when taking square roots [Guo, p.527, l.6]. There is a way to avoid these troubles. In my opinion, only in [Gon1, §5.28] do we need to use various transformations. Then we treat various formulas in [Gon1, §5.28] as standard results. If we want to establish a relationship between two quantities, it is enough to use basic relationships [Guo, p.510, (1); p.513, (15)]. It is absolutely unnecessary to use the transformations again.

Prove [Guo, p.512, (12)].
Proof. Use [Gon, p.543, (8.4-10)].

Prove csc² z = å^¥_{n
= 0} a_2n z²ⁿ (|z| p), where a_2n = 2p^-²⁽ⁿ⁺¹⁾(2n+1)å^¥_{m =1} m ^-2n-2 [Wat1, p.438, l.-14-l.-12].
Proof. (z-mp)^-1= (-mp)^-1(1 + (z/mp) + (z/mp)² + …)
Consider (z-mp)^-2+ (z+mp)^-2.
Remark. At first, I did not know how to begin to solve this problem, so I went to a library and browsed [Gon1, chap. 4]. As soon as the equalities given in [Gon1, p.289, l.2-l.3] caught my attention, I knew I could solve this problem.

[Gon, p.721, l.3-l.4] Prove that (f(s) = O(|s|^{- a}), a>0, as |s| = R®¥) implies [Gon, p.721, (9.11-60)].
Proof. Use x = 0 to divide G⁺ [Gon, p.720, Fig. 9.24] into four pieces:
G⁺ = Lu È Ll È T È B, where Lu is the upper half of the left piece, Ll is the lower half of the left piece, T is the top piece and B is the bottom piece.
I. Let b(R) = arc sin (c/R). Then
|ò_Te^stf(s)ds| £ e^ctR^-a (R b(R)) ® e^ct ×0×c = 0 as R®¥.
Similarly, |ò_Be^stf(s)ds| ® 0 as R®¥.
II. ò_Lue^stf(s)ds = ò_[p/2,p]exp(Re^iqt)f(Re^iq)Rie^iqdq
= ò_[0,
p/2]Re^i(q+p/2)tf(Re^i(q+p/2))Rie^i(q+p/2)dq.
|ò_Lue^stf(s)ds| £ ò_[0,
p/2]|exp(Re^i(q+p/2)t) f(Re^i(q+p/2)) Rie^i(q+p/2)|dq
£ ò_[0,
p/2]e^{-(Rsin
q}^)tR^-aRdq £ ò_[0,
p/2]e^-(R2q/p^)tR^-aRdq
= (p/2)(1-e^-Rt)R^-a® 0 as R®¥.
III. For Ll, first change qÎ[-p, -p/2] to q₁ = - q Î[p/2, p], and then change q₁ Î[p/2, p] to q₂ = q₁ - p/2Î[0, p/2]. Then the argument for Ll can proceed similarly to that for Lu.¬

Prove [Guo, p.514, (1)].
Proof. The proof given in [Guo, p.514, l.-6-l.-2] is incorrect.
[Guo, p.509, (12)] should have been corrected as D^1/4 = e(v|t)[pJ₁'²/(4w³)], where e(v|t)⁴ = 1.
The transformation t®t' changes e₁, e₂, and e₃ to e₃, e₂, and e₁ respectively. Thereby, the transformation leaves D invariant. Then we have J'₁(0|t')/w'^3/2 = e₁(t) [J'₁(0|t)/w^3/2], where e₁(t)⁸ = 1.
Since J'₁(0|t'), J'₁(0|t), and t^3/2 are non-zero analytic functions in Im t > 0 [Guo, p.507, (3); p.502, l.10-l.13; Wat1, p.463, l.10-l.21], e₁(t) is continuous in Im t > 0.
Consequently, e₁(t) is a constant e₁. Let t = t' = i. Then e₁ = i^-3/2.
Remark. The proof of the formula in [Wat1, p.475, l.11] uses the Liouville theorem [Wat1, p.431, l.-8-l.-7]. In contrast, the proof of [Guo, p.534, (2)] allows us to avoid using the complicated Liouville theorem.

Let k be defined as in [Wat1, p.478, l.22] and k' be defined as [Wat1, p.479, l.8].
If 0 < k < 1, then 0 < k' < 1 [Wat1, p.501, l.20].
Proof. By [Sak1, p.399, Theorem 12.11], t must lie on ¶G₀" [Sak1, p.399, l.16-l.17].
By [Wat1, p.484, l.5-l.6], t cannot lie on x = 1.
By [Wat1, p.483, l.9-l.10], t cannot lie on the semicircle OBC1 [Wat1, p.482, Figure].
Consequently, t = ai, where a > 1.

(a). If the series u₀(x)+u₁(x)+… converges uniformly and if the sequence {v_n} is of bounded variation, then the series u₀(x)v₀(x)+u₁(x)v₁(x)+… converges uniformly [Zyg, vol.1, p.4, Theorem 2.4].
(b). Suppose the sequence {v_n} is non-negative, non-increasing and of bounded variation.
If v_n ® 0, then v₀-v₁+v₁-v₂+… = v₀.
Proof.
(a). (The first proof)
(S_1£n£nu_nv_n) - U_nv_n = S_1£n£n-1U_n(v_n-v_n+1) [Zyg, vol.1, p.3, (2.1)].
Then take lim sup _n |   | on both sides.
(The secnd proof)
{v_n} is of bounded variation
Þ {v_n} converges [ Zyg, vol.1, p.4, l.10]
Þ {v_n} is bounded
There exists an M > 0 such that |v_n| £ M.
|S_m£n£nu_nv_n| £ |S_m£n£nu_n| M £ e.
(b). |v₀-v₁| + |v₁-v₂| +…+ |v_n_-1-v_n| = v₀-v_n.
Remark. For (b), we tend to use the equality (v₀-v₁)+(v₁-v₂)+… = v₀+(-v₁+v₁)+(-v₂+v₂)….
The example v_n = S_1£n£n2^-n shows that the above equality is incorrect.
The example v_n = 1+ n^-1 shows that the hypothesis v_n ® 0 cannot be omitted.

If f(x+h) + f(x-h) - 2f(x) = O(h^a), 0 < a < 1, then f Î L_a [Zyg, vol.1, p.44, l.-2].
Proof. |f(x+t) + f(x) - 2f(x+(t/2))| £ At^a.
Let 0 < h^a £ g/2.
Find a nonnegative integer n such that 2ⁿh^a Î [g/2,g].
Let g(t) = f(x + t) - f(x).
Then |g(t/2ⁿ^-1) - 2 g(t/2ⁿ)| £ A (t/2^n-1)^a.
1+2^1-a+2^{2 (1-a)}+…+2^{(n-1) (1-a)} = [2^{n (1-a)} -1]/(2¹^-a-1).
|g(t) - 2ⁿg(t/2ⁿ)| £ [A/(2¹^-a-1)] 2^{n
(1-a)} t^a = A₁2ⁿh^a (let t = 2ⁿh).
|g(h)| £ (2M)/(2ⁿ) + A₁h^a £ (2M h^a)/(g/2) + A₁h^a.
Remark. In [Zyg, vol.1, p.44, l.-1], Zygmund says that the proof of this exercise is the same as the proof of [Zyg, vol.1, p.44, Theorem 3.4]. In fact, the two proofs are not exactly the same. The proof of this exercise requires a minor modification of the proof of [Zyg, vol.1, p.44, Theorem 3.4].

Prove the statement given in [Zyg, vol.1, p.56, l.17-l.18].
Proof. ò_{[T, +¥)} (sin (n+w)t)/t dt
= ò_{[(n+w)T, +¥)} (sin t)/t dt = [cos (n+w)T]/[(n+w)T] - ò_{[(n+w)T, +¥)} (cos t)/[(n+w)t²] dt.
ò_{[(n+w)T, +¥)} (cos t)/[(n+w)t²] dt
= [-sin (n+w)T]/[(n+w)³T²] + ò_{[(n+w)T, +¥)} (2 sin t)/[(n+w) t³] dt.
| ò_{[(n+w)T, +¥)} (sin t)/[(n+w) t³] dt | £ (n+w)^-3 T^-2.
Remark. In this exercise we have to use integration by parts twice. If we use integration by parts only once, our error estimate will not be precise enough to meet the requirement.

Prove that I₂ = o(1) uniformly in every interval where f is bounded [Zyg, vol.1, p.62, l.-7].
Proof. Suppose that m(E) is small.
ò_E |f(x+t)| = ò_E-x |f(t)|.
ò_E |f(x-t)| = ò_x-E |f(t)|.
ò_E |f(x)| = m(E) ´ |f(x)|.

Prove the analogue of [Zyg, vol.1, p.62, Theorem 10.1] for conjugate series [Zyg, vol.1, p.66, l.1].
Proof. Let h = p(2n)^-1.
I₃ = ò_{[ 0, h]} y(t) [2^-1cot (t/2)] cos nt dt = -ò_{[
-h/2, h/2]} y(t+2^-1h) {2^-1cot [2^-1(t+2^-1h)]} sin nt dt.
(sin nt){2^-1 sin [2^-1(t+2^-1h)]}^-1 » nt [4^-1(t+2^-1h)]^-1 £ 5n for tÎ[-h/2, h/2] if n is large.
|I₃| £ 5n ò_{[
-h/2, h/2]} |y(t+2^-1h)| dt = 5n ò_{[ 0, h]} |y(t)| dt if n is large.
I₄ = ò_{[
-h, h]} y(t+h) {2^-1cot [2^-1(t+h)]} cos nt dt
= ò_{[ 0, h]} y(t) [2^-1cot (t/2)] cos n(t-h) dt
= ò_{[ 0, h]} y(t) [2^-1cot (t/2)] sin nt dt.
|I₄| £ n ò_{[ 0,
2h]} |y(t)| dt.
Remark. Lebesgue's test can be said the pinacle of Fourier analysis because it still ensures the convergence of a Fourier series even though Lebesgue weakens the hypothesis to the utmost. If one can do this exercise by oneself, one will gain a deep understanding of the behavior of the integral ò_E as m(E) ® 0. Up to now we still understand very little about this area.

Prove
(a). The fact that the first term of [Zyg, vol.1, p.52, (6.2)] is finite implies [Zyg, vol.1, p.65, (11.6)].
(b). The fact of the second term of [Zyg, vol.1, p.52, (6.2)] is finite implies [Zyg, vol.1, p.66, (11.7)].
Proof. (a). Using [Roy, p.70, Problem 23.d; p. 72, Problem 31], we may assume that f is continuous.
ò_{[h, p]} |f(t+h)| t^-1 dt = ò_{[h, p]} |f(t+h)| (t+h)^-1(t+h) t^-1 dt
£ 2 ò_{[h, p]} |f(t+h)| (t+h)^-1 dt = 2 ò_[2h,p+h] |f(t)| t^-1 dt
£ 2 ò_{[0,
2p]} |f(t)| t^-1 dt.
Remark. This exercise is an example of the following problem:
Suppose f (x, y) exists as y®0 for each fixed x in the neighborhood of 0. How do we impose a weak condition on f so that f (x, x) exists as x®0?
[Kap, p.267, Theorem] is another example.¬

Prove that if g(x) tends to 0 monotonically in the neighborhoods of +¥ and of -¥, then g* defined as in [Zyg, vol.1, p.69, l.2] is absolutely integrable over (-¥, +¥).
Proof. Let k be a nonnegative integer and A = (2p)^-1 ò_{[2kp, 2(k+1)p]} g(t)dt.
ò_{[2kp, 2(k+1)p]} |g(t)| dt = ò_{[2kp, 2(k+1)p]} |g(t)-A| dt
= ò_{[2kp, 2(k+1)p]Ç{x:g(x)³A}} (g(t)-A) dt + ò_{[2kp, 2(k+1)p]Ç{x:g(x)<A}} (A-g(t)) dt
£ 2p[g(2kp) - g(2(k+1)p)].

Prove that if we omit the term x^a-1 in [Zyg, vol.1, p.69, (13.8)], the limit will exist uniformly in 0£x£2p [Zyg, vol.1, p.70, l.4-l.5].
Proof. If we rescale by substituting 1 for 2p, then we only need to prove that
x^a-1+…+ (x+n)^a-1- a^-¹n^a converges uniformly in [0, 1].
Let m > n, A = (n+2)^a-1+…+ (m+1)^a-1- a^-¹m^a+ a^-¹n^a,
and B = (n+1)^a-1+…+ m^a-1- a^-¹m^a+ a^-¹n^a.
Then A £ (x+n+1)^a-1+…+ (x+m)^a-1- a^-¹m^a+ a^-¹n^a £ B in [0, 1].
|B| £ a^-¹m^a - a^-¹n^a - [(n+1)^a-1+…+ m^a-1] £ n^a-1- m^a-1.
|A-B| £ (n+1)^a-1+ (m+1)^a-1.
Let m, n ® +¥.

Prove that, with an error uniformly O(1), the periodic function Y_a(x) is 0 for -p£ x < 0
and is 2px^a-1/G(a) for 0 < x £ p.
Proof. For xÎ[-p,p]\{0},
G(x) = lim _n®¥ (Sⁿ_k=0 g(x+2kp) - (2p)^-1ò_{[-2np,
2np]}g(t)dt) [Zyg, vol.1, p.69, (13.6)]
= g(x) + lim _n®¥ (Sⁿ_k=1 g(x+2kp) - (2p)^-1ò_{[-2np,
2np]}g(t)dt)
= g(x) + O(1) [Zyg, vol.1, p.70, l.4-l.5].

Prove [Zyg, vol.1, p.92, (3.24)].
Proof. òòdtdw = òòdwdt because the integral given in [Zyg, vol.1, p.55, (7.2)] converges uniformly [Zyg, vol.1, p.56, l.-10] in wÎ[0,w₀], where is w₀ finite, except in the neighborhood of integral vales of w [Zyg, vol.1, p.56, l.-14].
We may assume that w is not an integer.
ò_[0,w]S_n£_t A_n(x) dt = A₀(x)+S_n=0¹A_n(x)+…+S_n=0^[w]-1A_n(x)+(w-[w])S_n=0^[w]A_n(x)
= S_n£_[w]-1 ([w]-n) A_n(x)+(w-[w])S_n=0^[w]A_n(x)
= S_n£_[w]-1 (w-n) A_n(x)+(w-[w])A_[w](x)
= S_n£_[w] (w-n) A_n(x).

Let f have a period of 2p and let f be integrable on [0, 2p]. Prove [Zyg, vol.1, p.92, (3.24)].
Proof. ò_{[0,
+¥)}|f(x+t)| sin²(wt/2) (wt²)^-1 dt
= ò_{[0, 2p)}|f(x+t)| sin²(wt/2) (wt²)^-1 dt + ò_{[2p,
+¥)}|f(x+t)| sin²(wt/2) (wt²)^-1 dt
£ Mò_{[0, 2p)}|f(x+t)| dt + w^-¹(2p)^-2ò_{[0,
2p]} |f| (1^-1+2^-1+3^-1+…) dt.

S_n_=n+1^¥ A_n^a-¹e^-int = A_n+1^a-1e^-i(n+1)t/[1-e^-it] + S_n_=n+1^¥ A_n+1^a-2 e^-i(n+1)t/[1-e^-it] [Zyg, vol.1, p.95, l.-4].
Proof. It suffices to prove that
S_n_=n+1^¥ A_n^a-¹e^-int = A_n+1^a-1 S_n_=n+1^¥ e^-int + S_l_=n+1^¥ A_l+1^a-2 S_m_=l+1^¥ e^-imt.
The convergence of the first series is proved in [Zyg, vol.1, p.94, l.-4]. We may use [Zyg, vol.1, p.77, (1.16)] and [Ru1, p.65, Theorem 3.50] to prove the convergence of the the third series of the intermediate equality. All need to do is compare the coefficients of e^-int on both sides of the equality. Using [Zyg, vol.1, p.77, (1.12) (i)] and mathematical induction, we can prove
A_n+1^a-1 + A_n+2^a-2+…+A_n^a-² = A_n^a-¹ if n ³ n+2.
Remark. It is unnecessary to use the method of summation by parts to prove the above identity [Zyg, vol.1, p.95, l.-6].

Prove that [Zyg, vol.1, p.100, (7.3)] is {¶F(r,x)/¶x}_{x = x₀}.
Proof. By [Zyg, vol.1, p.45, Theorem 4.4], the series F(r, x) converges uniformly in x as the number of its terms approaches +¥.
Then we use [Ru1, p.135, Theorem 7.11].
Remark. We are inclined to use [Ru1, p.140, Theorem 7.17] instead because it discusses differentiation. However, it would be incorrect if we try to prove this exercise using [Ru1, p.140, Theorem 7.17]. This is because one of the hypotheses of [Ru1, p.140, Theorem 7.17] may not be satisfied. That is, f_n' may not converge uniformly in x.

Prove f* = f^~ [Zyg, vol.1, p.121, l.14].
Proof. There is a gap in Zygmund's proof. In addition, his argument does not seem to proceed in the right direction. If we can prove f_n^~(x) ® f^~(x) for every xÎ[0, 2π], the gap will be filled and the proof of [Zyg, vol.1, p.121, (13.28)] will be completed.
By [Zyg, vol.1, p.121, l.12], f is analytic.
y_n,
x(t) - y_x(t) has no constant term, so |y_n,
x(t) - y_x(t)|/|2 tan (t/2)| is bounded on [0, 2π].
y_n,
x(t)- y_x(t) ® 0 for every tÎ[0, 2π] as n®¥.
By [Ru2, p.27, Theorem 1.34], -π^-1ò₀^π |y_n,
x(t) - y_x(t)|/|2 tan (t/2)| dt ® 0 as n®¥.

Find a function fÎL₁ such that f^~ÏL₁ [Zyg, vol.1, p.121, l.-7].
Solution. Let f '(x) = S₂^¥ (sin nx)/(n log n).
Then S^~[f '] = S₂^¥ (cos nx)/(n log n), where the right-hand side is an unbounded function [Zyg, vol.1, p.253, l.-5].
S[(f^~)'] = S[(f ')^~] (since (f^~)' = (f ')^~ [Zyg, vol.1, p.51, (5.7)])
= S^~ [f '] [Zyg, vol.1, p.253, l.-1].

Prove [Zyg, vol.2, p.242, (1.5)].
Proof. Use [Zyg, vol.1, p.55, (7.1)(i)].
sin [w]t - sin w't = 2 cos [2^-1([w]+w')t] sin [2^-1([w]-w')t] = 2 cos [([w]+4^-1)t] sin (-t/4).
p^-¹ò_[_-_d_,d] f(x+t)[(sin [w]t - sin w't)/t]dt
=2p^-¹ò_[_-d_,d] f(x+t)[t^-1 sin (-t/4)] cos [([w]+4^-1)t] dt
®0 [Zyg, vol.1, p.46, (4.6)].
Remark. By [Zyg, vol.1, p.46, (4.6)], o(1) in [Zyg, vol.2, p.242, (1.5)] is uniform in x₀.¬

Prove that (1.9) tends uniformly to 0 for x₀ÎJ_a' [Zyg, vol.2, p.244, l.7-l.8].
Proof. I. Case x₀ ³ 0.
ò_[B,B'] (f(t)t^-1)[t(t-x₀)^-1] sin (t-x₀) dt
= (f(B)B^-1)[B(B-x₀)^-1] ò_[B,C] sin (t-x₀) dt [Wat1, p.66, l.-5].
The absolute value of the last integral is less than or equal to 2w^-¹.
II. Case x₀ < 0.
ò_[B,B'] (f(t)t^-1)[t(t-x₀)^-1] sin (t-x₀) dt
= B'(B'-x₀)^-1 ò_[C,B'] (f(t)t^-1) sin (t-x₀) dt [Wat1, p.66, l.-5]
= B'(B'-x₀)^-1 (f(C)C^-1) ò_[C,D] sin (t-x₀) dt [Wat1, p.66, l.-5].
The absolute value of the last integral is less than or equal to 2w^-¹. Note that f(C)C^-1 £ f(B)B^-1.

Prove [Tit, p.5, (1.3.4)] using the calculus of residues.
Proof. Use the contour [-R+ai, R+ai]+[R+ai, R+bi]+[R+bi, -R+bi]+[-R+bi, -R+ai].
Then let R®+¥. Note that (1+iw)^-1 = i^-1(w-i)^-1.

Prove that ò_[lx,_lh] (sin v)v^-1 dv is bounded for all l and x, where h is fixed and 0<x<h [Tit, p.13, l.-5].
Proof. The integral can be considered an alternating series where the absolute values of its terms are decreasing. Consequently, the absolute value of the integral is less than or equal to
2ò_[0,p] (sin v)v^-1 dv.

Prove the equality given in [Tit, p.16, l.-3].
Proof. lim_l®¥ò_[0,T] [f(x+y) + f(x-y)](sin ly)y^-1dy = 2^-1[f(x+0) + f(x-0)] (by [Tit, p.14, l.2]).
Namely, lim_l®¥ò_{[x-T, x+T]} f(t) [sin l(x-t)](x-t)^-1dt = 2^-1[f(x+0) + f(x-0)].
Since f º 0 on (-¥,0), we have
lim_l®¥ò_{[0, x+T]} f(t) [sin l(x-t)](x-t)^-1dt = 2^-1[f(x+0) + f(x-0)].
Replace T with T-x.

Prove that ò_[T,¥] f(t)(t-x)^-1cos{y(t) - l(x-t)}dt ® 0 as l®+¥ [Tit, p.24, l.3-l.4].
Proof. We may assume that t ³ TÞ 0< f(t)[y'(t]^-1< 1.
Then f(t)[y'(t)+l]^{- 1}= {y'(t)[f(t)]^-1+l[f(t)]^-1}^-1 £ f(t)/l = o(1) as l®+¥.
ò_[T,¥] f(t)(t-x)^-1cos{y(t) - l(x-t)}dt = O{T^-¹ max[f(t)[y'(t)+l]^-1]} [Tit, p.22, Lemma].

Prove |w^(r)(z₀)| £ W^(r)(z₀) [Inc1, p.286, l.6].
Hint. [Bir, p.84, (7); p.94, Lemma].
Remark 1. In [Inc1, p.285, l.-12], Ince let P_n^(r) = M_n /(a^r). [Bir, p.94, (27')] suggests a better choice: let P_n^(r) = |p_n^(r)|. Indeed, Birkhoff's choice can simplify the proof given in [Inc1,§12.22] somewhat.
Remark 2. In order to illustrate Cauchy's method of majorants, one should display concrete formulas rather than use abstract language [Inc1, p.286, l.1-l.6]. Since the general case is so complicated that the key idea is obscured, it is better to discuss only the case n=2.¬

Prove the statement given in [Sak, p.210, l.7-l.9].
Proof.
Let d = min_i_¹1 r(S_i,S₁)>0. Find bi that satisfies r(a_i, b_i) < d.

Prove ò_{(-¥, +¥)} |F(t)| dt < + ¥ [Sak, p.233, l.-2-l.-1].
Proof. If a > 1, ò_{(R,
+¥)} t^-a dt = (-a+1)^-¹R^-a+1.
If a < 1, ò_{(0, a]} t^-a dt = lim _e®₀₊ ò_{[e, a]} t^-a dt = lim _e®0₊ (-a+1)^-1(a^-a+1-e^-a+1).¬

Prove W(z) ³ M + e [Ahl, p.242, l.9].
Proof. M[w(z)w₀^-1-1]+[1-w(z)w₀^-1] f (z₀) = [w(z)w₀^-1-1][M - f (z₀)] ³ 0.

Prove if tÎG, then {2w₁, 2w₂} is a reduced pair of fundamental periods [Gon1, p.370, l.-9-l.-8].
Proof. In order to find a reduced pair of fundamental periods, we must consider periods of the general form:
w = 2mw₁+2nw₂. We try to find a reduced pair among the choices {2w₁, 2w} because (|t|³1 Þ (w₁ is a nonzero period with smallest absolute value)).
Consider the following cases:
(a). n=0: Im (w/w₁) = 0 [Gon1, p.370, l.-7-l.-5].
(b). nÏ{0, 1, -1}: |w| > |w₂| [Gon1, p.371, l.16-l.22].
(c). n = -1 and m = 0: Im (w/w₁) <0 [Gon1, p.371, l.5-l.6].
(d). n = -1 and m ¹ 0: Im (w/w₁) <0 [Gon1, p.371, l.14-l.15].
(e). n = 1 and m = 0: max (|w₁|, |w₂|) < |w| [Gon1, p.371, l.1-l.5].
(f). n = 1 and m ¹ 0: |w| = |w₂| [Gon1, p.371, l.7-l.11].
Since we are looking for a reduced pair among the choices {2w₁, 2w},
we must discard the cases (a), (b), (c), and (d) from our consideration.
By (e) and (f), {2w₁, 2w₂} is a reduced pair of fundamental periods.
Remark. In [Gon1, p.371, l.5], González claims that {2w₁, 2w₂} is a reduced pair. This statement is false because he proves |w| ³ |w₂| only in the case n = ±1 [Gon1, p.371, l.1] but fails to prove |w| ³ |w₂| in other cases when he makes this claim. Similarly, the statement given in [Gon1, p.371, l.11-l.12] is incorrect.

Prove if both endpoints of J lie in {a, b}, then E Í {a, b} [Nar, p.45, l.-2].
Proof. If there were a point pÎE-{a, b}, then J would not be [a, b].
Remark. We may assume E-{a, b}¹Æ in the beginning of the proof of [Nar, p.45, Lemma 4]. This is because if E-{a, b}=Æ, then the proof of [Nar, p.45, Lemma 4] is trivial.

Prove the formula given in [Wat1, p.256, l.13], where m and n have their real parts positive.
Proof. G(z)^-1 = ze^gzÕ_n=1^¥(1+zn^-1)e^-z/n.
By Stirling's formula, G(z)®¥ as z®¥.
Consequently, G(z)^-1 is analytic at z = ¥, a limit point of the set of positive integers.

Prove f '(z) = (2pi)^-1ò_g f '(t)f'(z)[f(t) - f(z)]^-1dt [Wat1, p.129, l.-4].
Proof. Fix z. g can be replaced by a small circle centered at z.
f(t) - f(z) = (f'(t) + e)(t - z).

Prove the statement given in [Wat1, p.304, Example 1].
Proof. Differentiate Riemann's P-equation satisfied by d^r P_n(z)/d z^r with respect to z.

Prove that ò_{[a, b]} f(y)K(x, y) dy given in [Wat1, p.212, l.7] is a continuous function of x Î [a, b].
Proof. z¯x+ Þ ò_{[a, z]} f(y)K(z, y) dy ® ò_{[a, x]} f(y)K(x, y) dy [Ru2, p.27, Theorem 1.34].

Prove the statement given in [Wat1, p.81, Example 11].
Proof. We must assume that f (x,y) is bounded on [a,b]².
It suffices to prove that y_n®y Þ ò_[a,b]f(x,y_n)dx® ò_[a,b]f(x,y)dx   ().
Let D₀ = {xÎ[a,b]| f is discontinuous at (x,y)} and
D_n = {xÎ[a,b]| f is discontinuous at (x,y_n)}, where n = 1,2,….
Then D = È_{kÎ{0,1,2,…}}D_k is countable.
f(x,y_n)®f(x,y) on [a,b]-D as y_n®y.
() follows from [Ru2, p.27, Theorem 1.34].
Remark. The hint given in [Wat1, p.81, l.-3-l.-1] is useless. There are three levels of understanding a subject. The first level is to read a textbook and study it word by word from beginning to end. The second level is to read several books on the same field and understand their merits and drawbacks. The third level is to write a book on the subject and provide the most accessible approach to master the subject. One should not omit or touch on lightly the difficult part. On the contrary, one should analyze it more elaborately and strive to find the key to understanding its crucial point.
    There are several factors that may increase a reader's difficulty in understanding mathematics books:

Unclear explanation as the above example.

Misguidance due to lack of preparation: Compare [Wat1, p.217, l.20-l.21] with [Boc, p.41, l.-12].

A gap in the argument: The statement given in [Wat1, p.217, Example 1] should have been inserted between [Wat1, p.216, l.-10] and [Wat1, p.216, l.-9]. See [Boc, p.35, l.13-15].

The assumption is not clearly specified beforehand. [Wat1, p.321, l.14-p.322, l.8] discusses t, but fails to specify its domain. Later, [Wat1, p.322, l.9-l.10] specifies that t is on an ellipse. Consequently, until then readers have no way to understand the exact meaning of uniform convergence given in [Wat1, p.322, l.8].
    It is inappropriate for one who understands a subject at the basic level to do the advanced-level work. This is a reason that modern textbooks and journals lack educational value.¬¬

Prove the equality given in [Wat1, p.214, l.7].
Proof. The term containing the factor (- l d )³ is the sum of the determinants of the form

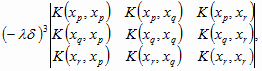
where p < q < r.

Prove the equality about the series expansion of D_n(x_m,x_n) in [Wat1, p.214].
Proof. Let n = 5.
Step 1. By crossing out the fourth column and the fifth row of D₅(l), we obtain D₅(x₄,x₅), a 4´4 matrix.
Step 2. Consider the term containing the factor (-ld)² in D₅(x₄,x₅). In order to form a product term for the determinant
D₅(x₄,x₅) that contains the factor (-ld)², we must choose two terms on the diagonal that contain the constant 1, say elements (1,1) and (2,2). They cannot be (4,4) because 1-ldK(x₄,x₄) was crossed out during Step 1. Consequently, the term -ldK(x₄,x₅) remains as a chosen factor for the product that we desire to form. In fact, by crossing out the first and second rows and the first and second columns, we obtain

Prove that [Hob, p.186, (b)] is valid when Re a > 0, Re b > 0, and Re r > 0.
Proof. [Wat1, p.257, l.-7].

Derive [Hob, p.189, (12)] from [Hob, p.188, (11)].
Proof. Use [Guo, p.204, Exercise 6].

Prove the formula given in [Hob, p.190, l.-2].
Proof. This is [Wat1, p.299, Exercise 6]. We can use [Wat1, p.291, l.3-l.5] to prove the formula given in [Wat1, p.299, l.2]. The term on [Wat1, p.291, l.4] can be ignored when compared with term on [Wat1, p.291, l.5].
lim _x®1- F(a,b;g; x)[- log (1-x)]^-1
= lim _x®1- [abg^-1 F(a+1,b+1;g+1; x)][(x-1)^-1]^-1 [Wat1, p.281, l.-14; l'hôpital's rule]
= abg^-1G(g+1)[G(a+1)G(b+1)]^-1 [Wat1, p.299, l.2].

Let z = a + be^if. When f increases 2p, arg z increases 2p if |b|>|a|; arg z does not change if |b|<|a| [Wat1, p.329, l.1-l.3].
Proof. If |b|<|a|, let b®0. If |b|>|a|, let a ® 0; the image of z circles the origin once counterclockwise.

Prove ò_Cl^k(lI-T)^-1 dl=T^k [Dow, p.12, l.-3].
Proof. The proof given in [Dow, p.12, l.-4-l.-3] is incorrect. By [Dow, p.3, Theorem1.4] and Cauchy's integral theorem [Dun, vol.1, p.226, l.-13], we may replace C in [Dow, p.12, l.-5] with C'={l:|l|=||T||+e}. Once we replace C in [Dow, p.12, l.-4] with C', we correct Dowson's mistake.

Solve [Cod, p.97, Problem 1].
Proof. Existence: Use an argument similar to that solving [Cod, p.38, Problem 4].
Uniqueness: Let h₁ and h₂ be two solutions.
In [Cod, p.37, Problem 1], let j = |h₁-h₂|, y(t) = 0, and c(t) = k(t).

[Cod, p.106, Problem 40]
Proof. By [Jaco, vol.2, p.86, Theorem 6], we have a cyclic decomposition given in [Jaco, vol.2, p.92, l.-7-l.-5].
By [Jaco, vol.2, p.70, Theorem 3], we have a more refined secondary decomposition given in we have a [Jaco, vol.2, p.93, l.-1-p.94, l.1].
Thus, we may assume R={f} and the minimum polynomial of f is (l-c)^e, where c=a+bi.
Let {f} = [P₁,P₂,…,P_e], where P_j=X_j+iY_j.
Then AP_j= cP_j+P_j+1 (j = 1,…,e-1) and
AP_e= cP_e.
The matrix of A relative to the basis {X_e,Y_e,…,X₁,Y₁} has the desired form.

[Cod, p.107, Problem 41]
Proof. Let . Then J² = -E₂.
exp(tJ)= E₂+(tJ)/(1!)+(tJ)²/(2!)+…
= [1-t²/(2!)+t⁴/(4!)+…]E₂+[t/(1!)-t³/(3!)+…]J
= .
exp(log(a_j²+b_j²)^1/2E₂+[tan^-1(b_j/a_j)]J) = exp(log(a_j²+b_j²)^1/2E₂) exp([tan^-1(b_j/a_j)]J) [Dow, p.15, Theorem 1.23(ii)].

Prove the formula given in [Wat1, p.109, Example 6].
Proof. We want to prove S_k=0ⁿ[(m)_k/k!]z^k(1-z)^m+ [(m)_n+1/n!]ò_[0,z]tⁿ(1-t)^m-1 dt = 1.
By differentiation, it suffices to prove S_k=0ⁿ[(m)_k/k!][kz^k-1(1-z)^m - mz^k(1-z)^m-1] + [(m)_n+1/n!] zⁿ(1-z)^m-1 = 0.
S_k=0ⁿ[(m)_k/k!][kz^k-1(1-z) - mz^k] = -m + S_k=0ⁿ[(m)_k/k!][kz^k-1 - (k+m)z^k] = -[(m)_n+1/n!] zⁿ.

Prove the equalities given in [Wat1, p.349, l.-3].
Proof. By [Wat1, p.347, l.16-l.19], D_n(0) = G(1/2)2^n/2/G((1-n)/2) and D'_n(0) = G(-1/2)2^(n-1)/2/G(-n/2).
Differentiate the equality given in [Wat1, p.349, l.-15]. Then solve a and b.

Prove the statement given in [Wat1, p.358, Example 1].
Proof. exp[z(t-t^-1)/2] = S tⁿ J_n(z)                   ()
Differentiating () with respect to z once, we have J_n' = (J_n-1-J_n+1)/2.
Differentiating () with respect to z twice, we have J_n" = (J_n-2-2J_n+J_n+2)/4.
Differentiating () with respect to t, we have J_n+J_n+2 = [2(n+1)/z] J_n+1.¬

Prove the statements given in [Wat1, p.358, Example 2].
Proof. The first statement follows from [Guo, p.71, (16); p.70, (10)]. The second statement follows from [Guo, p.69, (3)].

Prove the equality given in [Wat1, p.366, l.4].
Proof. See [Guo, p.354, Fig. 25].
Let arg (1 - t²) = 0 if -1< t <1.
On the path from -1 to 1, (t - 1)^n-1/2 = exp{(n - 1/2)[log (1 - t) - ip]}.
On the path from 1 to -1, (t - 1)^n-1/2 = exp{(n - 1/2)[log (1 - t) + ip]}.

Prove the equality given in [Wat1, p.367, l.-5].
Proof. Replace z in the expression given in [Wat1, p.367, l.17] by cos (z/n).
Let the (r+1)th term of the series given in [Wat1, p.369, l.-9] be f_r and
f_n,r be the expression obtained by replacing (z/n)^2r with(n sin [z/(2n)])^2r.
Then f_n,r®f_r as n®¥ because lim_n®¥ (sin [z/(2n)])[z/(2n)]^-1 = 1.

Prove the statements given in [Wat1, p.371, Example 1 & Example 2].
Proof. Read [Wat, p.58, l.3-p.59, l.9].

Prove [Guo, p.359, (19)].
Proof. Let G = {c+Re^iq|(p/2)+R^-d £ q £ p}.
It suffices to prove ò_G e^tt^-n-1dt ®0 as R®+¥.
Take d>0 such that (Re n)+1 > (d+d²)/2.
cos ((p/2)+R^-d) = - sin (R^-d) £ -2p^-1R^-d.
|ò_G e^tt^-n-1dt| £ e^ce^{- (2/p) R^-d+1} R^{-Re n}.
e^-x £ x^{- [1+(d/2)]} when x is sufficiently large.

Prove [Guo, p.430, Problem 20].
Proof. Use [Wat1, p.360, (C); p.359, (A); p.359, l.4].¬

Prove [Guo, p.426, Problem 5].
Proof. I. Read [Wat, p.27, l.-11-l.-8]: Express _2nC_2m+1 and _n-1C_m in terms of the gammer function in order to find their quotient; cos nq + i sin nq = (cos q + i sin q)ⁿ.
II. In order to derive [Guo, p.364, (20)] from [Guo, p.364, (19)], we use [Wat, p.26, l.-6-p.27, l.4; p.22, (1), (2), (3), (4)].

Prove the statements given in [Wat, p.163, l.15-l.17].
Proof. ò_¥i^{(-+,
1+)} t^2n-1-2m e^izt dt = ò_¥i⁽⁰⁺⁾ t^2n-1-2m e^izt dt.
Let u = -izt.
t^2n-1-2m dt = (-1)^-nmz^2m-2n u^2n-1-2m du.
-[G(z)]^-1 = (2pi)^-1 ò _¥⁽⁰⁺⁾ e^-t(-t) ^-z dt (|arg (-t)|<p) [Wat1, p.345, l.-8]
= (2pi)^-1 ò _{¥ exp ia}⁽⁰⁺⁾ e^-t(-t) ^-z dt.

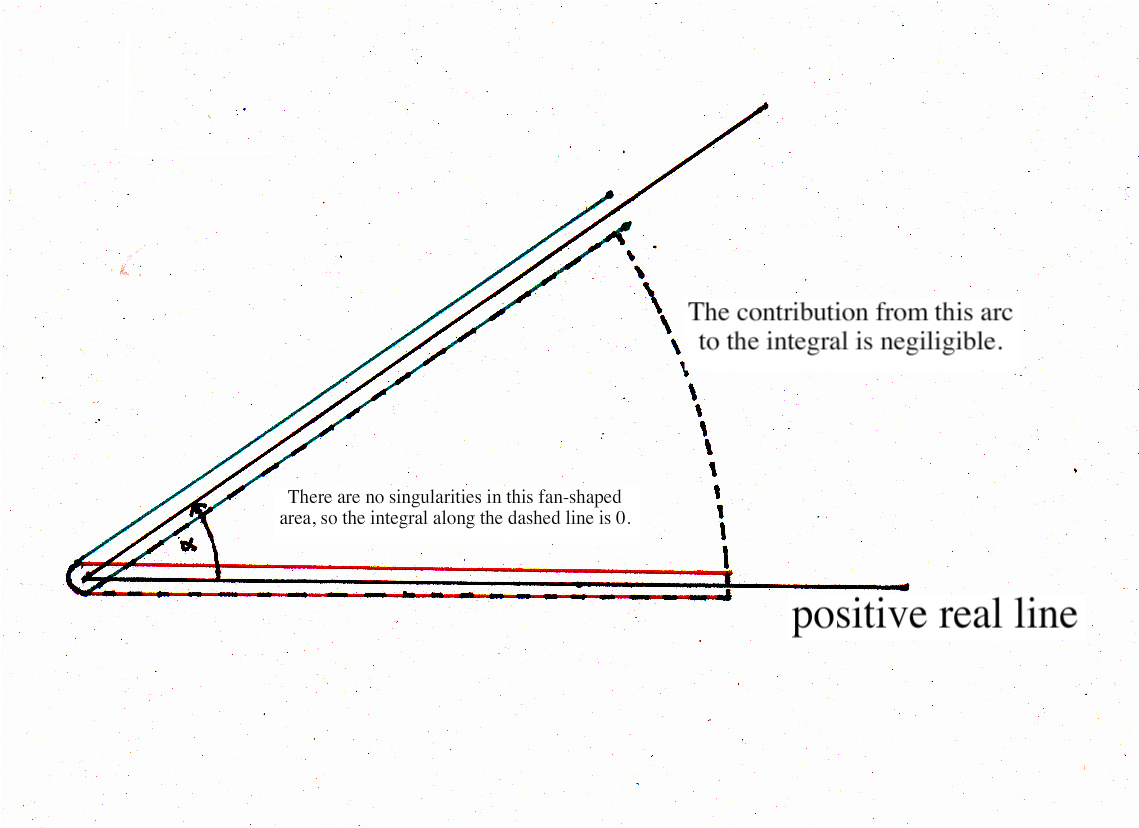
The contribution from the above arc is negligible because |a|<p/2.

Prove the equality given in [Guo, p.371, l.8].
Proof. The -w given in [Wat, p.167, (6)] refers to the angle rotated about the branch point t = 1. Let w = p/2. The restriction given in [Wat, p.164, l.6] is unnecessary, see [Wat, p.167, l.4]. After the rotation, on the first half of the contour, arg (t - 1) = -2p; on the second half of the contour, arg (t - 1) = 0.
[e^-2pi - e⁰ⁱ](t - 1) = [e^-2pi - e⁰ⁱ] e^pi (1 - t) = [e^-pi - e^pi] (1 - t).

If (¶/¶t + ¶/¶z) F(z, t) = 0, then F(z, t) is expressible as a function of t - z [Wat1, p.376, l.18].
Proof. Use the following invertible linear transformation: Let u = t + z, v = t - z, and F(z, t) = G(u, v).
¶G/¶u = 0 Þ G is independent of u.

Prove the statements given in [Wat1, p.392, l.-6-l.-1].
Proof. Zonal harmonics: n parallels of latitude [Col, p.233, l.5].
Tesseral harmonics [cos mf P_n^m (cos q)]: n - m parallels of latitude [Wat1, p.323, l.-5] and 2m meridians.

Prove sin u sin (v - f) = sin w sin y [Wat1, p.397, l.-3].
Proof.
Without loss of generality, we may assume f = 0.
Let A = (sin u cos v, sin u sin v, cos u).

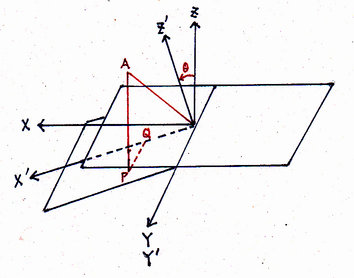
We first find the equation ax + by + cz = 0 of the X'Y'-plane.
Since (0,1,0) and (cos q, 0, - sin q) are on this plane, we have b = 0 and a/c = (sin q)/(cos q).

Let L be the line that passes through A and is perpendicular to the X'Y'-plane.
L: (x, y, z) = (sin u cos v, sin u sin v, cos u) + t (sin q, 0, cos q).

Find the intersection P of L and the X'Y'-plane.
sin q (sin u cos v + t sin q) + cos q (cos u + t cos q) = 0.
t = - (sin q sin u cos v + cos q cos u).
P(x,y, z)=(sin u cos v - sin² q sin u cos v - sin q cos q cos u,sin u sin v,cos u - sin q cos q sin u cos v - cos² q cos u).
Let PQ be the line that passes through P and is parallel to the Y'-axis, where PQ and the X'-axis intersect at Q.
Then P + s (0,1,0) = Q.
P_y+ s = Q_y= 0.
s = - sin u sin v.
PQ = |P-Q| = sin u sin v.
sin y = PQ/OP = (sin u sin v)/ sin w.

Remark. The formula looks simple, but there is no simple geometric method to prove it. Its proof still requires nontrivial calculations. One learns lessons from every failed attempt. The more we try, the clearer the access becomes. If one proves this formula oneself, one will learn a lot about rotations and projections.

(Worpitzky's theorem) Let a₂, a₃, a₄, … be functions of any variables over D in which |a_p+1|£1/4, p = 1,2, 3, …. Prove that
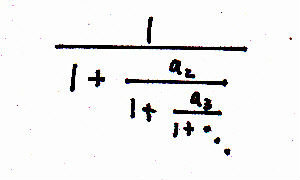
$continued-fraction-worpitzky$
converges uniformly over D; 2 is the upper bound for the absolute value of the above continued fraction.
Proof. [Wal, p.42, Theorem 10.1(a); A Convergence Theorem for Continued Fractions, by W. T. Scott and H. S. Wall (1939), p.159, l.-14-l.-11].

Prove the the equality given in [Inc1, p.182, l.6].
Proof. [Perr, p.292, Satz 46D].

Prove the statements given in [Har, p.46, Exercise 1.2].
Proof. We may assume that A(t) is a 1x1 matrix.
F: C([t₀-r, t₀+r], [y₀-R, y₀+R])®C([t₀-r, t₀+r], [y₀-R, y₀+R])
F(y) = y₀ + ò_{[t₀, t]} A(s)y(s) ds.
||F(y) - y₀|| £ |ò_{[t₀, t]} |A(s)| ds| ||y||.
||F(y) - F(z)|| £ |ò_{[t₀, t]} |A(s)| ds| ||y-z||.
ò_{[t₀, t]} |A(s)| ds®0 as r®0.
The existence and uniqueness follows from the Banach fixed point theorem.
The method given in the proof of [Cod, p.20 Theorem 5.1] can be used for domain expansion.

The inverse of an invertible upper triangular matrix A is upper triangular [Har, p.49, Exercise 2.1].
Proof. Let B_ij be the matrix that results when the ith row and jth column of A are deleted.
It suffices to that det (B_ij) = 0 if i < j.
B_ij is upper triangular, so the (i+1)st row of A begins with at least i zeros.
Since i < j, none of the first i zeros is removed by deleting the jth column.
The ith diagonal element of B_ij is 0, so det (B_ij) = 0.

Prove the inequality given in [Cod, p.37, l.-8].
Proof. j(s) - ò_a^s c(s) j(s) ds £ y(s)
Þ c(s)j(s) - c(s) ò_a^s c(s) j(s) ds £ c(s)y(s)
Þ R'(s)- c(s) R(s)£ c(s)y(s).
R'(s)exp( ò_s^t c(u) du) - c(s) R(s) exp( ò_a^s c(u) du) £ c(s)y(s)exp( ò_s^t c(u) du)    ().
The left side is (d/ds) [R(s) exp( ò_a^s c(u) du)].
Integrate both sides of ().

Prove the formula given in [Inc1, p.120, l.-2].
Proof. The two sides of the equality are linear differential operators of order r whose coefficient of u^(r) is D_r². Since u₁, …, u_r are solutions of the corresponding homogeneous ODEs of both operators, by [Cod, p.70, l.-9], the two differential operators are equal.

Prove the formula given in [Cod, p.141, l.3].
Proof. I. |j(t)-e^it+aò_t^{^¥} sin (t-t)e^it(S_k=0ⁿ c_kt^-k)t^-2dt|
= |aò_t^{^¥} sin (t-t)e^it(-j(t)+S_k=0ⁿ c_kt^-k)t^-2dt|
£|a|ò_t^{^¥} At^-(n+1)t^-2dt                  (by the induction hypothesis)
= O(t^-(n+2)).
II. aò_t^{^¥}[e^it-e^-it+2ti](2i)^-1(S_k=0ⁿ c_kt^-k)t^-2dt
= ae^it(2i)^-1(S_k=0ⁿ c_kt^-(k+1)(k+1)^-1)+ae^it(2i)^-2(S_k=0ⁿ c_kt^-(k+2))
+ae^it(2i)^-3(S_k=0ⁿ c_k(k+2)t^-(k+3))+…
+ae^it(2i)^-(n+1)(S_k=0ⁿ c_k(k+2)…(k+n)t^-(k+n+1))+ae^it(2i)^-(n+1)(S_k=0ⁿ c_k(k+2)…(k+n)(k+n+1)ò_t^{^¥} e^2tit^-(k+n+2)dt).
Using integration by parts, we have ò_t^{^¥} e^2tit^-(k+n+2)dt = O(t^-(n+2)).
III. By II, aò_t^{^¥} sin (t-t)e^it(S_k=0ⁿ c_kt^-k)t^-2dt
= ae^it[(S_k=0ⁿ (2i)^-1c_k(k+1)^-1t^-(k+1))+(S_k=1ⁿ⁺¹ (2i)^-2c_k-1t^-(k+1))+(S_k=2ⁿ⁺² (2i)^-3c_k-2kt^-(k+1))
+…+(S_k=n^n+k (2i)^-(n+1)c₀ k!t^-(k+1))+O(t^-(n+2))]
= ae^it(S_k=0ⁿ [(2i)^-1c_k(k+1)^-1+(2i)^-2c_k-1+(2i)^-3c_k-2k +…+(2i)^-(k+1)c₀ k!]t^-(k+1)+O(t^-(n+2)).
Note that (m>n)Þ[c_k-m = 0      (k=0, 1,…, n)].
IV. By induction and [Cod, p.139, (1.5)] , we can prove
- c_k+1= a[(2i)^-1c_k(k+1)^-1+(2i)^-2c_k-1+(2i)^-3c_k-2k +…+(2i)^-(k+1)c₀ k!].
Remark. The O constant depends on n.

(The asymptotic expansion of the Whittaker function)
Prove [Guo, p.307, (2)] using Watson's lemma.
Proof. I. ò_¥⁽⁰⁺⁾ e^-t(-t)^-k-1/2+m(1+t/z)^k-1/2+m dt
= z^-k+1/2+m ò_¥Exp(ia)⁽⁰⁺⁾ e^-t(-t)^-k-1/2+m(1+t/z)^k-1/2+m dt, where a = arg z.
II. Let f(t) = (-t)^-k-1/2+m(1+t)^k-1/2+m.
|f(t) - (-t)^-k-1/2+m S_n=0^N-1 C(k-1/2+m, n)tⁿ|£ Mt^{Re(-k+m)+1/2+N}e^{-(arg t)Im(-+m)} in some neighborhood of t=0.
|f(t) - (-t)^-k-1/2+m S_n=0^N-1 C(k-1/2+m, n)tⁿ|£ Ke^e|t||t|^N for t¹0.
|ò_¥Exp(ia)⁽⁰⁺⁾ e^-zt f(t)dt - S_n=0^N-1 C(k-1/2+m, n)ò_¥Exp(ia)⁽⁰⁺⁾ e^-zt (-t)^-k-1/2+m tⁿdt|
£ K ò_¥⁽⁰⁺⁾ e^{-(Re z -e)|t|}|t|^N|dt|
= K ò_¥⁽⁰⁺⁾ e^-|t||t|^N(Re z -e)^-(N+1)|dt|
= O((Re z -e)^-(N+1))=[|z|/(Re z -e)]^-(N+1)O(|z|^-(N+1)).
III. |arg z|£(p/2) - d
Þ Re z ³|z| sin d
Þ Re z|/(Re z -e) £ 2/(sin d).
IV. ò_¥Exp(ia)⁽⁰⁺⁾ e^-zt (-t)^-k-1/2+m tⁿdt
= (-1)ⁿò_¥Exp(ia)⁽⁰⁺⁾ e^-zt (-t)^-k-1/2+m+n dt
= (-1)ⁿz^k-1/2-m-nò_¥⁽⁰⁺⁾ e^-t (-t)^-k-1/2+m+n dt
= (-1)ⁿz^k-1/2-m-n(-2pi)G(k+1/2-m-n)^-1, since |arg (-t)|<p(by [Guo, p.102,(4)).
V. By II, III, and IV, W_k,m ~ e^-z/2z^kS_n=0^¥ (-1)ⁿG(k+1/2-m)G(k+1/2+m)G(k+1/2-m-n)^-1G(k+1/2+m-n)^-1.
By [Guo, p.99, (2)], we have the desired result.

Prove the statement given in [Inc1, p.214, l.-12].
Proof. "The rank of both matrices is n-k" means that the row of coefficients in (D) can be expressed as a linear combination of the rows of coefficients in (E). Namely,
U₁(c₁u₁+…+c_nu_n) = U₁(u₀) - g₁
U₂(c₁u₁+…+c_nu_n) = U₂(u₀) - g₂
…
U_n(c₁u₁+…+c_nu_n) = U_n(u₀) - g_n.
Let u = u₀ - (c₁u₁+…+c_nu_n), then u is a solution of (A).

Replace F = sup |j| given in [Cod, p.46, l.5] with F = sup j and then prove the continuity of F.
Proof. "e>0, ($d>0)(|t-t'|<dÞ|M(t)-M(t')|<e).
($j₁)(|F(t)-j₁(t)|<e).
($j₂)(|F(t')-j₂(t')|<e).
Let j_M = max (j₁,j₂).
|F(t)-F(t')|£|F(t)-j_M(t)|+|j_M(t)-j_M(t')|+|j_M(t')-F(t')|.
The desired result follows from [Cod, p.45, (1.11)].

Prove the equality given in [Inc1, p.195, l.14].
Proof. [x(d/dx)]F(z)=xt(dF/dz)=[t(d/dt)]F(z).
G(x(d/dx))K = G(t(d/dt))K.
(xt)ⁿF(x(d/dx)) = zⁿF(z(d/dz))K = H(z(d/dz))K = H(t(d/dt))K.

Replace the term -Kaw by -2^-1Kaw given in [Inc1, p.198, l.2] and then prove the equality.
Proof. d(Kaw)=(aw)[(¶K/¶s)ds+¶K/¶t)dt]+[¶(aw)/¶s)ds]Kds+[¶(aw)/¶t)dt]Kdt.
ò[¶(aw)/¶s)]Kds = òò[¶(aw)/¶s)](¶K/¶t)dsdt+òòK[¶²(aw)/(¶s¶t)]dtds
= òaw[¶K/¶t]dt-òòaw[¶²K/(¶s¶t)]dsdt+òòK[¶²(aw)/(¶s¶t)]dtds.
Exchanging s and t in the last equality, we have
ò[¶(aw)/¶t)]Kdt = òaw[¶K/¶s]ds-òòaw[¶²K/(¶t¶s)]dtds+òòK[¶²(aw)/(¶t¶s)]dsdt.

[Cod, p.201, Problem 1].
Proof. Þ:
L₂=-px"-p'x'+qx.
L₂⁺= - px'' - p'x'+ qx.
L₂=L₂⁺Þ(p and q are real).
We may take real solutions u, v and let a,b,g,d be real.
Ü:
(Lu,v)-(u,Lv) = p(t)(u(t) v'(t)-u'(t) v(t))|_a^b [Cod, p.224, (1.9)].
If a,b are real, then [(u and v satisfy the first boundary condition)Þu(a) v'(a)-u'(a) v(a)=0].
If g,d are real, then [(u and v satisfy the second boundary condition)Þu(b) v'(b)-u'(b) v(b)=0].
Remark. By this problem and [Bir, p.256, Definition], [Bir, chap.10] may omit discussing the concept of self-adjointness on the one hand. Thus, it misses this important topic on the other hand.

[Cod, p.201, Problem 2].
Proof. I. Let U₁ = u(b)- au(a)-bu'(a) = 0,
U₂ = u'(b)- gu(a)-du'(a) = 0,
U₃ = u(a) and
U₄ = u'(a).
U₁V₄+U₂V₃+U₃V₂+U₄V₁
= ò_a^b( v Lu-u Lv) dt [Inc1, p.211, l.-11-l.-10]
= p(t)(u(t) v'(t)-u'(t) v(t))|_a^b [Cod, p.224, (1.9)].
By comparing the coefficients of the first term with those of the last term, we have
V₂-aV₄-gV₃ = -p(a) v '(a).
V₁-bV₄-dV₃ = p(a) v (a).
V₄ = p(b) v '(b).
V₃ = -p(b) v (b). Consequently,
V₂ = -p(a) v '(a)+ap(b) v '(b)-gp(b) v (b);
V₁ = p(a) v (a)+bp(b) v '(b)-dp(b) v (b)   (*).
II. In order that the given system may be self-adjoint, it is necessary and sufficient that V ₁(v) and -d₂(v) should each be a linear combination of U₁(v) and U₂(v).
Since v'(a) does not enter into V ₁, V ₁ may be obtained by eliminating v'(a) between U₁(v) and U₂(v).
V ₁=c(d₁₃ v (a)+d₂₃ v (b)+d₄₃ v '(b)) = p(a) v (a)+p(a) (d₁₃)^-1(d₂₃ v (b)+d₄₃ v '(b)) (**) [Inc1, p.216, l.2].
By comparing (*) with (**), we have b(b)^-1 = d(d)^-1 = p(b)(p(a))^-1d₁₃.
Similarly, a(a)^-1 = g(g)^-1 = p(b)(p(a))^-1d₁₃.

[Cod, p.201, Problem 3].
Solution. p_n-jÎC^n-j given in [Cod, p.201, l.-4] should have been corrected as p_n-jÎC^2j.
I. It suffices to prove (L_2n = L_2n⁺) Þ (L_2(n+1) = L_2(n+1)⁺).
Proof. L_2(n+1) = L_2n +(p₀x⁽ⁿ⁺¹⁾)⁽ⁿ⁺¹⁾ = L_2n + S_j=0ⁿ⁺¹C(n+1,j) p₀^(j)x^(2n+2-j).
L_2(n+1)⁺ = L_2n⁺ + S_j=0ⁿ⁺¹(-1)^j C(n+1,j) (p₀^(j)x)^(2n+2-j)
= L_2n + S_j=0ⁿ⁺¹(-1)^j C(n+1,j) S_k=0^2n+2-jC(2n+2-j,k) p₀^(j+k)x^(2n+2-j-k)
= L_2n + S_m=0²ⁿ⁺²S_j=0ⁿ⁺¹(-1)^j C(n+1,j) C(2n+2-j,m-j) p₀^(m)x^(2n+2-m).
Thus, it suffices to prove C(n+1,m) = S_j=0ⁿ⁺¹(-1)^j C(n+1,j) C(2n+2-j,m-j) for integers m Î[0,n+1].
II. S_j=0ⁿ⁺¹(-1)^j C(n+1,j) C(2n+2-j,m-j) = (-1)^m S_j=0ⁿ⁺¹ C(n+1,j) C(m-2n-3,m-j) (by upper negation)
=(-1)^m C(m-n-2,m) (by Vandermonde's identity)
=C(n+1,m) (by upper negation).
III. (Lu,v) - (u,Lv)=[uv]|_a^b (by L_2n = L_2n⁺ and [Cod, p.86, (6.11)])
=0 (by [Cod, p.86, (6.12)] and the boundary conditions).

Prove [Mari, p.505, (12.160)].
Proof. Let D_n(x)=S_k=-nⁿ e^ikx. Then D_n(0)=2n+1.
By [Ru1, p.174, (77)], D_n(rp/(n+1))=(-1)^r+1 if r¹0.
S_j=1ⁿ sin (jrp/(n+1))sin (jsp/(n+1))
=-4^-1[D_n((r+s)p/(n+1))-D_n((r-s)p/(n+1))].
Remark. Let {U_n} be a complete orthonormal set in L²[a, b]. Then
"fÎL²[a, b], f(x)=S_n=1^¥ a_nU_n(x), where a_n= ò_a^b U_n^(x')f(x')dx'. Then
f(x)= ò_a^bS_n=1^¥U_n^(x')U_n(x)f(x')dx' (fÎL²[a, b]).
By [Ru2, p.31, Theorem 1.39(b)], S_n=1^¥U_n^*(x')U_n(x)= d(x-x').

Let D=d/(d cos q). If D^n-1 sin ^2n-1q=A sin nq, where A is a constant, prove nA=(-1)^n-11^.3^.5^...(2n-1) [Wat, p.28, l.14].
Proof. D=(-sin q)^-1(d/d q)=(-q)^-1(d/d q)(1-(3!)^-1q²+(5!)^-1q⁴-^...)^-1.
expand the two sides of D^n-1 sin ^2n-1q=A sin nq in ascending series of q and then take the terms of the lowest degree in q.
The term for the right side is Anq.
The term for the left side is [d/(-qdq)]^n-1q^2n-1=(-1)^n-1(2n-1)(2n-3)^...3^.1^.q.

Prove the equality given in [Wat, p.28, l.19; Wat1, p.133, l.11].
Proof. (d²/dm²)[f'(m)f(m)³]=f'''(m)f(m)³+f''(m)[6f²(m)f '(m)]+f'(m)[6f(m)(f '(m))²+3f(m)²f ''(m)].
Then find the corresponding terms h³f⁽ⁱ⁾ in the Taylor expansion
f(z)=f(m)+f'(m)(hf(z))+f''(m)[(2!)^-1(hf(z))²]+f'''(m)[(3!)^-1(hf(z))³]+…, where
f(z)=f(m)+f '(m)(h(f(z))+f ''(m)[(2!)^-1(hf(z))²]+….