then the magnitude of a, written a (or sometimes |a|), is given by:
a2 = x2 + y2 + z2
Proof:
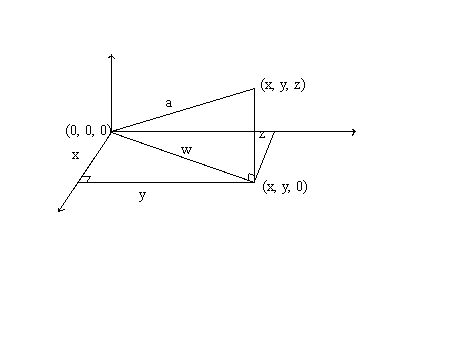
By Pythagoras' theorem
w2 = x2 + y2 and
a2 = w2 + z2
=> a2 = x2 + y2 + z2
All 3D vectors can be represented by a directed line segment in 3D space R3, which has a start point and an end point. This gives each vector a magnitude (the length of the line segment) and direction (from the start point to the end point). They have a rigorous definition in terms of vector spaces, but this'll do for now.
If we take the origin as out starting point we can describe any vector, a, by specifying its end point in cartesian coordinates (x, y, z). So any vector can be described by an ordered 3-tuple (x, y, z) where x, y and z are real numbers. In n dimensional space we could describe any vector by an ordered n-tuple (x1, x2, ... , xn) but we'll stay in 3D.
Definition: The position vector of a point A is the vector represented by the line segment from the origin to A, and is written a.
Given the points A, B, C, let the u be the vector from A to B, and v be the vector from B to C. The vector u + v is the vector from point A to point C. On paper, if
u = (a, b, c) and
v = (x, y, z) then
u + v = (a + x, b + y, c + z)
Multiplying a vector by a scalar leaves the direction of line segment unchanged, but multiplies the length by the scalar. Again, if l
is a real number and
u = (a, b, c) then
l u = (la, lb, lc)
i is the vector from (0,0,0) to (1,0,0)
j is the vector from (0,0,0) to (0,1,0)
k is the vector from (0,0,0) to (0,0,1)
These vectors are the Cartesian vectors which form a basis of R3. This means that any 3D vector a from (0,0,0) to (x, y, z) can be written as a linear combination of i, j, and k like so:
a = xi + yj + zk
To get used to visualizing 3D vectors try testing out this applet
Let a = xi + yj + zk
then the magnitude of a, written a (or sometimes |a|), is given by:
a2 = x2 + y2 + z2
Proof:
By Pythagoras' theorem
w2 = x2 + y2 and
a2 = w2 + z2
=> a2 = x2 + y2 + z2
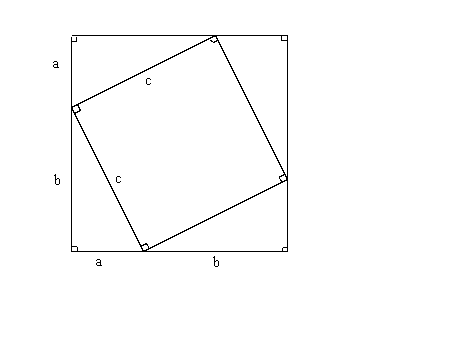
Let x be the area of the larger square, then
x = (a + b)2 but also
x = c2 + 4 (1/2 ab )
=> (a + b)2 = c2 + 2ab
=> a2 + b2 + 2ab = c2 + 2ab
=> a2 + b2 = c2