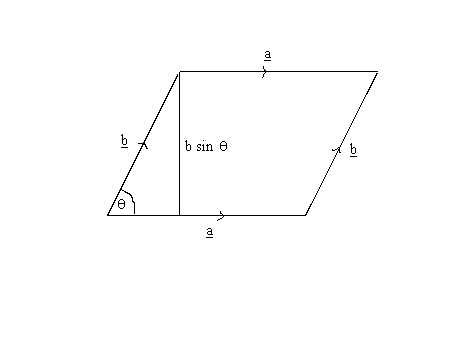The Cross Product

• Definition
• Finding the normal vectors
• Properties of the cross product

The cross product of a and b, written a x b, is defined by:
a x b = n a b sin q
where a and b are the magnitude of vectors a and b; q is the angle between the vectors, and n is the unit vector (vector with magnitude = 1) that is perpendicular (at 90 degrees to/ orthogonal to/ normal to) both a and b. But there are two vectors that this could be - one on either side of the plane formed by the two vectors), so we choose n to be the one which makes (a, b, n) a right handed triad.

Like in the definition of the dot product where we pulled q out of a hat and said it was the angle between the two vectors without any way of finding it, so we need a way of finding n for out definition of the cross product to be any use. Again the i, j, k vectors come to our rescue, giving us an equivalent definition: let,
a = a₁ i + a₂ j + a₃ k
b = b₁ i + b₂ j + b₃ k
then,
a x b = ( a₁ i + a₂ j + a₃ k) x (b₁ i + b₂ j + b₃ k)
The cross product of any two parallel vectors is the null vector since sin 0 = 0, and also
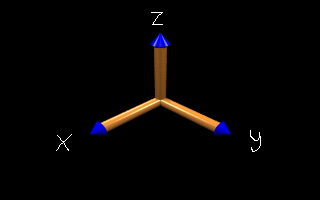
i x j = k
j x k = i
k x i = j
and
j x i = -k
k x j = -i
i x k = -j
Using these, we can eventually find:
a x b = (a₂b₃ - a₃b₂)i + (a₃b₁ - a₁b₃)j + (a₁b₂ - a₂b₁)k
That's our equivalent definition. If you're familiar with determinants you may see this can be written more conveniently as,

    | i    j    k|        
    | a1  a2   a3|  
    | b1  b2   b3| 

Using the equivalence of our two definitions,
a x b = (a₂b₃ - a₃b₂)i + (a₃b₁ - a₁b₃)j + (a₁b₂ - a₂b₁)k = n a b sin q
you can now find n
To get used to the cross product try out this cross product applet

Some Properties of the Cross Product