The Vector Equation of a Plane

Here, we use our knowledge of the dot product to find the equation of a plane in R³ (3D space). Firstly, a normal vector to the plane is any vector that starts at a point in the plane and has a direction that is orthogonal (perpendicular) to the surface of the plane. For example, k = (0,0,1) is a normal vector to the xy plane (the plane containing the x and y axes).
Any three distinct points define our plane, or alternatively, a single point in the plane and a given normal vector to the plane. We'll define it like this first.
All we need is a way of checking whether a given point, with position vector r lies in the plane or not.
Let a be the position vector of the given point in the plane, and
let n be the given normal vector to the plane.
Then r is in the plane if and only if (iff)
(r - a) . n = 0
Explanation: r - a is the vector from A to R, and any vector that lies completely in the plane (like this one does) must be orthogonal to n which implies their dot product must equal 0.

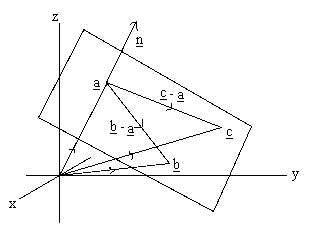
Using 3 points instead
Let a, b, c be the position vectors of 3 points in the plane. Then all we have to do to find the equation of the plane is construct a normal vector - then we can use this and any of the 3 points to find the equation as before.
The two vectors,
b - a (A to B)
c - a (A to C)
both lie in the plane, so if we take their cross product we find our normal vector:
n = (b - a) x (c - a)
So as before our equation for the plane consists of all vectors, r satisfying
(r - a) . n = 0
=>(r - a) . ((b - a) x (c - a)) = 0