By,
M. V. Vinod and M. Nikhil Chakravarthy,
Final Year BE ( Comp Sci ), NIE, Mysore.
1.Introduction
Unlike in Natural Languages where a sentence can take different meanings depending on the context, in computer evaluation there is no room for ambiguity. To evaluate an expression a parse tree is generated with the help of which the expression is evaluated. Unless this parse tree is unique, the computer cannot logically decide which tree to evaluate from. To make the parse tree unique, one uses parentheses. Basically the parentheses were used to eliminate ambiguity and to accommodate for overriding hierarchy of operators i.e. to evaluate a + or - before a * or /. The polish logician Jan Lukaseiwicz first introduced the polish (prefix) notation into mathematics for the evaluation of expressions. The advantage of such an expression over conventional ones was that there were no parentheses in the expression. It still took care of hierarchy of operators during evaluation and uniqueness of expression during generation of parse tree. For example in the conventional infix expression the format of the expression to be evaluated would be:
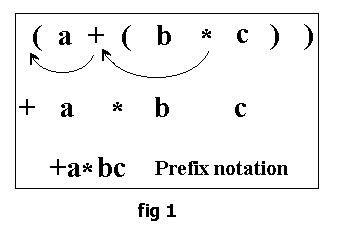
(a+(b*c))
The same expression in the prefix form would be of the form:
+a*bc
This is obtained by shifting the operators to the left of their nearest left parentheses and deleting the left and right parentheses in the given infix expression. The steps are as shown in fig1.

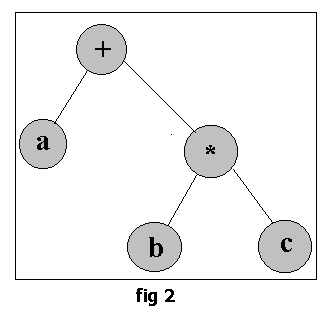
The parse tree generated by this expression would be as shown in fig 2.
Some of the features, which one notices on looking at this representation, are:

Note:
Even though the only difference in getting the prefix or postfix expressions is in shifting the operator to the left or to the right, the two expressions are not symmetric to each other.
2. Assumptions
For the sake of simplicity some assumptions are being made. They are as follows:
3.1 Conversion of Infix to Prefix notation
The steps involved are:
Push the operator into the operator stack, operand into the operand stack, ignoring left parentheses until a right parentheses is encountered. Then
Pop operand 2 from operand stack
Pop operand 1 from operand stack
Pop operator from operator stack
Concatenate operator and operand 1
Concatenate result with operand 2
Push result into the operand stack
This procedure is repeated until the end of the input string. The final result is obtained in the operand stack.
3.2 Conversion of Infix to Postfix notation
The steps involved are:
Write an operand onto the vector, push an operator into the stack, and ignore left parentheses until a right parenthesis is encountered. Then
Pop operator and write onto the vector.
This procedure is repeated until the end of the input string. The final result would be found in the vector.
4. Differences
As we have assumed the input infix expression to be a valid one and which is completely parenthesized so that the question of hierarchy of operators does not arise we can calculate the number of elements in each set i.e. operators, operands and parenthesis.
For a given infix expression like (a+(b*c)) if we were to denote the number of operands by x and number of operators by y and the number of parenthesis by z we can calculate the individual space taken up by each set. In the above case we see that:
x = 3, y = 2, z = 4
In general for a valid infix expression the number of operators is always one less then the number of operands i.e.
y = x - 1
Also since we are assuming the expression to be completely parenthesized to avoid the issue of hierarchy of operators it is logical to reason that for every operator there will be two parenthesis, one left and one right. Therefore
z = 2 * y
For a given input of length n
x+ y + z = n
we see that
Number of operands, x = ( n + 3 ) / 4
Number of operators, y = ( n - 1 ) / 4
Number of parenthesis, z = ( n - 1 ) / 2
Number of operators and operands, x + y = ( ( n + 3 ) / 4 ) + ( ( n - 1 ) / 4 )
Therefore x + y = ( n + 1 ) / 2
So if we were to use static allocation of memory we would have to reserve ( n + 1 ) / 2 characters for each element of the stack. In the case of postfix conversion the individual elements of the stack are only one character in length and the stack would need to contain (n -1) / 4 elements. So we see that conversion of infix to postfix is easier on both data structure manipulation and memory allocation when compared to that of prefix conversion.
6. Proposed Algorithm
If we were to give some thought over how one gets an prefix or postfix notation i.e. shifting the operator to the left or to the right we would likely assume that the two expressions for the same infix expression would be symmetric in nature i.e.
(a + b) infix
+ a b prefix
a b + post fix
but if we were to take an expression like
a b c + * postfix
we see this is not the case.
If while converting the infix expression to its corresponding prefix form, we were to look at the process in a mirror we would be seeing a conversion to postfix form as illustrated in fig 4.

If we were to view the postfix conversion in the normal view we would see the necessary prefix expression as shown in fig 5.

The implementation of this as an algorithm is as follows:
replace V[m] with a right parenthesis
Else if V[m] is a right parenthesis then
replace V[m] with a left parenthesis
End if
S[q] ß V[m]
Else if V[m] is an operator then push it into the operator stack.
9. Ignore Left parenthesis. 10. If the V[m] is a right parenthesis than pop operater1 from the operator stack :
operator1 ß operator at top of operator stack
q ß q + 1
S[q] ß operater1
End if
11. Reverse the vector S.
12. The postfix notation is found in the vector S and is of length (n+1)/2.
To further simplify the procedure we could feed the input vector in the reverse order. We would then have to interchange the roles of the left and right parenthesis. Further while storing the elements in the vector S we could place each element in its final resting-place using the addressing function as shown:
The Enhanced Performance Implementation is as follows:
S[q] ß V[m]
Else if V[m] is an operator then push it into the operator stack. 6. Ignore Right parenthesis. 7. If the V[m] is a Left parenthesis than
pop operator1 from the operator stack :
operator1 ß operator at top of operator stack
q ß q - 1
S[q] ß operater1
End if