A NEW ALGORITHM TO CONVERT INFIX TO PREFIX EXPRESSION.

      By,
       M. V. Vinod and M. Nikhil Chakravarthy, Final Year BE ( Comp Sci ), NIE, Mysore.

 1.Introduction

Unlike in Natural Languages where a sentence can take different meanings depending on the context, in computer evaluation there is no room for ambiguity. To evaluate an expression a parse tree is generated with the help of which the expression is evaluated. Unless this parse tree is unique, the computer cannot logically decide which tree to evaluate from. To make the parse tree unique, one uses parentheses. Basically the parentheses were used to eliminate ambiguity and to accommodate for overriding hierarchy of operators i.e. to evaluate a + or - before a * or /. The polish logician Jan Lukaseiwicz first introduced the polish (prefix) notation into mathematics for the evaluation of expressions. The advantage of such an expression over conventional ones was that there were no parentheses in the expression. It still took care of hierarchy of operators during evaluation and uniqueness of expression during generation of parse tree. For example in the conventional infix expression the format of the expression to be evaluated would be:

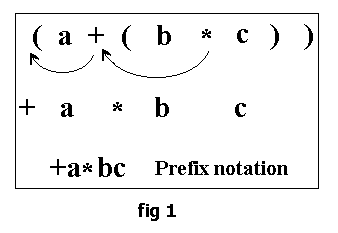
(a+(b*c))

The same expression in the prefix form would be of the form:

+a*bc

This is obtained by shifting the operators to the left of their nearest left parentheses and deleting the left and right parentheses in the given infix expression. The steps are as shown in fig1.

The parse tree generated by this expression would be as shown in fig 2.

 

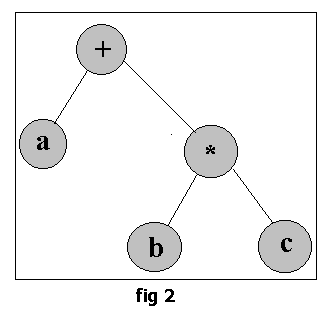
Some of the features, which one notices on looking at this representation, are:

  1. The operators (+, * etc) precede the operands (a..z, 0..9).
  2. The operands maintain the same order in the prefix expression as in the equivalent infix expression.
  3. There is no use of parentheses in the expression.
  4. Parentheses are not required to designate hierarchy of operators.
  5. There is no ambiguity in evaluation of expression.
Another form of expression or notation is the reverse polish or postfix representation. This is similar to the prefix notation and differs in the way that the operators are moved to the right of right parentheses that is nearest to them. The steps in obtaining postfix expression for the example considered earlier are shown in fig 3.

Note:

Even though the only difference in getting the prefix or postfix expressions is in shifting the operator to the left or to the right, the two expressions are not symmetric to each other.

2. Assumptions

For the sake of simplicity some assumptions are being made. They are as follows:

  1. The input Infix expression is in the form of a vector of known length.
  2. The Infix expression is a valid one and is completely parenthesized so that checking for hierarchy of operators does not come into picture.
  3. Operators allowed are of unit length i.e. +, -, *, /, ^ (a**b).
3. Standard Algorithms

3.1 Conversion of Infix to Prefix notation

The steps involved are:

Push the operator into the operator stack, operand into the operand stack, ignoring left parentheses until a right parentheses is encountered. Then

Pop operand 2 from operand stack

Pop operand 1 from operand stack

Pop operator from operator stack

Concatenate operator and operand 1

Concatenate result with operand 2

Push result into the operand stack

This procedure is repeated until the end of the input string. The final result is obtained in the operand stack.

3.2 Conversion of Infix to Postfix notation

The steps involved are:

Write an operand onto the vector, push an operator into the stack, and ignore left parentheses until a right parenthesis is encountered. Then

Pop operator and write onto the vector.

This procedure is repeated until the end of the input string. The final result would be found in the vector.

4. Differences

  1. In prefix notation the result is stored as a string and every time a string concatenation operation is performed the length of the string keeps increasing gradually during the execution of the loop where as in postfix notation the result is stored in a vector and there is no need for concatenation as the final location of an element can be obtained directly through addressing.
  2. In prefix notation there are two stacks one for the operand and one for the operator where as in postfix notation there is only one stack for operators.
  3. In prefix notation the length of the string in the operand stack keeps on increasing due to the concatenation of strings so if we were to use static allocation of memory then the length of the string to be reserved in memory for each element of the stack would be (n+1)/2 for a given input vector of length n.
  4. In postfix notation as the sequence of operands is the same as in the input vector they are directly assigned to the solution vector.
5. Memory Allocation

As we have assumed the input infix expression to be a valid one and which is completely parenthesized so that the question of hierarchy of operators does not arise we can calculate the number of elements in each set i.e. operators, operands and parenthesis.

For a given infix expression like (a+(b*c)) if we were to denote the number of operands by x and number of operators by y and the number of parenthesis by z we can calculate the individual space taken up by each set. In the above case we see that:

x = 3, y = 2, z = 4

In general for a valid infix expression the number of operators is always one less then the number of operands i.e.

y = x - 1

Also since we are assuming the expression to be completely parenthesized to avoid the issue of hierarchy of operators it is logical to reason that for every operator there will be two parenthesis, one left and one right. Therefore

z = 2 * y

For a given input of length n

x+ y + z = n

we see that

Number of operands, x = ( n + 3 ) / 4

Number of operators, y = ( n - 1 ) / 4

Number of parenthesis, z = ( n - 1 ) / 2

Number of operators and operands, x + y = ( ( n + 3 ) / 4 ) + ( ( n - 1 ) / 4 )

Therefore x + y = ( n + 1 ) / 2

So if we were to use static allocation of memory we would have to reserve ( n + 1 ) / 2 characters for each element of the stack. In the case of postfix conversion the individual elements of the stack are only one character in length and the stack would need to contain (n -1) / 4 elements. So we see that conversion of infix to postfix is easier on both data structure manipulation and memory allocation when compared to that of prefix conversion.

6. Proposed Algorithm

If we were to give some thought over how one gets an prefix or postfix notation i.e. shifting the operator to the left or to the right we would likely assume that the two expressions for the same infix expression would be symmetric in nature i.e.

(a + b) infix

+ a b prefix

a b + post fix

but if we were to take an expression like

( a * ( b + c ) ) infix * a + b c prefix

a b c + * postfix

we see this is not the case.

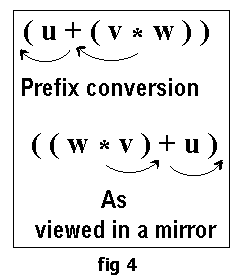
If while converting the infix expression to its corresponding prefix form, we were to look at the process in a mirror we would be seeing a conversion to postfix form as illustrated in fig 4.

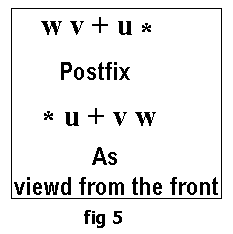
If we were to view the postfix conversion in the normal view we would see the necessary prefix expression as shown in fig 5.

The implementation of this as an algorithm is as follows:

  1. Accept n, V.
  2. Initialize q, vector S : S[(n+1)/2], q ß 0.
  3. Reverse the input vector V.
  4. Repeat step 5 varying m by 1 from 1 to n.
  5. If V[m] is a left parenthesis then

    6. replace V[m] with a right parenthesis

    Else if V[m] is a right parenthesis then

    replace V[m] with a left parenthesis

    End if

  6. Repeat steps 7 to 10 varying m from 1 incrementing by 1 until m>n.
  7. Read mth element of the input vector that is V[m].
  8. If V[m] is an operand then
q ß q + 1

S[q] ß V[m]

Else if V[m] is an operator then push it into the operator stack.

9. Ignore Left parenthesis. 10. If the V[m] is a right parenthesis than pop operater1 from the operator stack :

operator1 ß operator at top of operator stack

q ß q + 1

S[q] ß operater1

End if

11. Reverse the vector S.

12. The postfix notation is found in the vector S and is of length (n+1)/2.

  1. Performance Analysis
The steps 6 to 10 are the same as in the postfix algorithm. The steps 3 and 11 have (n / 2) comparisons and the step five takes 3(n -1) / 4 + (n +1) comparisons.

To further simplify the procedure we could feed the input vector in the reverse order. We would then have to interchange the roles of the left and right parenthesis. Further while storing the elements in the vector S we could place each element in its final resting-place using the addressing function as shown:

The Enhanced Performance Implementation is as follows:

  1. Accept n, V.
  2. Initialize q, vector S : S[(n+1)/2], q ß ((n+1)/2 )+1.
  3. Repeat steps 4 to 7 varying m from n incrementing by -1 until m<1.
  4. Read mth element of the input vector that is V[m].
  5. If V[m] is an operand then
q ß q – 1

S[q] ß V[m]

Else if V[m] is an operator then push it into the operator stack. 6. Ignore Right parenthesis. 7. If the V[m] is a Left parenthesis than

pop operator1 from the operator stack :

operator1 ß operator at top of operator stack

q ß q - 1

S[q] ß operater1

End if

  1. The postfix notation is found in the vector S and is of length (n+1)/2.

8. Conclusion

We have shown that reversing the string, interchanging left and right parenthesis, obtaining postfix, reversing again we would get a prefix expression. We can easily see that the converse would also apply i.e., reversing the string, interchange left and right parenthesis, obtaining prefix, reversing again we would get a postfix expression. So given a program to convert an infix expression to a prefix or postfix expression, the same algorithm can be used to obtain both postfix and prefix expression using the procedure explained.

9. Acknowledgements

The authors of this paper would like to thank Mr. K. Raghuveer, Lecturer, for his meticulous and through teaching on the subject of data structures. We would like to thank Dr. G. Raghavendra Rao, Systems Manager, for his guidance on the complexity and efficiency of computer algorithms. We would like to thank Dr. M. S. Shiva Kumar, Head, Department of computer science and engineering, N.I.E. Mysore, for providing the lab facility.

10. References

Top

Back To Home Page