As most of us already know, light travels in the form of radiation called electromagnetic waves. Since this is considered to be one of the physical laws of nature, Einstein stated his second postulate of the special theory of relativity:

So, let's go back to Bob and Tom at the train station. We now have a much faster train traveling at about 100 million m/s and, instead of throwing a baseball, Bob now has a flashlight which "throws" photons of light forward at about 300 million m/s. Now we've already been through this situation. The photons move at a speed of 300 million m/s relative to Bob, while Bob moves at a speed of 100 million m/s relative to Tom. So, to calculate the speed of the photons relative to Tom, we just have to add these numbers. The speed of the photons relative to Tom is 400 million m/s. However, that creates a problem. This directly contradicts Einstein's second postulate, which says that the speed of light in Tom's frame must be the same as in Bob's frame: 300 million m/s. So which is wrong: the Galilean relativity that we arrived at earlier, or Einstein's postulates? Well, many scientific experiments back up Einstein, so let's assume he's right and let's try to figure out what could be wrong with Galilean relativity.

Remember that the decision to add the velocities came fairly easily. After one second, a photon has moved 300 million meters ahead of Bob, and Bob has moved 100 million meters ahead of Tom. So the photon must move 400 million meters ahead of Tom during that second. There are only two ways that this can possibly not be 400 million m/s:

1. The 300 million meters, relative to Bob, is not really 300 million meters relative to Tom.
2. One second for Bob is not the same as one second for Tom.

As strange as each of these possibilities may sound, they are, in fact, both correct. The first effect is referred to as "length contraction" and the second effect is called "time dilation".

Length contraction is sometimes referred to as Lorentz contraction, or Lorentz-FitzGerald contraction. The mathematical formula for describing it was attained by Lorentz and Fitzgerald before Einstein, but Einstein was the first to fully understand its importance and embed it into a complete theory of relativity. The principle is this:

The length of an object in its own rest frame is called its "proper length". The proper length of a yardstick is one yard. When an object is moving quickly, its length will become shorter than its proper length. This contraction is not an illusion. Any accurate experiment we might contrive to measure the length of an object as it moves past us will reveal a shorter length than the object has at rest. The object doesn't just look shorter when it's moving. It is shorter, though only along the direction it's moving. However, for a reason which may not be clear at first, it would be realistically impossible to measure the actual contraction of an object. For example, let's say an object at rest is exactly one foot long when we measure it with a ruler. Now, we take the same one-foot object and measure it with the same ruler when it is moving at a speed near that of light. Measuring it would reveal that it is now shorter than a foot, right? Wrong. What you may not have realized is that the ruler would also have to be moving at the same speed as the object in order to measure it accurately. And what does that mean? Well, the length of the ruler has contracted as well . . . just as much as the object, in fact. So, even at incredibly high speeds, if we measure an object with a device which is moving at the same rate of speed, the object will appear to be the same length as it was when it was at rest. As you can see, actually measuring the length contraction of an object moving at such an incredible speed would be quite a daunting task for the scientific world to accomplish.

The effect called time dilation is similar to length contraction, and it works like this:

Sounds a bit confusing, doesn't it? Here's an illustration to help you understand this concept more easily:

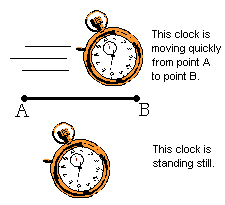
As you can see, we have two clocks. One is moving rapidly from point A to point B and the other is at rest. Either of these clocks can be used to measure the time it takes the first clock to travel from point A to point B. However, the two clocks will give different results. We can think of it this way. The two events we're talking about are the clock leaving point A, and the clock arriving at point B. In our frame (the frame of the lower clock which is at rest), these events take place at different points (A and B). However, let's look at this from the reference frame of the upper clock. From this point of view, the upper clock is at rest (anything is at rest from its own point of view) and the line containing the points A and B is rushing by from right to left. So, the two events, the departure of point A and the arrival of point B, both take place at the same point: the point where the clock sits! (The time measured by the upper clock is called the "proper time".) By the principle stated above, the lower clock will record a longer time than the upper clock as the upper clock moves from point A to point B.

A simpler, less exact way of stating this principle is to say that:

Time dilation is not just some wild idea conjured up in Einstein's imagination. Believe it or not, it has actually been verified experimentally. Perhaps the best example of this involves a subatomic particle called a muon. The muon is an unstable particle, which means that shortly after one is created, it decays into lighter particles. How long a muon takes to decay has been measured very precisely. Scientists have noticed that a muon moving close to the speed of light exists longer than a muon that is at rest or moving slowly. This is a relativistic effect. From the point of view of the moving muon it doesn't live any longer, because from its point of view, it is at rest. However, from the point of view of a scientist in the laboratory through which the muon moves, the lifetime of the muon is lengthened, or dilated. By the way, for more information about muons and other subatomic particles, try researching the subject of Quantum Mechanics.

• The Gamma Factor
• Back to Main Page