 |
|
||||||||||||||||||||
|
y = a(x - h)2 + k is the vertex form of the equation The vertex is at (h, k) The axis of symmetry is the vertical line x = h One of the graphs above has a vertex at (2, - 3) (h, k) Use the vertex form to write an equation of the parabola y =
a(x - h)2 + k use vertex for h and k y =
a(x - 2)2 + (- 3) Use coordinates of another point on the parabola for the x and y. (0, 1) 1=
a(0 - 2)2 + (- 3) Simplify & solve for a 1= a(- 2)2 + (- 3) +3 + 3 4=
a(- 2)2 4=
4a divide both
sides by 4 1 = a Write the vertex form again, subbing in a, h, k. leave xx and yy y =
a(x - h)2 + k y =
1 (x - 2)2 - 3 y =
(x - 2)2 - 3 Graphing using the vertex form y =
- 2(x + 3)2 + 8 Since the number front of the
parenthesis is 2 , you know that the U is turned down and that it is narrow. The vertex x is OPPOSITE the pos. 3 the vertex y is the same as the constant 8 vertex is ( - 3, 8) The axis of symmetry is x = - 3 It is always good to know where the graph crosses the axis, so let x = 0 y =
- 2(x + 3)2 + 8 y =
- 2(0 + 3)2 + 8 y =
- 2(3)2 + 8 y =
- 2(9) + 8 y =
- 18 + 8 y =
- 10 Plot (0, - 10) That is 3 right of the axis of symmetry, so, you know there is a mirror point 3 left of the axis -3 + -3 = -6 Plot (- 6, - 10) let y = 0, sub in y = - 2(x + 3)2 + 8 0 = - 2(x + 3)2 + 8 0 = - 2(x2+ 6x + 9) + 8 0 = - 2x2+ -12x + -18 + 8 0 = - 2x2+ -12x + -10 -2 - 2
- 2 - 2 0 =
x2+ 6x + 5 0 = (x +5)(x +1) x +5= 0
x +1 = 0 - 5 - 5
-1 -1 x
= -5 x
= -1 Plot (-5, 0) and (-1, 0) 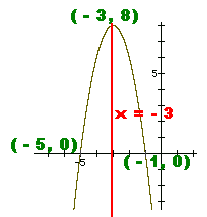 Enter supporting content here
|
|||||