Given the latitudes and longitudes of two points on the surface of a sphere
which happens to have a radius of 6369 km, how do you determine the
shortest distance between them if you are constrained to travel along the
surface of the sphere?
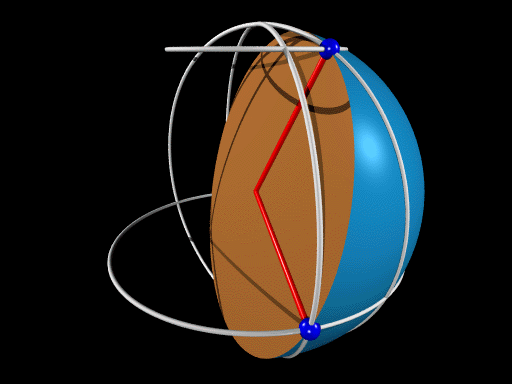
The above diagram tries to show the two locations as small blue spheres, the red
lines being their position vectors from the centre of the sphere. (Their lines
of latitudes and longitudes are represented by white circles). From this you
can see that the shortest distance between the two points is given by the length
of an arc of a circle concentric with the sphere and with the same radius as the
sphere. Knowing that arc length is just the product of the radius and the angle
subtended at the centre of the circle, you can use your knowledge of spherical
polar coordinates and the dot product to find this distance.
Challenge: Find the distance between London and New York,
N.BThe equator is the line of 0 latitude, the north pole has latitude
90 N, and the south pole 90 S. The Greenwich Meridian has longitude 0 and longitude
extends up to 180 E (which is the same as 180 W) on the other side of the Earth.
| London | Lat: 52 N | Long: 0 |
| New York | Lat: 41 N | Long: 73 W |