Annex 2
A simplified picture of the demand and supply situation for telecom in India
This Annex provides a simple picture of the demand and supply situation in India to illustrate some of the conditions prevailing in the market. The main points that emerge here are:
(a) A simplified picture of demand for telecom services in India
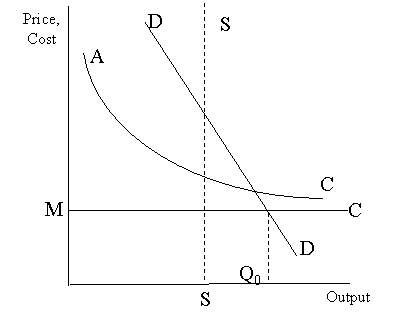
The Figure below shows a simplified picture of the demand and cost situation relevant to telecom pricing. DD is the demand curve for a basic telecom service, MC is the marginal cost curve, and AC is the average cost curve. For simplification, marginal costs are shown to be the same for each unit of output. Since fixed costs do not change with a change in the output level, the average total costs (comprising average fixed and marginal costs) will be above marginal costs, but declining.

In the Figure above, the level of output Q0 is the level at which price is equal to marginal cost (i.e., the point of intersection of the demand curve and the marginal cost curve). It is evident that the price does not cover costs at that level because the average cost is above the price level. The Ramsey rule suggests the extent to which the price should be increased to obtain the revenue that would cover costs and provide an adequate return. The Ramsey rule requires that the prices be those given by the demand curve, i.e. there should not be any constraint for the customer to be operating on the demand curve.
In the Indian situation, however, there is likely to be a capacity constraint and thus the customers are unlikely to be on the demand curve. The capacity constraint in India arises for two reasons. One, the subscribers linked up to the network face congestion and are thus not able to make as many completed calls as they desire. Second, the existing network does not satisfy the demand of all those wanting to be linked up to the network. The first type of constraint (i.e. congestion) implies that the supply constraint shown by SS is the operating schedule for the subscribers.
Some tentative conclusions could be drawn from this discussion. Due to the prevailing excess demand, a change in price will not alter overall demand as long as there is excess demand. In such a situation, the price could be increased till the price is high enough to reach the demand schedule, i.e. till the point where the supply equals demand. This does not mean that certain subscribers will not reduce their demand, but that the reduction in demand will be compensated by the prevailing excess demand filling the gap till the price becomes so high that excess demand itself becomes zero.
Excess demand also implies that a high price could be charged for those telecom services for which subscribers are willing to pay a high price, i.e. service for which the price shown by the demand curve is high at a given level of the supply constraint. However, it is not clear what this price level should be, because the demand curve is not easy to determine.
(b) Excess Demand -- Congestion

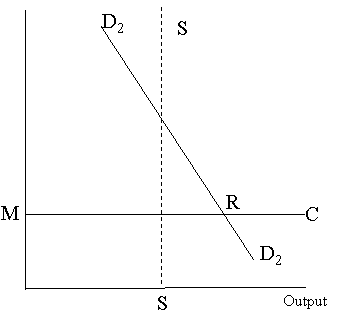
Once again, MC is the marginal cost curve and DD is the demand curve. The congestion in the network due to a capacity constraint is reflected by the vertical line SS. The output Q1 corresponding to the vertical line shows the supply beyond which the volume of traffic cannot be increased (Technically, with increasing congestion, the vertical line could move to the left, thus showing decreasing capability of the network with a rise in congestion).
The fact that there is a congestion is diagrammatically illustrated by the fact that the actual demand for the product is more than the capacity. With congestion, the customer is somewhere on the vertical line SS and not on the demand curve. The excess demand is shown by the horizontal distance between the vertical line SS and the demand curve. Therefore, the actual price is somewhere lower than P1.
For a proper implementation of the Ramsey rule, the point of reference from where the movement for mark-up has to occur is the point where the demand curve intersects the marginal cost curve, i.e. point R in the diagram above. In a situation with congestion, the starting point itself is away from the Ramsey reference point, and the position of this starting point is dictated by the available capacity. Furthermore, the position of this capacity constraint for different types of services (or demand) might be different, and it is highly unlikely that these constraints are positioned in such a way that the Ramsey rule for mark-up could be satisfied for different services.
The fact that the price is above marginal cost means that some mark-up already exists. Any change in the mark-up (due to a change in price) will not affect the level of demand as long as the customers face a capacity constraint, i.e. as long as they are on the vertical line SS above. Thus, in effect, the elasticity of demand for each service with a capacity constraint is the same, i.e. it is equal to zero on SS.
(c) Overall excess demand is a combination of different situations

The fact that there is overall excess demand due to congestion does not mean that such congestion operates everywhere. Thus, the situation would comprise those who do not face any supply constraints and others who face a supply constraint in certain parts of the country. This is shown by the two demand curves above, D1D1 and D2D2. Only D2D2 is subject to a supply constraint, and thus a change in price will affect the overall level of demand of those in situation D1D1 and not of those in situation D2D2. However, the presence of a supply constraint does reduce the elasticity (or responsiveness) of the overall demand for the telecom service.
(d) Excess Demand For Telephone Connections
There is considerable excess demand for telephone connections in India, and this demand is expected to rise sharply in the near future. The Department of Telecommunications has estimated that in the next five years, demand for telephones is likely to more than double. While capacity extension will continue to try to cater to this demand, this situation adds to the difficulty created by the abovementioned capacity constraint in using the demand situation in India to assess the telecom price or the mark-up.

In the Figure above, an expansion of capacity is shown by a rightward shift of the vertical line S1S1 to SS. This capacity expansion results in meeting the excess demand of those who were on the waiting list. The waiting list is shown by the difference between the demand curves D1D1 to D2D2. To this must be added the increase in demand over time. Adding these would give us the new demand curve as D4D4. The effect of these changes on the excess demand situation (or on congestion) would depend on the extent of the change in capacity and the extent of prevailing excess demand and the increase in demand over time. If those demanding a link-up with the network are not provided the link-up, then the actual demand at D3D3 will be to the left of D4D4. The difference between D3D3 and D4D4 shows the demand in waiting. Moreover, if there continues to be congestion for those linked up to the network, we are again in the same situation as the one discussed earlier, i.e. the consumer is likely to be on the supply constraint and not on the demand curve.
Even if the customer is not subject to the supply constraint, it may not be feasible to apply the Ramsey rule as long as the desired price is to the right side of the supply constraint. Moreover, when the link to the network is increasing as rapidly as 20 per cent per annum, and excess demand still continues to prevail, it is very difficult to estimate demand characteristics accurately or to use the demand curve for pricing telecom.
(e) When the Price Declines
With a capacity constraint, the decline in price would take place without any change in the level of existing demand. On the other hand, if there is no capacity constraint, then the fall in price would take place along the demand curve. In this case, the short-term effect on revenue would depend on the elasticity of demand.
However, if the price decline increases demand to such an extent that the capacity constraint becomes binding again, then the elasticity of demand becomes irrelevant in calculating the change in revenue. This is shown in the diagram below. The staring point is price P1, and two different demand curves are considered, with different elasticities of demand. At price P2, the supply constraint becomes binding for demand curve D1D1, and at price P3 it becomes binding for demand curve D2D2. At prices lower than P3, the comparison of the old and the new levels of revenue does not depend on the elasticities of the demand curves.

back to Annex 1
forward to Annex 3
return to india_gii's home page