1. Attended and presented a paper in Tenth Canadian Congress of Applied Mechanics
(CANCAM-85)
Venue:
A campus view of
Date: June 2-7, 1985
Paper Title: Analysis of a Line Contact Problem Using Scattered-Light Photoelasticity
Abstract of Paper
A large
number of practical problems are not amenable to the theoretical analysis.
Consequently, the experimental methods in stress analysis, such as
photoelasticity are assuming greater prominence in engineering design. In
conventional photoelastic processes, general three-dimensional models are
tested under stress frozen conditions, i.e., the stresses are locked in the
model at the critical temperature of model material. For stress-frozen model at
critical temperature, the elastic constants (E and u, the Young’s modulus and Poisson’s
ratio) which affect the stress distribution [1] are entirely different from
those of the prototype. Similarity in stress distribution can be obtained by
suitable adjustment of load with respect to Young’s Moduli, but no such
adjustment is possible to compensate for the differences in Poisson’s ratio.
The objectives of the present investigations are:
1.
to determine theoretically (i.e., based on
Thomas and Hoersch solution [1]) the influence of Poisson’s ratio on stress
components in a line contact problem and experimentally verify it; and
2.
to compare
theoretical solutions with experimental results and to find to what extent the
theory is applicable to finite bodies.
For purposes
of investigation, tests were conducted on two sets of models (cylinders pressed
against rectangular blocks under normal loading conditions). Figure 1 shows the
geometry of the models that were investigated. One set of the models was
subjected to live loads at room temperature conditions and investigated. A
second set of geometrically similar models was subjected to the conventional
stress freezing process and later investigated. Table 1 gives the details
regarding applied loads and properties of the material.
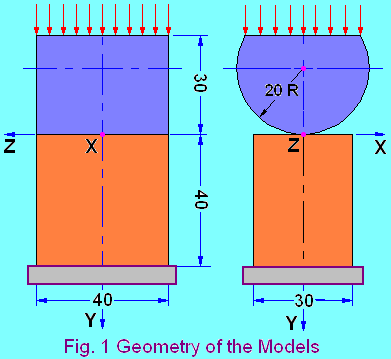
Table 1: Material properties and applied loads
|
Details |
LL
model |
SF
model |
|
Normal
load transmitted through the
line of contact (kgf) |
282.0 |
8.5 |
|
Young’s
Modulus (kgf/cm2) |
28800.0 |
870.0 |
|
Poisson’s
Ratio |
0.31 |
0.49 |
|
Material
fringe value (kgf/fringe/cm) (for
the He-Ne laser, λ = 6328 A0) |
13.38 |
0.412 |
The models are made of hot-set araldite
material composed of CY-230 resin and HT-901 hardener taken in proportions
100:45 by weight.
The ratio of the load applied to the
live-load and stress-frozen model was kept equal to the ratio of their Young’s
moduli so that the variation in stresses due to a change in Poisson’s ratio
alone could be studied.
In
the experimental investigations, the techniques of scattered-light photoelastic
were used advantageously since investigations can be carried out (in a
completely non-destructive manner) on models under live loads as well as on
models with stresses locked-in. The
currently available scattered-light techniques completely take care of the problem
of rotation of secondary principal axes along the light path using the concept
of optically equivalent model and enable one to determine the associated
photoelastic parameters along the light path using which one can calculate the
corresponding secondary principal stress differences and their axis [2]. A
photographic view of the scattered-light polariscope is shown in Fig. 2.

Fig. 2 Photographic view of scattered-light
polariscope
The
theoretical and experimental results were compared to study the influence of
Poisson’s ratio on stress distributions near the area of contact. The results
also revel the extent to which the theoretical
solution developed for the infinite medium is applicable to finite bodies.
The
accuracy of the results obtained shows the potentials of scattered-light
technique as a powerful non-destructive experimental tool in the investigation
of interior stresses in three-dimensional bodies.
1.
Thomas, H.R. and Hoersch, V.A., ‘Stress due to Pressure
of one Elastic Solid upon Another’,
2.
Srinath, L.S. Godbole, P.B. and Keshavan S.Y., ‘A
New Scattered Light Method to Determine Stresses near an Interior Crack-tip’,
Proc., IUTAM Symp. On Optical Methods Mech., Vol.2, pp 775-781, (1962).
|
Appointment |
Research Interests |
Publications
|
Positions Held |
Academic
Experience
| Students |
Citations |
Courses |
|
My Alma mater |
My Teachers |
Foreign Assignments |
My Friends |
My Colleagues
| My Family |
|
Route Map to my Residence (RMV Clusters) |