 | 複底.殘形.美學殘形美學與國畫 | 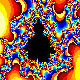 |
 | 複底.殘形.美學殘形美學與國畫 |  |
回溯到我們最初選擇這個研究方向的動機,是在數學圈雜誌上看到 幾幅「殘形」開始一一這可說是我們第一次看到殘形。這些殘形 所呈現出來無窮盡的玄機,牢牢地吸住了我們的目光。由於 這一次純粹美感的接觸,引發了我們與生俱來的好奇心,於是進而去探 索其中深藏的數學上的美。在整個研究過程中,隨著理論方面的日益充實,涵蓋範圍的囗漸拓 展,我們發現了許多意想不到的殘形,令人目眩神馳。這些殘形圖案常 常給我們許多靈感與啟示。
最重要的,這些五花入門的圖形,大大地沖淡了本研究在數學理論 上的生硬感,使我們的作品無形中更加搶眼。就算是外行人,不看理論 上的成果,光欣賞我們的圖形,也會深受震撼的。
在研究草創階段,我們選取的基底還在複整數系中,digit集仍侷限於自然digit集,後來,由於突破性的推 廣:以方陣為基底,一下子產生無窮多的變化,各種殘形紛紛出籠,令我們目不暇接。 這種殘形的美可分成兩類 : 第一種是邊界上的殘形,如 b=1+i,我們注目的焦點在於它的邊界曲線(不是普通一維的線), 所表現出來的內在位似。第二種美感來自整個殘形的殘缺斑斕、疏落有 致的美。第一種殘形其維數為2,然而其邊界曲線的維數則介於1與2 之間,第二種殘形是無窮多個點散置於平面上,其維數D介於O與2之間 ,也就是說,它是一種介於點與平面間的怪物。
關於邊界曲線的美,我們可以發現,維數大的曲線,看起來相當崎嶇 ;維數小的曲線,則平滑得多,以地理學的術語來說,像岩岸的曲線, 具有起伏劇烈的美,而屬於沙岸的曲線,則具有局部上玲瓏精緻的凹凸 現象,看來相當可愛。總而言之,殘形之所以美,正因為它具有殘形獨具的「缺陷美」,而這種美,在殘形維數適中(不接近整 數)的情形下最明顯。
離散的殘形,情形更有所不同。這些殘形的美,可以一言以蔽之:疏落有致。
我們發現這些殘形與國畫山水中的筆法有神似之處。像國畫筆法中 的山石皺法——大、小斧劈皺、披麻皺、荷葉皺等等,或是樹葉的點法 :介字點等等,以及浪花、沙洲的筆法,在我們用電腦所畫的殘形圖案中,都可 以找到一些痕跡。
 |  |
介字點
( 3 -1 )
b = ( )
( 1 3 )
| 山石皴法
( 2 -1 )
b = ( )
( 1 3 )
|
這是國畫中特別注重運用毛筆的皺擦,以及墨色的乾濕濃淡變化,才能
造成殘形獨具的風格——像皺法中呈現出來有如「飛白」的效果,細部
有疏密不一的墨跡,即具有殘形的特色。又例如山石邊緣因為點苔或濕
筆渲染所呈現出來毛絨絨的效果,使其邊緣的維數略大於 1。此外樹葉
的點法也有類似的效果。
例如李唐的「萬壑松風圖」上方的樹頂端即呈
現出不同維數的殘形,尤其右方的樹葉與b=1+i的殘形在局部上幾無二致。另外
范寬「谿山行旅圖」的樹叢也是很典型的殘形,其中上方的樹叢邊緣
的維數小於中下方樹叢邊界的維數。此外,郭熙的「早春圖」整個給人
一種奇特的感受,而畫中的樹邊界維數出奇的大,幾乎接近2維,是故
呈現突出的風格。郭熙畫山石如亂雲,這兩者都是殘形!(註)
國畫把墨色的變化發揮到了極致,是西洋繪畫所 難望其項背的,或許這殘形的美,也是中國山水畫能昂然卓立於世界眾 多畫派中間而歷久不墜的一個鮮為人知的原因吧。
在殘形世界中,有許多是常常看到,俯拾可得的,但也有許多是 人們不熟悉的,抽象但美麗的圖案,假如讀者有興趣,可以嘗試運用不 同的基底及數位集來畫,讓電腦充分發揮計算與繪圖的長處。
當然,「殘形雕塑」也是另一個有待探索的方向,我們到現在為止 ,尚未做出一個立體的殘形。立體的殘形必須要以3X3的矩陣為基底 ,其變化也是無窮盡的,但是在製作上有技術方面的困難。
註:「郭熙畫山水,石如鬼面,樹如鷹爪。山的皴法多 作「亂雲皴」又名「雲頭皴」。這種皴法是有人見到一片片的夏天浮雲,看上去好像是曾巒奇峰的樣子,於是仿照雲頭的形 狀,創出了雲頭皴。」引自http://www.hwh.edu.tw/~draw/